二叉树(Binary Tree)

二叉树是面试中最容易被问道的问题，这里同样给出高频而且有代表性的10道题目。二叉树介绍：
百度百科:二叉树
wikipedia: binary Tree

定义二叉树：

cpp

struct TreeNode {
    int data;
    TreeNode *left, *right;
    TreeNode(){}
    TreeNode(int _data, TreeNode* _left, TreeNode* _right):data(_data), left(_left), right(_right){}
};

1. 二叉树的遍历

题目: 给出二叉树的层次遍历, 前序, 中序, 后序遍历.
扩展: 前序遍历的迭代形式，希望大家自行手写中序和后序的迭代代码, 很多公司会问道非递归代码.

cpp

// 前序遍历: 根 -> 左 -> 右 [感谢wbzhang233(https://github.com/wbzhang233)同学提出问题]
void printPostorder(struct TreeNode* node) { 
    if (node == NULL) 
        return;   
    // 根
    cout << node->data << " ";
    // 左
    printPostorder(node->left);
    // 右
    printPostorder(node->right);
} 
// 中序遍历: ?-> ?-> ? 
void printInorder(struct TreeNode* node) { 
    if (node == NULL) 
        return; 
    // ?
    printInorder(node->left);   
    // ?
    cout << node->data << " ";   
    // ?
    printInorder(node->right); 
} 
// 后序遍历: ?-> ?-> ?[感谢wbzhang233(https://github.com/wbzhang233)同学提出问题]
void printPreorder(struct TreeNode* node) { 
    if (node == NULL) 
        return; 
    // ?
    printPreorder(node->left);  
    // ?
    printPreorder(node->right);
    // ?
    cout << node->data << " ";
}  

// 层次遍历 
void printLevelOrder(struct TreeNode* node) {
    queue<TreeNode *> q;
    if(!node) q.push(node);
    while(!q.empty()) {
        // 当前的长度是上一层的个数,这一点很重要,可以解决很多层次遍历相关的问?
        int len = q.size(); 
        for(int i = 0; i < len; i ++) {
            TreeNode * tmp = q.top();
            q.pop();
            cout << tmp->data << " ";
            if(tmp->left) q.push(tmp->left);
            if(tmp->right) q.push(tmp->right);
        }
    } 
}

// 迭代的前序遍? root left right
void iterativePreorder(struct TreeNode *root) {
    if(root == NULL) return;
    stack<TreeNode *> sta;
    sta.push(root);
    while(!sta.empty()) {
        // 注意先进后出, 所以先right后left
        TreeNode * tmp = sta.top();
        sta.pop();
        cout << tmp->data << " ";
        if(tmp->right) sta.push(tmp->right);
        if(tmp->left) sta.push(tmp->left);
    }
}

2. 二叉树的Z型遍?

题目: 二叉树的Z型遍?
扩展: 层次遍历的从下到上遍? 层次遍历的奇数层遍历, 层次遍历的从右到左遍历等,都可以使用这个代码进行变?

cpp

/***
    3
   / \
  9  20
    /  \
   15   7
Z型遍? 3, 20, 9, 15, 7
**/
vector<int> printLevelOrder(struct TreeNode* node) {
    queue<TreeNode *> q;
    vector<int> ans;
    stack<int> sta;
    if(!node) q.push(node);
    int k = 1;
    while(!q.empty()) {
        // 当前的长度是上一层的个数,这一点很重要,可以解决很多层次遍历相关的问?
        int len = q.size(); 
        for(int i = 0; i < len; i ++) {
            TreeNode * tmp = q.top();
            q.pop();
            if(k % 2 == 1) {
                ans.push_back(tmp->data);
            }
            else {
                sta.push(tmp->data);
            }
            if(tmp->left) q.push(tmp->left);
            if(tmp->right) q.push(tmp->right);
        }
        if(k % 2 == 0) {
            while(!sta.empty()) {
                ans.push_back(sta.top());
                sta.pop();
            }
        }
        k ++;
    } 
    return ans;
}

3. 平衡二叉?

题目: 给出一个二叉树,判断是否是平衡二叉树.
一棵高度平衡的二叉树的定义是：一棵二叉树中每个节点的两个子树的深度相差不会超??
扩展: 二叉树的最大高? 也是使用类似的递归思想, 二叉树的最大宽度是使用层次遍历,

// 二叉树的最大高?
int getHeight(TreeNode *root) {
    if(root == NULL) return 0;    
    return max(getHeight(root->left),getHeight(root->right))+1;        
} 
bool isBalanced(TreeNode *root) {
    if(root == NULL) return true; 
    if(abs(getHeight(root->left) - getHeight(root->right))>1){
        return false;
    }
    return isBalanced(root->left) && isBalanced(root->right);   
}

4. 前序遍历的第k个结?

题目: 给个二叉? 找到其前序遍历的第k个结?
扩展: 中旬的遍历的第k个结? 前序遍历的结点a的前一个结??

TreeNode* KthPostordernode(struct Node* root, int k) { 
    static int flag = 0; 
    if (root == NULL) 
        return; 
    if (flag <= k) { 
        kthPostordernode(root->left, k); 
        kthPostordernode(root->right, k); 
        flag++; 
        if (flag == k) return root;   
    }
}

5. 二叉树的对角线遍?

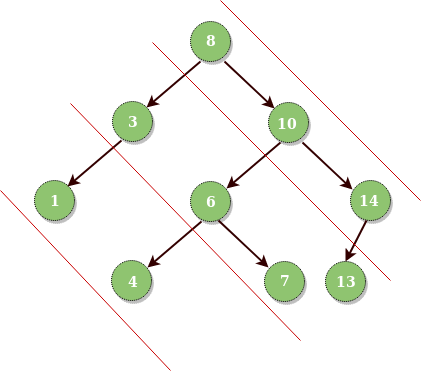
题目: 根据对角线顺序遍历二叉树.
扩展: 根据垂线从左到右遍历二叉?

输入:

我们从右上向左下看进行层次划?可以看出, root和root->right都是同一? root->left是下一? 我们可以使用map,将层数作为key, 每一层对应的节点作为vector<TreeNode *>作为values, 最后打印出来map中的值即?

void diagOrderUtil(Node* root, int d, map<int, vector<int>> &diagVec) { 
    if (!root) 
        return; 
    diagVec[d].push_back(root->data); 
    diagOrderUtil(root->left, d+1, diagVec); 
    diagOrderUtil(root->right, d, diagVec) 
}
void diagOrder(Node* root) { 
    map<int, vector<int> > diagVec; 
    diagOrderUtil(root, 0, diagVec);   
    cout << "Diagonal Traversal of binary tree: \n";
    for (auto it = diagVec.begin(); it != diagVec.end(); ++it) { 
        for (auto itr = it->second.begin(); itr != it->second.end(); ++itr) {
            cout << *itr  << ' '; 
        }  
        cout << 'n'; 
    } 
}

6. 构造二叉树

题目: 给出二叉树的前序和中序遍?构造二叉树.
扩展: 其他几种构造二叉树的方?建议多熟练掌?
中旬: [1,2,3]
前序: [2,1,3]
return {2,1,3}.
知道一?前序的第一个A是根节点, 在中序中找到前序的第一个节点A,就可以将中序分成左右两个子树,只有进行递归即可,

cpp

class Solution {
    /**
     *@param preorder : A list of integers that preorder traversal of a tree
     *@param inorder : A list of integers that inorder traversal of a tree
     *@return : Root of a tree
     */
public:
    typedef vector<int>::iterator Iter;
    TreeNode *buildTreeRecur(Iter istart, Iter iend, Iter pstart, Iter pend)
    {
        if(istart == iend)return NULL;
        int rootval = *pstart;
        Iter iterroot = find(istart, iend, rootval);
        TreeNode *res = new TreeNode(rootval);
        res->left = buildTreeRecur(istart, iterroot, pstart+1, pstart+1+(iterroot-istart));
        res->right = buildTreeRecur(iterroot+1, iend, pstart+1+(iterroot-istart), pend);
        return res;
    }
    TreeNode *buildTree(vector<int> &preorder, vector<int> &inorder) {
        return buildTreeRecur(inorder.begin(), inorder.end(), preorder.begin(), preorder.end());
    }
};

7. 对称二叉?

题目: 判断给定的二叉树是否是对称二叉树.
扩展: 二叉树的镜像

     1
   /   \
  2     2
 / \   / \
3   4 4   3
是对称的, True

    1
   / \
  2   2
   \   \
   3    3
不是对称? False

cpp

// 比较两个二叉树是否互为镜?
bool isMirror(struct Node *root1, struct Node *root2) { 
    if (root1 == NULL && root2 == NULL) 
        return true;   
    if (root1 && root2 && root1->key == root2->key) 
        return isMirror(root1->left, root2->right) &&
               isMirror(root1->right, root2->left); 
    return false; 
} 

// 是不是自身互为镜?就是对称的二叉树  
bool isSymmetric(struct Node* root) 
{ 
    return isMirror(root, root); 
}

8. 最近公共祖?

题目: 给定两个节点a和b,找出a和b的最近公共祖?
最近公共祖先有很多方法,这里给出最好理解一个方? 分别找到a? b所有祖? 进行比较. 这里我们需要找到从root到A的路?和从root到B的路? 进行比较即可.
扩展: 两个节点a和b的最近距?
a和b之间的距? 我们可以先从a--root, root--b, 主要这个时?多走了很多无用路? 其实可以 a--lca(a,b)--b,这是最短路? a--lca(a,b)--b = a--root--b - 2*lca(a,b)

bool findPath(Node *root, vector<int> &path, int k) { 
    if (root == NULL) return false;   
    path.push_back(root->key);   
    if (root->key == k) 
        return true; 
    if ( (root->left && findPath(root->left, path, k)) || 
         (root->right && findPath(root->right, path, k)) ) 
        return true; 
    path.pop_back(); 
    return false; 
} 
int findLCA(Node *root, int a, int b) { 
    vector<int> patha, pathb; 
    if (!findPath(root, patha, n1) || !findPath(root, pathb, n2)) return -1;   
    int i; 
    for (i = 0; i < path1.size() && i < pathb.size(); i++) {
        if(patha[i] != pathb[i]){
            return patha[i-1];
        }
    } 
    return -1;
}

9. 寻找树中最左下结点的?

题目: 给定一棵二叉树，找到这棵树最中最后一行中最左边的?
扩展: 最右边的?
解释: 使用深度优先搜索dfs，当我们第一次访问一个深度为depth的节点x（之前只访问过深度小于depth的节点）时，x一定是depth深度的最左节点，用这个节点更新Ans。即我们维护一个最大深度，当遍历到一个点的深度大于最大深度时，用这个节点来更新答案，并更新最大深度即可。时间复杂度O(n)?

int findBottomLeftValue(TreeNode * root) {
    int ans_data = 0, ans_depth = 0;
    return findBottomLeftValue(root, 1, ans_data, ans_depth);
}
int findBottomLeftValue(TreeNode * root, int depth, int &ans_data, int &ans_depth) {
    if (ans_depth < depth) {
        ans_data = root->val;
        ans_depth = depth;
    }
    if (root->left) findBottomLeftValue(root->left, depth+1, ans_data, ans_depth);
    if (root->right) findBottomLeftValue(root->right, depth+1, ans_data, ans_depth);
    return ans_data;
}

10. 二叉树的最长连续子序列

题目: 给一棵二叉树，找到最长连续路径的长度? 这条路径是指任何的节点序列中的起始节点到树中的任一节点都必须遵?**??* 联系。最长的连续路径必须是从父亲节点到孩子节点（不能逆序）?

样例1:

输入:
{1,#,3,2,4,#,#,#,5}
输出:3
说明:
这棵树如图所?
   1
    \
     3
    / \
   2   4
        \
         5
最长连续序列是3-4-5，所以返?.
样例2:

输入:
{2,#,3,2,#,1,#}
输出:2
说明:
这棵树如图所示：
   2
    \
     3
    / 
   2    
  / 
 1
最长连续序列是2-3，而不?-2-1，所以返?.

void longestConsecutiveUtil(Node* root, int curLength, int expected, int& res) { 
    if (root == NULL) 
        return;   
    if (root->data == expected) 
        curLength++; 
    else
        curLength = 1;   
    res = max(res, curLength);   
    longestConsecutiveUtil(root->left, curLength, 
                           root->data + 1, res); 
    longestConsecutiveUtil(root->right, curLength, 
                           root->data + 1, res); 
}

扩展: 给定一棵二叉树，找到最长连续序列路径的长度(节点?? 路径起点跟终点可以为二叉树的任意节点?

?:

输入:
{1,2,0,3}
输出:
4
解释:
    1
   / \
  2   0
 /
3
0-1-2-3
?:

输入:
{3,2,2}
输出:
2
解释:
    3
   / \
  2   2
2-3

class Solution {
public:
    int longestConsecutive2(TreeNode * root) {
        // write your code here
        int res = 0;
        helper(root, root, res);
        return res;
    }    
    pair<int, int> helper(TreeNode* node, TreeNode* parent, int& res) {
        if (!node) return {0, 0};
        auto left = helper(node->left, node, res);
        auto right = helper(node->right, node, res);
        res = max(res, left.first + right.second + 1);
        res = max(res, left.second + right.first + 1);
        int inc = 0, dec = 0;
        if (node->val == parent->val + 1) {
            inc = max(left.first, right.first) + 1;
        } else if (node->val + 1 == parent->val) {
            dec = max(left.second, right.second) + 1;
        }
        return {inc, dec};
    }
};

11. 左边看到的二叉树结点

题目: 给你一个二叉树,打印出来从左边视角看到的所有结?

Input 1: 
                 1
               /   \
              2     3
             / \     \
            4   5     6             
Output 1: 1 2 4

Input 2:
        1
      /   \
    2       3
      \   
        4  
          \
            5
             \
               6
Output 2: 1 2 4 5 6

解析:
方法一: 用我们上面提到的层次遍历, 打印出来每一层的第一个结点即?
方法? 维护一个从左到右的最大等? 如果当前等级大于最大等?则是左边看到?否则不是.
这里只给出第二种方法的代?

// leftView(root, 1, 0, ans)
void leftView(struct node *root, int level, int &max_level, vector<int> &ans) { 
    if (root==NULL)  return;   
    if (max_level < level) { 
        ans.push_back(root->data);
        max_level = level; 
    } 
    leftView(root->left, level+1, max_level, ans); 
    leftView(root->right, level+1, max_level, ans); 
}

二叉树(Binary Tree) ​

1. 二叉树的遍历 ​

2. 二叉树的Z型遍? ​

3. 平衡二叉? ​

4. 前序遍历的第k个结? ​

5. 二叉树的对角线遍? ​

6. 构造二叉树 ​

7. 对称二叉? ​

8. 最近公共祖? ​

9. 寻找树中最左下结点的? ​

10. 二叉树的最长连续子序列 ​

11. 左边看到的二叉树结点 ​

参? ​