Adaboost 算法介绍

1. 集成学习

集成学习（ensemble learning）通过构建并结合多个学习器（learner）来完成学习任务，通常可获得比单一学习器更良好的泛化性能（特别是在集成弱学习器（weak learner）时）。

目前集成学习主要分为2大类：

一类是以bagging、Random Forest等算法为代表的，各个学习器之间相互独立、可同时生成的并行化方法；

一类是以boosting、Adaboost等算法为代表的，个体学习器是串行序列化生成的、具有依赖关系，它试图不断增强单个学习器的学习能力。

2. Adaboost 算法详解

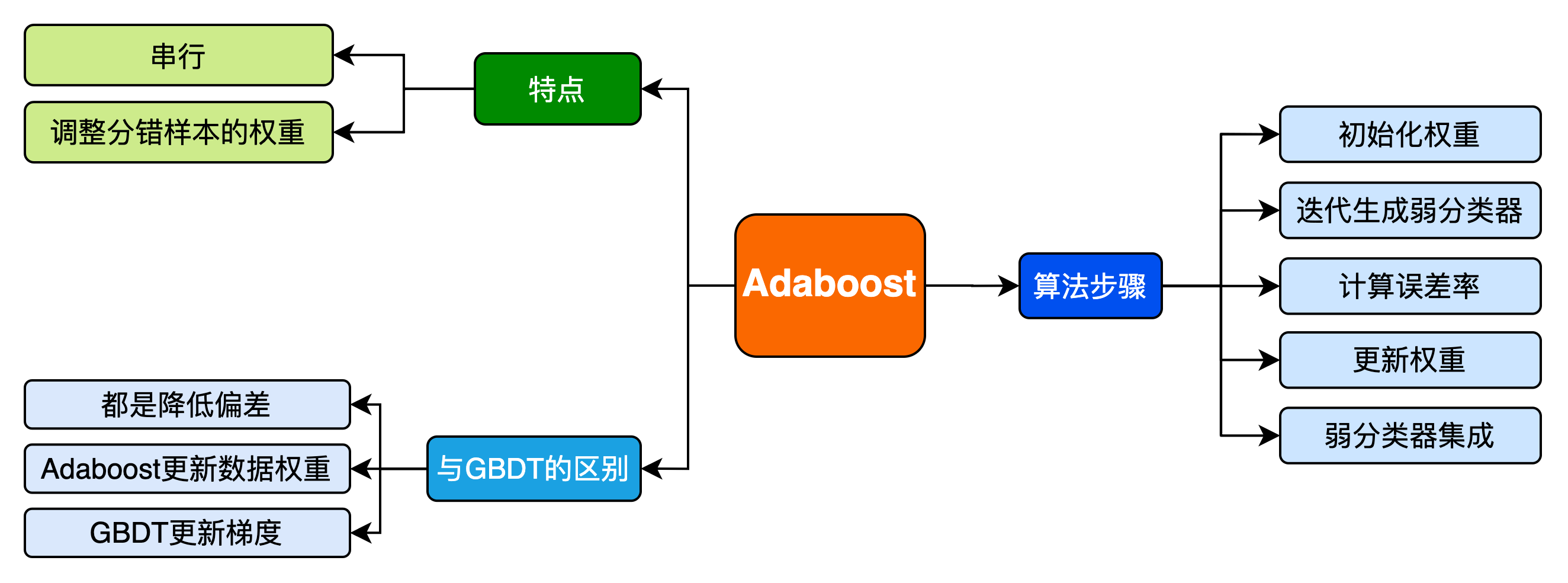
2.1 Adaboost 步骤概览

1. 初始化训练样本的权值分布，每个训练样本的权值应该相等（如果一共有$N$个样本，则每个样本的权值为$\frac{1}{N}$)

2. 依次构造训练集并训练弱分类器。如果一个样本被准确分类，那么它的权值在下一个训练集中就会降低；相反，如果它被分类错误，那么它在下个训练集中的权值就会提高。权值更新过后的训练集会用于训练下一个分类器。

3. 将训练好的弱分类器集成为一个强分类器，误差率小的弱分类器会在最终的强分类器里占据更大的权重，否则较小。

2.2 Adaboost 算法流程

给定一个样本数量为$m$的数据集

$$T=\{(x_1,y_1),\dots ,(x_m,y_m)\}$$

$y_i$ 属于标记集合$\{-1,+1\}$。

训练集的在第$k$个弱学习器的输出权重为

$$D(k)=(w_{k1},w_{k2},\dots w_{km});w_{1i}=\frac{1}{m};i=1,2\dots m$$

• 初始化训练样本的权值分布，每个训练样本的权值相同：

$$D(1)=(w_{11},w_{12},\dots w_{1m});w_{1i}=\frac{1}{m};i=1,2\dots m$$

• 进行多轮迭代，产生$T$个弱分类器。
  • 使用权值分布 $D(t) $的训练集进行训练，得到一个弱分类器

$$G_t(x):\chi \to \{-1,+1\}$$

• 计算 $G_t(x)$ 在训练数据集上的分类误差率（其实就是被 $G_t(x) $误分类样本的权值之和）:

$$e_t=P(G_t\left(x_i\right)\ne y_i)=\sum _{i=1}^m{w}_{ti}I(G_t\left(x_i\right)\ne y_i)$$

• 计算弱分类器 Gt(x) 在最终分类器中的系数(即所占权重)

$${\alpha }_t=\frac{1}{2}\ln \frac{1-e_t}{e_t}$$

• 更新训练数据集的权值分布，用于下一轮（t+1）迭代

$$D(t+1)=(w_{t+1,1},w_{t+1,2},\cdots w_{t+1,i}\cdots ,w_{t+1,m})$$$$w_{t+1,i}=\frac{w_{t,i}}{Z_t}\times \{\begin{array}{ll}{e}^{-{\alpha }_t}& \text{（}if{G}_t\left(x_i\right)=y_i）\\ e^{{\alpha }_t}& \text{（}if{G}_t\left(x_i\right)\ne y_i）\end{array}=\frac{w_{t,i}}{Z_t}\exp (-{\alpha }_t{y}_i{G}_t\left(x_i\right))$$

	其中 $Z_t$是规范化因子，使得$D(t+1)$成为一个概率分布（和为1）：

$$Z_t=\sum _{j=1}^m{w}_{t,i}\exp (-{\alpha }_t{y}_i{G}_t\left(x_i\right))$$

• 集成$T$个弱分类器为1个最终的强分类器：

$$G(x)=\mathrm{sign}(\sum _{t=1}^T{\alpha }_t{G}_t(x))$$

3. 算法面试题

3.1 Adaboost分类模型的学习器的权重系数$\alpha$怎么计算的？

Adaboost是前向分步加法算法的特例，分类问题的时候认为损失函数指数函数。

1. 当基函数是分类器时，Adaboost的最终分类器是：

   $$f(x)=\sum _{m-1}^M{\alpha }_m{G}_m(x)=f_{m-1}(x)+{\alpha }_m{G}_m(x)$$

2. 目标是使前向分步算法得到的$\alpha$和$G_m(x)$使$f_m(x)$在训练数据集T上的指数损失函数最小，即

   $$(\alpha ,G_m(x))=argmi{n}_{\alpha ,G}\sum _{i=1}^{N}exp[-y_i(f_{m-1}(x_i)+\alpha G(x_i))]$$

   其中，${\hat{w}}_{mi}=exp[-y_i{f}_{m-1}(x_i)].$为了求上式的最小化，首先计算$G_m^{\ast }(x)$,对于任意的$\alpha >0$,可以转化为下式：

   $$G_m^{\ast }=argmi{n}_G\sum _{i=1}^N{\hat{w}}_{mi}I(y_i\ne G(x_i))$$

   之后求${\alpha }_m^{\ast }$,将上述式子化简，得到

$$\sum _{i=1}^N{\hat{w}}_{mi}exp[-y_i\alpha G(x_i)]=\sum _{y_i=G_m(x_i)}{\hat{w}}_{mi}{e}^{-\alpha }+\sum _{y_i\ne G_m(x_i)}{\hat{w}}_{mi}{e}^{\alpha }=(e^{\alpha }-e^{-\alpha })\sum _{i=1}^N{\hat{w}}_{mi}I(y_i\ne G(x_i))+e^{-\alpha }\sum _{i=1}^N{\hat{w}}_{mi}$$

将已经求得的$G_m^{\ast }(x)$带入上式面，对$\alpha$求导并等于0，得到最优的$\alpha$.

$$a_m^{\ast }=\frac{1}{2}log\frac{1-e_m}{e_m}$$

其中$e_m$是分类误差率:

$$e_m=\frac{\sum _{i=1}^N{\hat{w}}_{mi}I(y_i\ne G_m(x_i))}{\sum _{i=1}^N{\hat{w}}_{mi}}=\sum _{i=1}^N{\hat{w}}_{mi}I(y_i\ne G_m(x_i))$$

3.2 Adaboost能否做回归问题？

Adaboost也能够应用到回归问题，相应的算法如下: 输入: $T=(x_i,y_1),(x_i,y_1),...,(x_N,y_N)$, 弱学习器迭代次数$M$。 输出：强分类器$f(x)$.

1. 初始化权重，

   $$D(1)=w_{11},w_{12},...,w_{1N};w_{1i}=\frac{1}{N};i=1,2,..,N$$

2. 根据$m=1,2,...,M$;

   • 学习得到$G_m(x)$

   • 计算训练集上最大误差

     $$E_m=max|y_i-G_m(x_i)|,i=1,2,..,N$$

   • 计算样本的相对平方误差:

     $$e_{mi}=\frac{(y_i-G_m(x_i){)}^2}{E_m^2}$$

   • 计算回归误差率:

     $$e_m=\sum _{i=1}^N{w}_{mi}{e}_{mi}$$

   • 计算学习器系数:

     $${\alpha }_m=\frac{e_m}{1-e_m}$$

   • 更新样本权重：

     $$w_{m+1,i}=\frac{w_{mi}}{Z_m}{\alpha }_m^{1-e^{m,i}}$$

     其中$Z_m$是规范化因子，

     $$Z_m=\sum _{i=1}^m{w}_{mi}{\alpha }_m^{1-e^{m,i}}$$

3. 得到强学习器：

   $$f(x)=\sum _{m=1}M{G}_m^{\ast }(x)$$

注: 不管是分类问题还是回归问题，根据误差改变权重就是Adaboost的本质，可以基于这个构建相应的强学习器。

3.3 boosting和bagging之间的区别,从偏差-方差的角度解释Adaboost？

集成学习提高学习精度，降低模型误差，模型的误差来自于方差和偏差，其中bagging方式是降低模型方差，一般选择多个相差较大的模型进行bagging。boosting是主要是通过降低模型的偏差来降低模型的误差。其中Adaboost每一轮通过误差来改变数据的分布，使偏差减小。

3.4 为什么Adaboost方式能够提高整体模型的学习精度？

根据前向分布加法模型，Adaboost算法每一次都会降低整体的误差，虽然单个模型误差会有波动，但是整体的误差却在降低，整体模型复杂度在提高。

3.5 Adaboost算法如何加入正则项?

$$f_m(x)=f_{m-1}(x)+\eta {\alpha }_m{G}_m(x)$$

3.6 Adaboost使用m个基学习器和加权平均使用m个学习器之间有什么不同？

Adaboost的m个基学习器是有顺序关系的，第k个基学习器根据前k-1个学习器得到的误差更新数据分布，再进行学习，每一次的数据分布都不同，是使用同一个学习器在不同的数据分布上进行学习。加权平均的m个学习器是可以并行处理的，在同一个数据分布上，学习得到m个不同的学习器进行加权。

3.7 Adaboost和GBDT之间的区别？

相同点：

Adaboost和GBDT都是通过减低偏差提高模型精度，都是前项分布加法模型的一种，

不同点:

Adaboost每一个根据前m-1个模型的误差更新当前数据集的权重，学习第m个学习器；

GBDT是根据前m-1个的学习剩下的label的偏差，修改当前数据的label进行学习第m个学习器，一般使用梯度的负方向替代偏差进行计算。

3.8 Adaboost的迭代次数(基学习器的个数)如何控制？

一般使用earlystopping进行控制迭代次数。

3.9 Adaboost算法中基学习器是否很重要，应该怎么选择基学习器？

sklearn中的adaboost接口给出的是使用决策树作为基分类器，一般认为决策树表现良好，其实可以根据数据的分布选择对应的分类器，比如选择简单的逻辑回归，或者对于回归问题选择线性回归。

3.10 MultiBoosting算法将Adaboost作为Bagging的基学习器，Iterative Bagging将Bagging作为Adaboost的基学习器。比较两者的优缺点？

两个模型都是降低方差和偏差。主要的不同的是顺序不同。MultiBosoting先减低模型的偏差再减低模型的方差，这样的方式 MultiBoosting由于集合了Bagging，Wagging，AdaBoost，可以有效的降低误差和方差，特别是误差。但是训练成本和预测成本都会显著增加。 Iterative Bagging相比Bagging会降低误差，但是方差上升。由于Bagging本身就是一种降低方差的算法，所以Iterative Bagging相当于Bagging与单分类器的折中。

3.11 训练过程中，每轮训练一直存在分类错误的问题，整个Adaboost却能快速收敛，为何？

每轮训练结束后，AdaBoost 会对样本的权重进行调整，调整的结果是越到后面被错误分类的样本权重会越高。而后面的分类器为了达到较低的带权分类误差，会把样本权重高的样本分类正确。这样造成的结果是，虽然每个弱分类器可能都有分错的样本，然而整个 AdaBoost 却能保证对每个样本进行正确分类，从而实现快速收敛。

3.12 Adaboost 的优缺点？

优点：能够基于泛化性能相当弱的的学习器构建出很强的集成，不容易发生过拟合。  

缺点：对异常样本比较敏感，异常样本在迭代过程中会获得较高的权值，影响最终学习器的性能表现。

参考资料：

1. 台湾清华大学李端兴教授2017年秋机器学习概论课程(CS 4602)PPT
2. 周志华 《机器学习》第8章 集成学习
3. July的博客
4. http://fornlp.com/周志华-《机器学习》-答案整理/