EasyVectorDB 教程

Step by step

首先，打开魔搭社区https://www.modelscope.cn/my/mynotebook 进入自己的主页，打开GPU环境的notebook。
然后打开终端，输入以下指令

shell

git clone  https://github.com/google-deepmind/limit.git

然后，因为代码中device参数的问题，你需要把我的代码复制过去，替换掉对应的文件。保存。
将本教程中free_embedding_experiment.py文件替换掉你clone下来的代码的free_embedding_experiment.py文件。
创建虚拟环境

shell

python3 -m venv venv
# 记得每次启动的时候都要进入虚拟环境！
source venv/bin/activate

下载下来后，你可以看到limit文件夹，然后你需要进入里面的code文件夹，然后在终端执行

shell

pip install -r requirements.txt

运行generate_li......文件，按照步骤一步一步来即可，生成所需要的数据集，关于数据集的含义，后面再讲解，先看到效果，再学习概念理论。
运行成功后，执行以下指令，运行测试

shell

python free_embedding_experiment.py --d=4 --k=2 --enable_critical_n_search=11 --results_output_path="result_d4_k2.json" --device="cpu"

或者使用GPU，但在使用GPU之前，如果你已经按照了JAX，请卸载（为什么呢？因为JAX为了轻量化，默认的 pip install jax 只安装CPU版本。您必须明确地安装为GPU编译的版本。）

如果你想要尝试d=15这种高维度的，一定要使用gpu，cpu的处理速度太慢了，不过，对于效果而言，尝试d=4，这种低维度的就够了。首先卸载当前的JAX然后重装GPU版本

shell

pip uninstall jax jaxlib
pip install -U "jax[cuda12_pip]" -f https://storage.googleapis.com/jax-releases/jax_cuda_releases.html
# 这个命令会非常慢，毕竟是国外的，但是等一会就好了，多重试几次

然后再执行下面的指令

shell

python free_embedding_experiment.py --d=4 --k=2 --enable_critical_n_search=11 --resultsg_output_path="result_d4_k2.json" --device="gpu"

如果报错了，看看是不是版本冲突，

shell


pip list | grep jax

正常情况下，你删除jax后执行这个指令是看不到任何jax的输出的，如果有，看一看是不是某个jax没有卸载好，重新把它卸载掉即可。

然后再执行安装Gpu版本的jax，此处CUDA为12_1版本。

然后再次执行

shell

pip list | grep jax

次，您应该能看到三个包都被列出来了，类似下面这样（版本号可能会有细微差别）：

shell

jax                      0.4.30
jax-cuda12-pjrt          0.6.2
jaxlib                   0.4.30

如果少了某个，执行python -c "import jax; print(jax.devices())" 看一看输出什么。不行就再重新安装。

为了更好的展现效果，你可以调整参数，将d调整为5、6 or other 然后输出文件路径改为result_d5_k2.json或者其他，这里我尝试d为4、5、6三种参数，生成了对应的三个json文件（在result目录下，如果你不想等待，可以直接使用，记得修改outplt文件中的地址为你生成的json文件路径）。
进入outplt.ipynb文件，依次执行，最终你将会看到效果图。

执行参数的含义

参数	说明	示例
--d	嵌入的维度	--d=8
--k	每个查询的相关文档数量	--k=2
--enable_critical_n_search	临界 N 搜索的起始值（初始文档数量）	--enable_critical_n_search=20
--results_output_path	实验结果保存的路径（JSON）	--results_output_path="results.json"
--device	训练使用的设备（gpu/cpu/tpu）	--device=gpu
--learning_rate	学习率	--learning_rate=0.01
--num_iterations	最大训练步数	--num_iterations=100000
--show_progress	是否显示进度条	--show_progress=True
--early_stopping_patience	早停耐心轮数	--early_stopping_patience=1000

预估时间消耗

shell

python free_embedding_experiment.py --d=15 --k=2 --enable_critical_n_search=11 --results_output_path="result_d15_k2.json" --device="cpu"

查看终端如下：

shell

I0908 16:19:06.376164 140021081243136 free_embedding_experiment.py:88] Optimizing (n=71,d=15,k=2):   2%|1         | 1701/100000 [19:07<17:57:08,  1.52it/s, loss=0.9497 acc=0.9990]

1. “一轮” vs “一步”

从开始优化 n=10 直到它完成，然后准备开始 n=11，这整个过程我们称之为“一轮”。

而现在看到的 1351/100000，是我们之前没有讨论到的、更细粒度的内部优化步骤。

2. 详细解读

Optimizing (n=71,d=15,k=2):

这告诉我们，脚本已经完成了 n=70 的优化，并且现在刚刚开始 n=71 这一轮。

1%| | 1351/100000 [15:18<18:00:06, 1.52it/s, loss=0.9506 acc=0.9994]

100000: 这是代码里设置的总优化**步骤(steps)**数量。为了让模型充分学习，作者设置了一个很大的数字（10万步）。
1351: 这是在 n=71 这一轮里，目前已经完成了 1351 步，1351变到1352算是一次计算，但这只是10万步中的一小步，我们称之为一个step或一个batch。
[15:18<18:00:06]:
- 15:18: 表示 n=71 这一轮已经进行了15分18秒。
- <18:00:06: 这是 tqdm 根据当前速度预估的剩余时间。它认为，光是跑完 n=71 这一轮，还需要18个小时
1.52it/s: 当前的优化速度，每秒能完成约1.5个小步骤（iterations/steps）。

数据集含义

这里详细解释一下 LIMIT 数据集的格式和用处。

这些数据是论文中"Free Embedding Optimization"实验的结果，它模拟了在不同维度 (d) 下，嵌入模型理论上能够捕获的文档组合数量。

d: 这是嵌入的维度。论文的核心观点是，嵌入的维度是限制模型表示文档组合能力的关键因素。
n: 这是文档的数量。在这些实验中，n 是指能够被模型成功表示的文档的最大数量，同时保持给定的维度 d 和 k (top-k 组合中的 k)。
k: 这是 "top-k" 组合中的 k 值。在这些实验中，k 固定为 2，意味着模型需要识别出两个相关的文档。
actual_q_generated: 这代表在给定 n 和 k 的情况下，所有可能的 top-k 相关文档组合的实际数量。例如，如果 n=5 且 k=2，则可能的组合数量为 $(\binom{5}{2}) = \frac{5 \times 4}{2 \times 1} = 10$ 。
final_accuracy 和 max_accuracy_observed: 这些指标表示模型在给定维度 d 下成功捕获所有相关文档组合的准确性。1.0 的准确率意味着模型能够完美地表示所有组合。
final_loss 和 best_loss_monitored: 这些是优化过程中的损失值。较低的损失值通常意味着更好的性能，因为模型能够更好地满足检索任务的约束。

了解完这些字段的含义后，如何通过数据得到论文的结论呢？

回顾一下论文的结论：嵌入模型的表示能力受到其维度的限制，并且存在一个"临界点"，在这个点之后，模型即使在理论最佳情况下也无法完全捕获所有可能的文档组合。

我们可以通过以下观察来印证这个结论：

维度 d 对准确率的影响：
- 不要忘记了，这里的n是能够被模型成功表示的文档的最大数量，d是嵌入向量的维度。
- 当 d=4 且 n=5 时，actual_q_generated 是 10，final_accuracy 是 1.0。这意味着在 d=4 的维度下，模型能够完美地表示这 10 种组合。
- 当 d=4 且 n=6 时，actual_q_generated 是 15，final_accuracy 仍然是 1.0。模型依然能够完美表示。
- 随着 n 的增加，actual_q_generated (即需要表示的组合数量) 也会迅速增加。
- 然而，当你查看 n=11, n=12, n=13, n=14 的结果时，会发现 final_accuracy 开始下降，并且不再是 1.0。例如，对于 d=4 和 n=11，final_accuracy 降到了 0.9090909090909091。这表明当文档数量 n 达到某个值时，即使维度 d 保持不变，模型也无法再完美地表示所有组合。
- 不过，d选择4、5、6这种极低的维度：这种情况下，实验结果更多地反映了维度过低导致的表示能力不足，而不是论文想要强调的即使在较高维度下，面对"所有组合"时的固有局限性。
- 我的建议是，为了更好地体现论文在实际情况下的限制，你应该至少从 d=32 开始，并尝试一些更高的维度。（我只是建议，你可不要真的尝试这些维度，太慢了。）
  最低起点：d=32
  这是论文中 SOTA 模型评估的最低维度（参见 Figure 3 和 Figure 4）。从这个点开始，你可以直接与论文中的 SOTA 模型在低维度下的表现进行比较。常见和有代表性的维度：d=128, 256, 512, 768, 1024
  这些维度更接近真实世界中嵌入模型常用的维度，尤其是在各种预训练模型中。 d=768 和 d=1024 尤其重要，因为它们是许多主流语言模型（如 BERT base/large, RoBERTa 等）的默认输出维度。论文也明确指出 1024 维对应 400 万文档的 Critical-n，这在一定程度上是实际应用中的一个限制。
  这些是论文中评估的最高维度，能够显示在更大规模文档集下（如几百万到几亿），即便是非常大的维度也无法满足所有组合的需求。如果你的实验资源有限，可以优先考虑上述"常见和有代表性"的维度，我这里就只尝试了4、5、6了。
"临界点"的体现：
- 对于每个固定的维度 d，会有一个 n 的最大值，模型能够以 100% 的准确率表示所有组合。一旦 n 超过这个"临界值"，准确率就会下降。
- 表格 6 (Table 6) 中列出了 d 和对应的 Critical-n 值，这直接展示了在不同的嵌入维度 d 下，模型能够成功表示所有 top-k 组合的最大文档数量 n。例如，当 d=4 时，Critical-n 是 10。这与你在 n=11 观察到的准确率下降相吻合。
损失值的变化：
- 随着 n 超过 Critical-n，即使损失值可能会持续下降，但准确率却无法达到 1.0。这进一步支持了即使在最佳优化情况下，模型也无法完美捕获所有组合的观点。

简而言之，这些数据实证地验证了，对于给定的嵌入维度 d 和 k，存在一个文档数量 n 的上限，超过这个上限，即使是经过最佳优化的嵌入模型也无法完美地表示所有可能的 top-k 文档组合。这就是论文所指出的嵌入模型在表示能力上的理论局限性。

1. 数据集格式

主要包含哪些内容？

从 Notebook 的结构来看，LIMIT 数据集主要由以下几部分组成：

1 用户数据

名字和姓氏：从公开源下载大量的英文名字和姓氏，组合成唯一用户，例如：Alice Smith, Bob Johnson。
唯一性：去重后有约2700多个名字，1000多个姓氏。可以组成上百万个独立用户。

2 物品数据

items_to_like：这是一个超长的物品列表，包括：
- 食物（水果、蔬菜、肉类、饮料）
- 动物（宠物、野生动物、昆虫等）
- 植物（花、树、草药等）
- 自然现象（雨、雪、云、月亮等）
- 运动与活动（足球、游泳、徒步等）
- 其他类别（蛋糕、糖果、面包、调味料等）

3 用户偏好

格式举例：
- 每个用户可以"喜欢"若干物品，通常以表格或 JSON 的形式存储：
  - CSV:
    user_name item
    Alice Smith Apple
    Bob Johnson Soccer
  - JSON:
    json
```
[
  {"user": "Alice Smith", "likes": ["Apple", "Soccer", "Rain"]},
  {"user": "Bob Johnson", "likes": ["Banana", "Basketball"]}
]
```
    1
    2
    3
    4
生成方式：可以随机分配每个用户喜欢的物品数量（如每人5-10个），根据实际需要生成交互数据。

user_name	item
Alice Smith	Apple
Bob Johnson	Soccer

结果文件的含义

"final_accuracy"：每个 N 的最终准确率
"final_loss"：优化终点的 loss
"max_accuracy_observed"：整个 10w 次迭代中的最大准确率
"actual_q_generated"：实际采样到的 query/相关文档配置总数
"optimization_duration_seconds"：优化过程所用时间
"accuracies"/"losses"：每隔一段迭代记录的准确率/loss 曲线，可用于画图分析模型收敛过程

我们从d=3的结果文件来看，这些数据是论文中"Free Embedding Optimization"实验的结果，它模拟了在不同维度 (d) 下，嵌入模型理论上能够捕获的文档组合数量。这些数据对于理解论文的核心结论至关重要。

让我来解释一下这些数据的含义，以及它们如何支持论文的结论：

d: 这是嵌入的维度。论文的核心观点是，嵌入的维度是限制模型表示文档组合能力的关键因素。
n: 这是文档的数量。在这些实验中，n 是指能够被模型成功表示的文档的最大数量，同时保持给定的维度 d 和 k (top-k 组合中的 k)。
k: 这是 "top-k" 组合中的 k 值。在这些实验中，k 固定为 2，意味着模型需要识别出两个相关的文档。

actual_q_generated: 这代表在给定 n 和 k 的情况下，所有可能的 top-k 相关文档组合的实际数量。例如，如果 n=5 且 k=2，则可能的组合数量为 $(\binom{5}{2}) = \frac{5 \times 4}{2 \times 1} = 10$ 。

final_accuracy 和 max_accuracy_observed: 这些指标表示模型在给定维度 d 下成功捕获所有相关文档组合的准确性。1.0 的准确率意味着模型能够完美地表示所有组合。

final_loss 和 best_loss_monitored: 这些是优化过程中的损失值。较低的损失值通常意味着更好的性能，因为模型能够更好地满足检索任务的约束。

如何通过数据得到论文的结论：

论文的结论是，嵌入模型的表示能力受到其维度的限制，并且存在一个"临界点"（critical-n），在这个点之后，模型即使在理论最佳情况下也无法完全捕获所有可能的文档组合。你可以通过以下观察来印证这个结论：

维度 d 对准确率的影响：

当 d=4 且 n=5 时，actual_q_generated 是 10，final_accuracy 是 1.0。这意味着在 d=4 的维度下，模型能够完美地表示这 10 种组合。
当 d=4 且 n=6 时，actual_q_generated 是 15，final_accuracy 仍然是 1.0。模型依然能够完美表示。

随着 n 的增加，actual_q_generated (即需要表示的组合数量) 也会迅速增加。

然而，当你查看 n=11, n=12, n=13, n=14 的结果时，会发现 final_accuracy 开始下降，并且不再是 1.0。例如，对于 d=4 和 n=11，final_accuracy 降到了 0.9090909090909091。这表明当文档数量 n 达到某个值时，即使维度 d 保持不变，模型也无法再完美地表示所有组合。

"临界点"的体现：

对于每个固定的维度 d，会有一个 n 的最大值，模型能够以 100% 的准确率表示所有组合。一旦 n 超过这个"临界值"，准确率就会下降。

表格 6 (Table 6) 中列出了 d 和对应的 Critical-n 值，这直接展示了在不同的嵌入维度 d 下，模型能够成功表示所有 top-k 组合的最大文档数量 n。例如，当 d=4 时，Critical-n 是 10。这与你在 n=11 观察到的准确率下降相吻合。

损失值的变化：

随着 n 超过 Critical-n，即使损失值可能会持续下降，但准确率却无法达到 1.0。这进一步支持了即使在最佳优化情况下，模型也无法完美捕获所有组合的观点。

简而言之，这些数据实证地验证了，对于给定的嵌入维度 d 和 k，存在一个文档数量 n 的上限，超过这个上限，即使是经过最佳优化的嵌入模型也无法完美地表示所有可能的 top-k 文档组合。这就是论文所指出的嵌入模型在表示能力上的理论局限性。

结果图片的含义

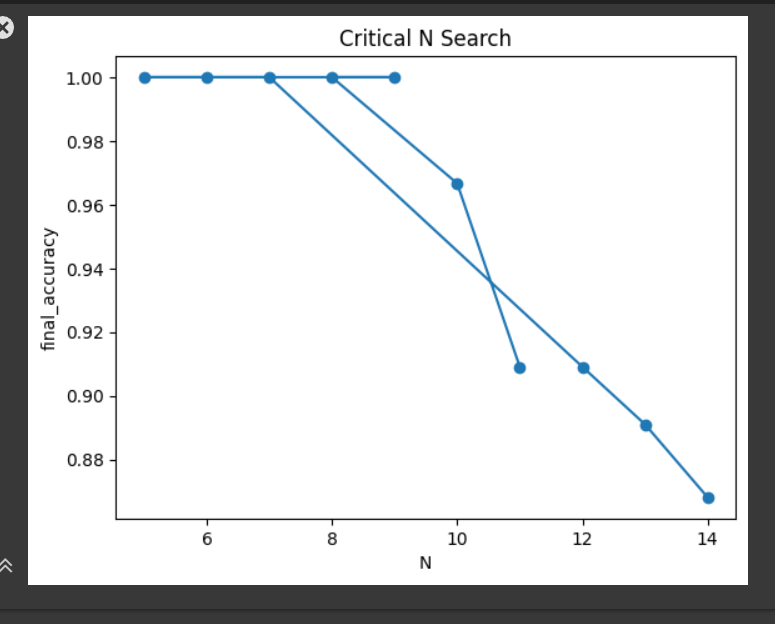
这张图表展示了在特定嵌入维度 d 和 k（在这个实验中 d=4, k=2）下，随着文档数量 N 的增加，最终准确率 (final_accuracy) 的变化。

X 轴 (N)：这代表了文档的数量。在这些实验中，N 的值从 5 开始逐渐增加。

Y 轴 (final_accuracy)：这表示模型在给定 N 值下，能够正确捕获所有 top-k 相关文档组合的准确率。1.00 表示 100% 的准确率，意味着模型完美地完成了任务。

这张图直观地展示了论文中关于嵌入模型表示能力局限性的核心观点：嵌入模型的表示能力是有限的，并且当需要处理的文档组合数量超过某个临界值时，即使是简单任务，模型也无法完美完成。

初始阶段的高准确率：你可以看到，当 N 较小（例如 N=5, N=6, N=7）时，final_accuracy 保持在 1.00，这意味着模型能够完美地表示所有组合。这与我们之前看到的数据结果一致，表明在文档数量不多时，模型可以很好地工作。

"临界点"的出现：当 N 增加到 8 之后，图表上出现了一个转折点。虽然在 N=8 时准确率仍然是 1.00，但随后在 N 进一步增加时，final_accuracy 开始显著下降（例如，N=10 时大约是 0.96，N=11 时大约是 0.91）。这个下降趋势表明，随着需要表示的文档组合数量的增加，即使是经过优化的嵌入模型也无法再保持 100% 的准确率。

表示能力的局限性：准确率的下降清楚地表明，对于给定的嵌入维度（这里是 d=4），存在一个文档数量的"临界值"（Critical-n）。一旦文档数量超过这个值，模型就无法完全捕获所有可能的文档组合。这张图形象地展示了表格 6 中 d=4 对应的 Critical-n 值（即 10）以及之后准确率的下降。

现在我们综合一下，当d=4\5\6的时候，结果图以及其为我们所展示的含义

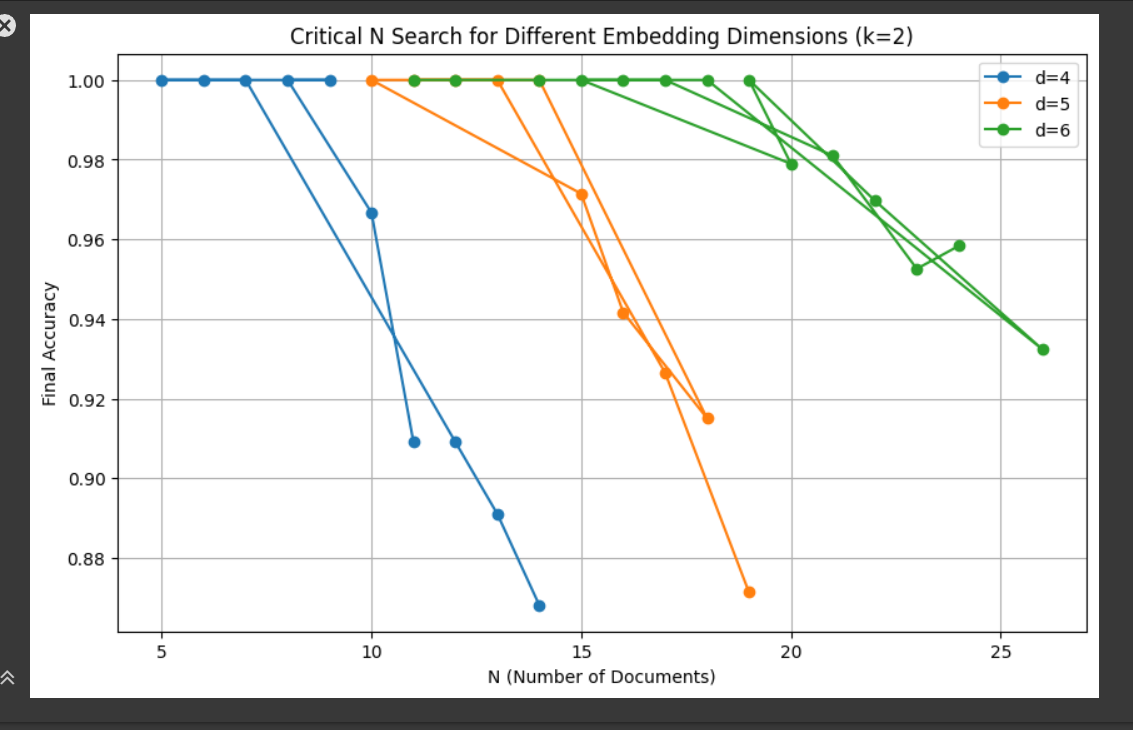
这张图表通过三条不同颜色的线，描绘了在 k=2 的情况下，不同嵌入维度 (d=4, d=5, d=6) 如何影响模型识别所有可能文档组合的准确率。 从图中我们可以看到：

维度 d 对"临界点"的影响：
- 对于 d=4 (蓝色线)，准确率在文档数量 N=10 时开始从 1.00 下降。这意味着当维度为 4 时，模型能够完美表示的最大文档数量（Critical-n）是 10。
- 对于 d=5 (橙色线)，准确率在文档数量 N=14 时开始从 1.00 下降。这意味着当维度为 5 时，Critical-n 是 14。
- 对于 d=6 (绿色线)，准确率在文档数量 N=19 时开始从 1.00 下降。这意味着当维度为 6 时，Critical-n 是 19。
- ...
- 这明确表明，嵌入维度越高，模型能够完美表示所有可能组合的文档数量就越多。
论文结论的直观展示：
- 这张图直接展示了论文的核心观点：嵌入模型的表示能力受到其维度的根本性限制。
- 对于每个固定的维度，都存在一个文档数量的上限（即 Critical-n），超过这个上限，即使是理想的嵌入模型也无法完美地表示所有可能的文档组合。更高的维度确实允许模型处理更多的文档，但这种局限性仍然存在。

这张图表的数据与论文中的 Table 6 是吻合的。Table 6 列出的 Critical-n 值就是图中准确率首次从 1.00 下降时的 N 值。

Table 6 显示 d=4 对应 Critical-n=10。
d=5 对应 Critical-n=14。
d=6 对应 Critical-n=19。

如果你尝试 128 或 1024 维度的临界值，正如我们之前讨论的，理论上它们能够表示的文档数量会更多（如 Table 6 中的外推值）。然而，计算这些高维度的 Critical-n 会变得非常复杂和耗时，因为可能的文档组合数量会呈指数级增长，论文中也提到了计算的难度，所以，试一试低维的就可以，剩下的时间去吃个大盘鸡(　o=^•ェ•)o🍚。

Step by step ​

执行参数的含义 ​

预估时间消耗 ​

1. “一轮” vs “一步” ​

2. 详细解读 ​

数据集含义 ​

1. 数据集格式 ​

主要包含哪些内容？ ​

1 用户数据 ​

2 物品数据 ​

3 用户偏好 ​

结果文件的含义 ​

如何通过数据得到论文的结论： ​

"临界点"的体现： ​

损失值的变化： ​

结果图片的含义 ​

Step by step

执行参数的含义

预估时间消耗

1. “一轮” vs “一步”

2. 详细解读

数据集含义

1. 数据集格式

主要包含哪些内容？

1 用户数据

2 物品数据

3 用户偏好

结果文件的含义

如何通过数据得到论文的结论：

"临界点"的体现：

损失值的变化：

结果图片的含义