将向量压缩发挥到极致：Milvus 如何利用 RaBitQ 将查询次数提高 3 倍

这里引用了Milvus官方博客的标题，原文链接请点击-->博客原文

RabitQ现以集成到Milvus 2.6.x版本中，这种新技术使得Milvus可以以更低的内存成本提供三倍以上的流量，同时只牺牲了极少的准确率。

RabitQ介绍

RaBitQ（全称 Randomized Bit Quantization）是一种用于高维向量近似最近邻搜索（Approximate Nearest Neighbor Search, ANNS）的新型量化方法，由南洋理工大学等机构的研究者在 SIGMOD 2024 上提出。它的核心目标是在极大地压缩向量存储空间（如将每个维度压缩至 1 bit）的同时，通过数学方法保证距离估算的准确性，并提供严谨的理论误差界限。 RaBitQ 的出现主要解决了传统量化方法（如乘积量化 PQ）在大规模向量数据库中计算开销大或缺乏理论保证的问题。它通过随机旋转和投影技术，将原始的高维欧几里得空间映射到离散的比特串空间，使得原本复杂的浮点数距离计算可以转化为极快的位运算（bitwise operations）。目前，该技术已被 LanceDB 和 Elasticsearch 等主流向量数据库关注或集成，用于提升检索速度。

传统搜索算法所面临的挑战

在深入了解RabitQ之前，我们先了解一下传统方法所面临的挑战

ANN近似搜索算法是向量数据库的核心，它能够找到给定的查询的最相近的TopK个向量，但随着向量规模的扩大，存储和计算需求也随之增加，尤其是使用FLAT和HNSW算法的情况下，计算和存储成本将随着数据规模成倍增加，可以使用->Milvus资源计算工具来查看具体资源消耗。

现有的标量量化（SQ）和乘积量化（PQ）是目前流行的压缩技术，都是通过向量的分块压缩计算，使得可以用更少的比特表示相同的信息，大大减少了内存使用量，但代价是，召回率随着压缩倍率而明显下降。

这些挑战，促使了RabitQ算法脱颖而出，这种出色的压缩技术使得在保持高召回率的同时大幅度压缩向量。该方法实现了具有O(1/√D)误差界限的无偏距离估计器，并在多个数据集上超越了最先进的方法。

Milvus中的RabitQ工程

RabitQ要求每个向量有两个浮点值需要在索引构建时预先计算，第三个值是可以动态配置计算或者预先计算的，Milvus在其核心向量搜索引擎中预先计算了这个值，并将其存储起来，以提高检索效率。

从Milvus2.6版本后，Milvus引入了IVF_RABITQ索引类型，这种索引将RabitQ和IVF聚类、随机旋转变化和可选细化相结合，在性能、内存效率和准确性之间实现了最佳平衡。

可以使用如下的方式构建：

python

from pymilvus import MilvusClient
index_params = MilvusClient.prepare_index_params()

index_params.add_index(
    field_name = "你的向量字段",
    index_type = "IVF_RABITQ"，
    index_name = "向量索引",
    metric_type = "IP",
    params = {
        "nlist":1024,
    }
)

其中params可以选择以下参数：

nlist 和 nprobe 是所有基于 IVF 方法的标准参数。
nlist 是一个非负整数，用于指定数据集的 IVF 桶总数。
nprobe 是一个非负整数，用于指定搜索过程中单个数据向量所访问的 IVF 桶的数量。这是一个与搜索相关的参数。
rbq_bits_query 指定查询向量的量化程度。使用 1...8 值表示量化级别。使用 0 值可禁用量化。这是一个与搜索相关的参数。可用选项为 SQ1 到 SQ8。
refine, refine_type 和 refine_k 参数是细化过程的标准参数。
refine 是一个布尔值，用于启用细化策略。
refine_k 是一个非负的 fp 值。细化过程使用更高质量的量化方法，从 refine_k 倍的候选池中挑选出所需的近邻数量，这些候选池是通过 IVFRaBitQ 选取的。这是一个与搜索相关的参数。
refine_type 是一个字符串，用于指定细化索引的量化类型。可用选项为 FP16, BF16, FP32, FLAT, , 和 /。推荐选项为 SQ6 和 SQ8。

基准测试

该部分引用Milvus官方博客我们使用 vdb-bench 对不同的配置进行了基准测试，这是一款用于评估向量数据库的开源基准测试工具。测试和控制环境都使用了部署在 AWS EC2m6id.2xlarge 实例上的 Milvus Standalone。这些机器具有 8 个 vCPU、32 GB 内存和基于冰湖架构的英特尔至强 8375C CPU，该 CPU 支持 VPOPCNTDQ AVX-512 指令集。

我们使用 vdb-bench 中的搜索性能测试，数据集包含 100 万个向量，每个向量有 768 个维度。由于 Milvus 的默认分段大小为 1 GB，而原始数据集（768 维×100 万向量×每个浮点 4 字节）总计约为 3 GB，因此基准测试涉及每个数据库的多个分段。

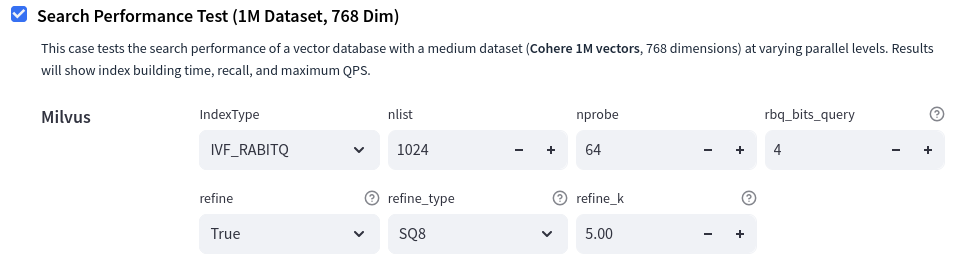
图vdb-bench 中的测试配置示例。

下面是 IVF、RaBitQ 和细化过程配置旋钮的一些低级细节：

nlist 和是所有基于方法的标准参数nprobe IVF
nlist 是一个非负整数，用于指定数据集的 IVF 桶总数。
nprobe 是一个非负整数，用于指定搜索过程中单个数据向量所访问的 IVF 桶的数量。这是一个与搜索相关的参数。
rbq_bits_query 指定查询向量的量化程度。使用 1...8 值表示 ... 量化级别。使用 0 值可禁用量化。这是一个与搜索相关的参数。SQ1SQ8
refine,refine_type 和refine_k 参数是细化过程的标准参数
refine 是一个布尔值，用于启用细化策略。
refine_k 是一个非负的 fp 值。细化过程使用更高质量的量化方法，从倍的候选池中挑选出所需的近邻数量，这些候选池是通过选取的。这是一个与搜索相关的参数。refine_k IVFRaBitQ
refine_type 是一个字符串，用于指定细化索引的量化类型。可用选项为 , , , 和 / 。SQ6 SQ8 FP16 BF16 FP32 FLAT

结果揭示了重要的启示：

图：采用不同细化策略的基准 (IVF_FLAT)、IVF_SQ8 和 IVF_RABITQ 的成本和性能比较

基线IVF_FLAT 索引的吞吐量为 236 QPS，召回率为 95.2%，相比之下，IVF_RABITQ 的吞吐量明显更高--使用 FP32 查询时为 648 QPS，使用 SQ8 量化查询时为 898 QPS。这些数据证明了 RaBitQ 的性能优势，尤其是在应用细化时。

不过，这种性能在召回率方面有明显的折损。在不进行细化的情况下使用IVF_RABITQ 时，召回率约为 76%，这对于要求高准确度的应用来说可能是不够的。尽管如此，使用 1 位向量压缩达到这样的召回率水平仍然令人印象深刻。

细化对恢复准确性至关重要。当配置 SQ8 查询和 SQ8 精炼功能时，IVF_RABITQ 可提供出色的性能和召回率。它保持了 94.7% 的高召回率，几乎与 IVF_FLAT 相当，同时达到了 864 QPS，比 IVF_FLAT 高出 3 倍多。即使与另一种流行的量化指数IVF_SQ8 相比，经过 SQ8 精炼的IVF_RABITQ 也能在相似的召回率下实现一半以上的吞吐量，只是成本略高。因此，对于既要求速度又要求准确性的应用场景来说，它是一个极佳的选择。

简而言之，IVF_RABITQ 本身就能在召回率可接受的情况下实现吞吐量最大化，如果再搭配细化功能，则功能更加强大，与IVF_FLAT 相比，只需占用一小部分内存空间，就能缩小质量差距。

RabitQ底层详解

总体设计

想象一下，你的任务是设计一个“通用尺子”，用它来近似测量地球（一个高维球面）上任何一个城市（一个数据向量）的位置。你只能在这把尺子上标记有限个刻度（码本向量）。

PQ的做法是这样的：

先收集地球上所有主要城市的位置数据。
通过聚类分析（K-Means），找到这些城市分布最密集的几个区域（比如东亚、西欧、北美）。
把这些区域的中心点作为尺子上的“刻度”。

这种“定制化”的尺子，在测量那些我们已经知道的城市群时会非常准。但它的缺点是：

带有偏见：它对数据密集的区域“过度优化”了。如果突然要测量一个在西伯利亚或者撒哈拉沙漠中心的新城市，这把尺子上可能根本没有一个合适的刻度，导致测量误差巨大。
无法预测：你无法从理论上保证这把尺子的最差表现有多差。它的性能完全依赖于你的数据分布，换一套数据，尺子就得重做，性能也可能天差地别。

RaBitQ 的思路：一把“公平”的尺子

RaBitQ认为，我们不应该去“迎合”现有的数据，而应该设计一把在数学上绝对公平、无偏见的尺子。

它的做法分为两步：

第一步：制造一个“完美的”刻度网格 (确定性码本 C)

先不考虑城市在哪，我们在地球上画一个“完美”的经纬网。这个网格非常规整、对称，覆盖全球。
在论文里，这个“完美的网格”就是由 ±1/√D 构成的超立方体顶点。它几何上非常漂亮，但它的朝向是固定的（比如0度经线、赤道都是定死的）。

第二步：给这个网格一个随机的“初始角度” (随机旋转 P)

这是最关键的一步！如果我们就用这个固定朝向的网格，万一所有城市恰好都在网格线的“缝隙”里，测量效果就会很差。
所以，RaBitQ在把这个“完美的网格”套上地球之前，先把它随机地旋转一下。就像你把一个地球仪模型拿在手里，先闭着眼睛随意转动它，然后再用它来测量。
在论文里，这个“随机旋转”就是通过乘以一个随机正交矩阵 P 来实现的。

为什么这个“随机旋转”如此重要？

消除了偏见：因为初始角度是随机的，所以对于地球上任何一个城市，它都不会系统性地处在一个“好测”或者“难测”的位置。这个尺子对全球任何一个点都是一视同仁的，是公平的。
带来了理论保证：正是因为这种随机性和公平性，我们才可以使用概率论和统计学工具来严格分析这把尺子的性能。我们可以从数学上证明：
- 用它进行多次测量，平均误差会趋向于零（无偏估计）。
- 单次测量的误差大小有一个明确的上限，而且这个误差会随着维度 D 的增加而减小（理论误差界）。
实现了鲁棒性：这把尺子的性能不再依赖于数据本身，所以它非常稳定和鲁棒。无论你要测量的是人口稠密的纽约，还是人迹罕至的南极科考站，它的性能表现都是可以预测的，不会出现“灾难性的失败”。

总结一下：

PQ试图通过学习数据来找到“最优”的码本，但这种最优是脆弱的、不可靠的。而RaBitQ放弃了这种对数据的“最优拟合”，转而追求一种基于随机化的“普遍公平性”，从而换来了强大的理论保证和实践中的稳定性。这就是它能够超越传统方法的根本原因。

生动的例子

我们可以把整个过程想象成建立一个高科技图书馆。

阶段一：索引阶段 (存储数据) - 整理所有图书并制作索引卡

这个阶段在你发起任何搜索之前，只需要做一次。目标是处理完你所有的数据（比如一百万张图片），为未来的快速搜索做好准备。

目标： 为图书馆里的每一本“书”（数据向量）制作一张高效的“索引卡”。

流程：

第一步：制造一个“魔法罗盘” (生成随机矩阵 P)
- 我们首先创建一个D x D维的随机正交矩阵P。这个矩阵是整个系统的核心，可以把它想象成一个校准过的、但初始方向完全随机的罗盘。
- 关键： 这个“罗盘”只制造一次，之后所有的操作都用这同一个罗盘。它被永久保存下来。
第二步：为每一本书（数据向量 o）制作索引卡
- 我们一本一本地处理图书馆里所有的书。对于每一本书（每一个数据向量o）：
  - A. 标准化处理： 先对向量o进行归一化，让它变成单位向量。这就像把所有书都统一成标准A4大小，方便处理。
  - B. 使用罗盘定位： 用“罗盘”的反向功能（P⁻¹）去“照射”这个向量，得到一个转换后的向量 o' = P⁻¹o。
  - C. 提取“二进制指纹” (生成量化码)： 查看 o' 的每一个维度。
    - 如果第 i 维是正数，记录为 1。
    - 如果第 i 维是负数，记录为 0。
    - 这样，我们就得到了一个D位的二进制字符串（比如 10110...）。这就是这本书独一无二的、压缩后的“指纹”。
  - D. 预计算“校准因子” (存储 ⟨ō, o⟩)：
    - 我们用刚刚生成的“指纹”和“罗盘P”，可以反向构造出近似向量ō。
    - 然后，我们计算**原始向量o和近似向量ō**之间的相似度 ⟨ō, o⟩。这是一个浮点数（比如0.813）。
    - 这个数值就是“校准因子”，它告诉我们量化过程造成了多大的“磨损”。
第三步：存储索引卡
- 现在，对于原始的每一本书o，我们都制作了一张索引卡。这张卡上存了三样东西：
  1. D位二进制指纹 (用于快速初筛)
  2. 浮点数“校准因子” (用于精确估算)
  3. 指向原始书本存放位置的ID (用于最后核对)
- 我们把所有这些“索引卡”存放在一个巨大的、易于访问的索引文件里。

阶段二：查询阶段 (查找数据) - 当一个读者来查书时

这个阶段在你输入一个查询向量（比如一张你想以图搜图的图片）时触发。

目标： 快速、准确地找到与“查询图书”（查询向量q）最相似的K本书。

流程：

第一步：处理读者的查询需求 (预处理查询向量 q)
- A. 标准化： 同样地，先把查询向量q归一化。
- B. 使用同一个罗盘定位： 用索引阶段保存的那个“魔法罗盘”，同样计算出 q' = P⁻¹q。
- C. 优化（可选）： 为了计算更快，可以把浮点向量q'压缩成4位整数向量。
第二步：快速浏览所有索引卡，进行初筛
- 我们遍历索引文件里的每一张“索引卡”。对于第i张卡：
  - A. 读取信息： 从卡上拿出“D位指纹”和“校准因子”。
  - B. 快速估算相似度 (计算分子)： 用查询向量q'和卡上的“D位指纹”进行一次极速的计算（这是通过位运算实现的），得到一个原始的相似度分数 ⟨ō, q⟩。
  - C. 校准估算结果 (套用公式)： 用上一步得到的分数，除以卡上存储的“校准因子”。 最终估算相似度 = 原始分数 / 校准因子
  - D. 转换成估算距离： 把这个校准后的相似度转换成估算的距离。
第三步：确定一个“候选书单”
- 在快速浏览完所有索引卡后，我们根据“估算距离”进行排序，选出距离最近的比如1000本书，形成一个“候选书单”。
第四步：精确核对候选书单 (重排 Re-ranking)
- 现在，我们不再看索引卡了。我们拿着这个只有1000本书的“候选书单”，去书库里把这1000本书的“原件”（原始的全精度向量）取出来。
- 我们用查询向量q和这1000个原始向量，逐一计算精确的、毫无水分的欧氏距离。
- 最后，根据这个精确距离排序，返回给读者最终的前10名结果。

技术细节

第一步：一个“完美”的基础码本 C

首先，我们忘掉随机，先看看基础码本 C 是什么。

它是什么？ 它是一个由 2^D 个向量组成的集合。D 是你原始数据的维度。
向量长什么样？ 每个向量的每一个坐标值要么是 +1/√D，要么是 -1/√D。
几何上代表什么？
- 想象一个二维空间 (D=2)。这些向量就是 (1/√2, 1/√2), (1/√2, -1/√2), (-1/√2, 1/√2), (-1/√2, -1/√2)。它们正好是一个单位圆（半径为1的圆）内接正方形的四个顶点。
- 想象一个三维空间 (D=3)。这些向量就是单位球体内接立方体的八个顶点。
- 在高维空间 (D维)，这些向量就是单位超球面内接超立方体的所有顶点。

这个码本 C 非常规整、对称，像一个“完美”的网格。但论文指出，这种过于规整的网格是有偏见的。如果你的数据向量正好跟坐标轴对得特别齐，它可能效果很好；但如果数据分布在一些“奇怪”的角度，这个固定的网格可能就无法很好地近似它们。

公式 C_rand = {Px | x ∈ C} 的本质，就是通过一次数据无关的随机旋转，将一个固定的、有潜在偏见的测量工具，变成了一个概率上公平、性能可预测的测量工具。

第二步：一次“公平”的随机旋转 P

为了打破第一步中那个“完美”网格的偏见，RaBitQ引入了最关键的一步：随机旋转。

P是什么？ P 是一个随机正交矩阵。在几何上，一个正交矩阵代表着旋转和反射，它最重要的特性是保范性和保角性，也就是说，它不会拉伸、压缩或扭曲空间。任何两个点经过它变换后，它们之间的距离和夹角都保持不变。
Px 是什么操作？ 就是将基础码本 C 里的每一个顶点向量 x 都进行一次由 P 定义的随机旋转，得到一个新的向量。
C_rand = {Px | x ∈ C} 是什么？ 就是把整个“完美”的超立方体网格，在超球面上随机地“滚一下”，让它停在一个随机的朝向上。

你可以想象一下，你手里有一个水晶做的、非常规整的立方体。如果你总是正着放它，那它的顶点永远指向固定的方向。但如果你把它抛向空中，让它随机落下，那它的顶点就会朝向各种随机的方向。这个“抛”的动作，就是 P 的作用。

第三步：牵连的知识及其作用

现在我们来回答最重要的部分：为什么要这么做？这对RaBitQ和实践有什么作用？

1. 相关知识：约翰逊-林登施特劳斯引理 (Johnson-Lindenstrauss Lemma, JLT)

这是背后最核心的理论。JLT简单来说就是：当你把高维空间中的点通过一个随机矩阵投影到一个更低维度的空间时，点与点之间的距离能够被以很高的概率近似地保留下来。

RaBitQ这里的随机旋转 P 正是JLT中随机矩阵的一种（正交随机矩阵）。虽然RaBitQ没有降低维度，但它利用了JLT的核心思想：随机性可以带来可预测的、公平的距离保持特性。

2. 对RaBitQ的理论作用：获得“理论误差保证”

这正是RaBitQ与PQ等方法的根本区别。

PQ的问题：PQ使用K-Means聚类来生成码本。K-Means是一个依赖于数据的启发式算法，你很难从理论上证明它的误差是多少。它的效果好坏完全取决于数据分布和算法的运气，因此论文说它“没有理论误差保证”，并且在某些数据集上会“灾难性地失败”。
RaBitQ的优势：由于RaBitQ的码本是通过数据无关的随机旋转生成的，整个量化过程变得可以在数学上进行严格分析。随机性确保了对于任何输入向量，这个码本都不会有系统性的偏见。这使得作者能够推导出清晰的公式，证明其距离估计是无偏的（平均而言是准确的），并且误差有一个明确的概率上界（误差大小为 O(1/√D)）。

简单说，随机性牺牲了对特定数据的“最优拟合”，换来了对所有数据的“公平性和可预测性”。

3. 在实践上的作用

理论上的优势会直接转化为实践中的好处：

稳定性和鲁棒性：因为有理论保证，RaBitQ的性能非常稳定。它不会像PQ那样，在一个数据集上表现优异，在另一个上就彻底崩溃。你知道它的最差表现也不会差到哪里去，这对于构建可靠的系统至关重要。
无需调参和训练：PQ的码本生成（K-Means）过程可能非常耗时。而RaBitQ的码本生成非常简单：只需要生成一个随机矩阵 P 即可，这个过程与数据无关，速度很快。
性能更优：如论文中的实验（图3和图4）所示，在大多数情况下，RaBitQ在相同的性能开销下，其距离估计的精度（平均相对误差和最大相对误差）都显著优于PQ。尤其是在PQ表现不佳的MSong数据集上，RaBitQ依然稳健。

总结

特性	RaBitQ 的码本构建 (随机化)	PQ 的码本构建 (启发式学习)
方法	旋转一个固定的、对称的网格 (`C_rand = Px`)	对数据进行K-Means聚类，取聚类中心
数据依赖性	数据无关	数据相关
理论保证	有，可以证明距离估计无偏，误差有界	无，是启发式的，性能无法预测
实践效果	稳定、鲁棒，在各种数据集上表现一致	不稳定，可能在某些数据集上失败
核心思想	用随机性换取公平性和可分析性	用学习换取对特定数据的最优拟合

所以，C_rand = {Px | x ∈ C} 这个看似简单的公式，实际上是通过一个巧妙的随机化设计，将一个难以分析的启发式问题（如何找到最好的码本）转化为了一个可以在概率论框架下进行严格分析的问题，从而为整个算法的稳定性和高性能奠定了坚实的理论基础。这正是这篇论文RaBitQ: Quantizing High-Dimensional Vectors with a Theoretical Error Bound for Approximate Nearest Neighbor Search最大的亮点。

Reference

RaBitQ：用于近似最近邻搜索的带理论误差界的高维向量量化 https://www.alphaxiv.org/abs/2405.12497
将向量压缩发挥到极致：Milvus 如何利用 RaBitQ 将查询次数提高 3 倍 https://milvus.io/zh/blog/bring-vector-compression-to-the-extreme-how-milvus-serves-3×-more-queries-with-rabitq.md

将向量压缩发挥到极致：Milvus 如何利用 RaBitQ 将查询次数提高 3 倍 ​

RabitQ介绍 ​

传统搜索算法所面临的挑战 ​

Milvus中的RabitQ工程 ​

基准测试 ​

RabitQ底层详解 ​

总体设计 ​

RaBitQ 的思路：一把“公平”的尺子 ​

为什么这个“随机旋转”如此重要？ ​

生动的例子 ​

阶段一：索引阶段 (存储数据) - 整理所有图书并制作索引卡 ​

阶段二：查询阶段 (查找数据) - 当一个读者来查书时 ​

技术细节 ​

第一步：一个“完美”的基础码本 C ​

第二步：一次“公平”的随机旋转 P ​

第三步：牵连的知识及其作用 ​

总结 ​

Reference ​