HNSW算法

1.HNSW的灵感来源：两大核心思想

HNSW的成功，源于它巧妙地结合了两种经典的思想： 1.小世界网络：大家可能听过“六度分隔理论”，意思是地球上任何两个人，平均只需要通过六个中间人就能建立起联系。这就是小世界网络的体现。这种网络的特点是：

高聚类性：你的朋友之间，彼此也很可能互相是朋友（形成聚集的小团体）。
短平均路径：尽管有聚集性，但任意两个节点之间的平均距离却很短。HNSW的目标就是构建一个具有类似特性的图，使得可以从任意节点出发，用很少的“步数”（跳跃）到达目标节点。 2.跳表：想象一本有目录的书。目录就是书的“高层结构”，它章节标题，让你能快速定位到大概范围。然后你翻到对应章节，再通过更细的标题或页码找到具体内容。跳表就是类似的多层索引结构，在数据链表上建立多层“快车道”，从高层粗犷检索开始，逐层细化，直到最底层找到目标，从而避免从头到尾的遍历。 HNSW正是将小世界网络的连通性和跳表的分层思想融合在了一起

2.算法原理分步详解

HNSW（Hierarchical Navigable Small World，分层可导航小世界图）是一种基于图结构的近似最近邻（ANN）搜索算法，
它通过构建一个多层次的“可导航小世界图”，让搜索过程像“在城市地图中找路”一样高效。

其核心思想是：

先在高层图中快速找到大致方向，再在底层图中精确定位目标。

下面我们来分步解析 HNSW 的工作原理。

1.图结构的构建（Index Construction）

HNSW 的核心数据结构是一个多层图（Hierarchical Graph），
每一层都是一个“小世界网络（Small World Graph）”，即节点之间存在较短的路径连接。

步骤 1：多层结构（层级随机化）

每个向量会被随机分配到若干层（Level 0 ~ L）。
层数的分布遵循指数衰减规律（高层节点少，底层节点多）。
例如：
- Level 3：只有少数节点（类似城市的高速公路网）
- Level 2：节点更多（城市主干道）
- Level 1：更密集（区级道路）
- Level 0：所有节点都在这里（街道级别）

这种结构让算法能像缩放地图一样，先看宏观，再聚焦微观。

步骤 2：逐层插入节点（Layer-by-Layer Insertion）

当新向量 v 进入系统时，HNSW 会逐层插入：

确定插入层级
根据随机分配的层级 L_v，决定 v 将出现在哪几层。
自顶向下导航
从当前最高层开始，找到与 v 最近的节点作为“入口点（Entry Point）”。
逐层下降搜索
在每一层中，执行“贪心搜索（Greedy Search）”：
- 不断跳向更接近 v 的邻居；
- 当没有更近的节点时，停止；
- 将当前位置作为下一层的起点。
在对应层建立连接（Linking）
在 v 所在的每一层，选取若干最近邻节点建立边连接（邻居数量由参数 M 控制）。
为保持小世界特性，HNSW 会对邻居集合进行“修剪”，确保网络稀疏且高效。

2.查询阶段（Search Process）

HNSW 的搜索过程与构建阶段类似，同样遵循“自顶向下、逐层逼近”的策略。

步骤 1：从顶层开始搜索

选择一个入口节点（通常是构建时的最高层入口点）。
在最高层使用贪心搜索找到与查询向量 q 最近的节点。

步骤 2：逐层向下导航

将上层搜索到的最优节点作为下一层的入口；
在更低层的图中继续搜索，逐步缩小搜索范围；
每下一层，节点密度增加，搜索精度提升。

步骤 3：底层精确搜索

到达底层（Level 0）后，算法会使用“优先队列 + 局部扩展搜索”策略：
- 维护一个候选节点集合（Candidate List）；
- 扩展其邻居并更新最近邻；
- 重复直到候选集不再变化或达到设定搜索深度（参数 ef_search）。
最终返回距离最近的 K 个节点。

3.关键参数说明

参数	含义	作用
`M`	每个节点的最大邻居数	越大图越稠密，召回率高但内存开销增大
`ef_construction`	构建阶段的搜索宽度	控制索引构建质量与速度
`ef_search`	查询阶段的搜索宽度	值越大，精度越高但搜索时间更长

4.HNSW 的性能特点

高精度：通过层级导航逐步逼近最优解，近似结果非常接近精确搜索；
高效率：图结构使得搜索复杂度接近 O(log N)；
可增量更新：新节点可动态插入，无需重建索引；
内存友好：通过稀疏连接与层级控制，平衡性能与空间。

5. 类比理解

可以把 HNSW 想象成一场“多层地图找目标”的游戏：

层级	类比	搜索作用
顶层	全国高速公路地图	快速确定大致方向
中层	城市主干道地图	精确锁定区域
底层	街区地图	找到具体目标

在搜索过程中，算法像一个熟练的导航员，
从高速公路（高层）出发，逐层进入城区（低层），最终找到目标建筑（最邻近向量）。

✅ 总结：HNSW 的核心思想

分层导航 + 贪心搜索 + 局部连接优化

HNSW 通过在不同层次建立稀疏图结构，使搜索可以先全局定位、再局部精查，
在高维向量检索任务中实现了近似最优的性能与速度平衡。
它已成为当前向量数据库（如 Milvus、FAISS、Weaviate）中默认启用的主流索引算法。

3.HNSW算法实现

🧠 HNSW算法Python实现

3.1我们导入必要的库：

python

import numpy as np
import random
import math
from collections import defaultdict
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import time
from sklearn.metrics.pairwise import euclidean_distances
import warnings
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
from sklearn.metrics.pairwise import euclidean_distances
import time


# 强制设置中文字体，解决中文显示问题
plt.rcParams['font.sans-serif'] = ['PingFang SC', 'Microsoft YaHei', 'SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 设置随机种子以保证结果可重现
np.random.seed(41)

3.2实现简化的HNSW类

python

class SimpleHNSW:
    """简化的HNSW实现，用于学习演示"""
    
    def __init__(self, max_elements=1000, M=10, ef_construction=50, max_layers=6):
        """
        初始化HNSW索引
        
        参数:
        - max_elements: 最大元素数量
        - M: 每个节点的最大连接数
        - ef_construction: 构建时的搜索范围
        - max_layers: 最大层数
        """
        self.max_elements = max_elements
        self.M = M  # 每个节点的最大连接数
        self.ef_construction = ef_construction  # 构建时的搜索范围
        self.max_layers = max_layers  # 最大层数
        
        # 存储所有数据点
        self.data_points = []
        # 每层的图结构（邻接表），每层是一个字典，key是节点ID，value是邻居列表
        self.layers = [defaultdict(list) for _ in range(max_layers)]
        # 全局入口点（最高层的节点）
        self.entry_point = None
        self.entry_level = -1  # 入口点所在的最高层级
        
    def _random_level(self):
        """随机生成节点的层级（指数分布）"""
        level = 0
        while random.random() < 0.5 and level < self.max_layers - 1:
            level += 1
        return level
    
    def _euclidean_distance(self, a, b):
        """计算欧氏距离"""
        return np.sqrt(np.sum((a - b) ** 2))
    
    def _search_layer(self, query, entry_point, ef, layer):
        """
        在指定层搜索最近邻
        
        参数:
        - query: 查询向量
        - entry_point: 搜索起始点
        - ef: 搜索范围（返回的候选点数量）
        - layer: 搜索的层级
        """
        if entry_point is None or entry_point not in self.layers[layer]:
            return []
            
        visited = set([entry_point])
        # 候选集：存储(距离, 节点ID)元组，从入口点开始
        candidates = [(self._euclidean_distance(query, self.data_points[entry_point]), entry_point)]
        # 使用堆来维护候选集（这里简化为列表排序）
        results = []
        
        while candidates and len(results) < ef:
            # 获取距离最近的候选点
            candidates.sort(key=lambda x: x[0])
            current_dist, current_point = candidates.pop(0)
            
            # 检查是否应该将当前点加入结果
            if not results or current_dist < results[-1][0]:
                results.append((current_dist, current_point))
                results.sort(key=lambda x: x[0])  # 保持结果按距离排序
                if len(results) > ef:
                    results = results[:ef]  # 限制结果集大小
            
            # 探索当前点的所有邻居节点
            for neighbor in self.layers[layer][current_point]:
                if neighbor not in visited:
                    visited.add(neighbor)
                    dist = self._euclidean_distance(query, self.data_points[neighbor])
                    candidates.append((dist, neighbor))
        
        return results
    
    def add_point(self, point):
        """
        向HNSW中添加新点
        
        参数:
        - point: 要添加的数据点向量
        """
        if len(self.data_points) >= self.max_elements:
            raise ValueError("达到最大容量")
        
        point_id = len(self.data_points)  # 新点在data_points中的id索引
        self.data_points.append(point)
        
        # 确定新点的层级
        level = self._random_level()
        
        # 如果是第一个点，设为入口点
        if self.entry_point is None:
            self.entry_point = point_id
            self.entry_level = level
            for l in range(level + 1):
                self.layers[l][point_id] = []  # 在新点的每一层创建空邻居列表
            return
        
        # 从最高层开始搜索，找到每层的最近邻
        current_point = self.entry_point
        current_max_level = self.entry_level
        
        # 从顶层开始搜索，找到每层的入口点
        for l in range(current_max_level, level, -1):
            if l < len(self.layers):
                results = self._search_layer(point, current_point, 1, l)
                if results:
                    current_point = results[0][1]  # 更新为最近的点
        
        # 从新点的最高层开始，逐层向下插入并建立连接
        for l in range(min(level, current_max_level), -1, -1):
            # 在当前层搜索ef_construction个最近邻
            results = self._search_layer(point, current_point, self.ef_construction, l)
            
            # 选择前M个最近邻作为连接
            neighbors = [idx for _, idx in results[:self.M]]
            
            # 在新点的当前层创建连接
            self.layers[l][point_id] = neighbors.copy()
            
            # 双向连接：邻居也连接到新点
            for neighbor in neighbors:
                if len(self.layers[l][neighbor]) < self.M:
                    # 邻居连接数未满，直接添加
                    self.layers[l][neighbor].append(point_id)
                else:
                    # 如果邻居连接数已满，替换最远的连接
                    neighbor_neighbors = self.layers[l][neighbor]
                    distances = [self._euclidean_distance(self.data_points[neighbor], 
                                                         self.data_points[n]) for n in neighbor_neighbors]
                    max_idx = np.argmax(distances)  # 找到最远的邻居
                    # 如果新点更近，则替换最远的邻居
                    if self._euclidean_distance(self.data_points[neighbor], point) < distances[max_idx]:
                        neighbor_neighbors[max_idx] = point_id
            
            # 更新当前点用于下一层的搜索
            if results:
                current_point = results[0][1]
        
        # 如果新点的层级比当前入口点高，更新入口点
        if level > self.entry_level:
            self.entry_point = point_id
            self.entry_level = level
    
    def search(self, query, k=5, ef_search=50):
        """
        在HNSW中搜索最近邻
        
        参数:
        - query: 查询向量
        - k: 返回的最近邻数量
        - ef_search: 搜索时的候选集大小（越大精度越高但速度越慢）
        
        返回:
        - 包含(节点ID, 距离)的列表，按距离升序排列
        """
        if self.entry_point is None:
            return []
        
        current_point = self.entry_point
        current_level = self.entry_level
        
        # 从顶层开始搜索
        for l in range(current_level, 0, -1):
            results = self._search_layer(query, current_point, 1, l)
            if results:
                current_point = results[0][1]  # 更新为每层的入口点
        
        # 在最底层进行精细搜索
        results = self._search_layer(query, current_point, ef_search, 0)
        
        # 返回前k个结果
        return [(idx, dist) for dist, idx in results[:k]]

3.3第三步：生成示例数据和可视化函数

python

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
from sklearn.metrics.pairwise import euclidean_distances
import time

# --- 1. 数据生成 ---

def generate_sample_data(n_samples=200, dim=2):
    """生成示例数据：四个分离的高斯分布簇"""
    clusters = []
    
    # 创建四个簇
    cluster1 = np.random.normal(loc=[2, 2], scale=0.3, size=(n_samples//4, dim))
    cluster2 = np.random.normal(loc=[8, 3], scale=0.4, size=(n_samples//4, dim))  
    cluster3 = np.random.normal(loc=[5, 8], scale=0.35, size=(n_samples//4, dim))
    cluster4 = np.random.normal(loc=[3, 6], scale=0.4, size=(n_samples - 3*(n_samples//4), dim))
    
    data = np.vstack([cluster1, cluster2, cluster3, cluster4])
    return data

# --- 2. 可视化部分 ---

def _sort_legend(ax):
    """自动去重并保持绘图顺序"""
    handles, labels = ax.get_legend_handles_labels()
    by_label = dict(zip(labels, handles))
    ax.legend(by_label.values(), by_label.keys(), loc='upper right', fontsize=8)

def _draw_3d_base(ax, hnsw, data, layers, h_gap, query=None):
    """3D视图通用底座"""
    z_max = (max(layers) * h_gap) + 2.0 if layers else 10
    ax.set_axis_off()
    ax.view_init(elev=20, azim=-60)
    ax.set_zlim(0, z_max)
    
    x_min, x_max = data[:, 0].min() - 0.5, data[:, 0].max() + 0.5
    y_min, y_max = data[:, 1].min() - 0.5, data[:, 1].max() + 0.5
    
    # 简单的颜色列表，用于区分层级
    layer_colors = ['#FFFACD', '#98FB98', '#87CEEB', '#DDA0DD', '#F0E68C']
    
    for l in layers:
        z = l * h_gap
        color = layer_colors[l % len(layer_colors)]
        # 平面
        corners = [[x_min, y_min, z], [x_max, y_min, z], [x_max, y_max, z], [x_min, y_max, z]]
        poly = Poly3DCollection([corners], alpha=0.1, facecolor=color)
        ax.add_collection3d(poly)
        # 边框
        for i in range(4):
            ax.plot([corners[i][0], corners[(i+1)%4][0]], [corners[i][1], corners[(i+1)%4][1]], [z, z], 'k-', alpha=0.15, lw=0.8)
        ax.text(x_min, y_min, z, f'Layer {l}', fontsize=9, fontweight='bold', ha='right')
        # 节点
        nodes = list(hnsw.layers[l].keys())
        if nodes:
            pts = data[nodes]
            ax.scatter(pts[:, 0], pts[:, 1], z, c='#888888', s=20, alpha=0.3, edgecolors='none', label='数据点')
        # 查询点投影
        if query is not None:
            ax.scatter(query[0], query[1], z, c='#FFD93D', marker='*', s=100, alpha=0.3, label=None)

# --- 分步绘图函数 ---

def _plot_step_1(ax, data, query):
    """步骤1：绘制原始数据分布"""
    ax.scatter(data[:, 0], data[:, 1], c='lightblue', alpha=0.6, s=30, label='数据点')
    if query is not None: ax.scatter(query[0], query[1], c='#FFD93D', marker='*', s=200, edgecolors='black', label='查询点')
    ax.set_title('1. 原始数据分布'); ax.grid(True, alpha=0.3)

def _plot_step_2(ax, hnsw, data, layers, h_gap, node_levels):
    """步骤2：展示构图逻辑（随机定层 & 邻居连接）"""
    _draw_3d_base(ax, hnsw, data, layers, h_gap)
    target = next((n for n, ls in node_levels.items() if len(ls) >= 2), list(node_levels.keys())[0])
    levels = node_levels.get(target, [])
    for l in layers:
        if l in levels:
            z = l * h_gap
            pt = data[target]
            ax.scatter(pt[0], pt[1], z, c='red', s=100, edgecolors='black', zorder=10, label='新节点')
            nbs = hnsw.layers[l].get(target, [])
            if nbs:
                nb_pts = data[nbs]
                ax.scatter(nb_pts[:, 0], nb_pts[:, 1], z, c='green', s=60, edgecolors='black', zorder=9, label='邻居节点')
                for nb in nb_pts: ax.plot([pt[0], nb[0]], [pt[1], nb[1]], [z, z], c='purple', linewidth=2, zorder=8, label='建立连接')
    ax.set_title('2. 构图逻辑: 随机定层 & 邻居连接')

def _plot_step_3(ax, hnsw, data, layers, h_gap, node_levels):
    """步骤3：HNSW 多层结构概览"""
    _draw_3d_base(ax, hnsw, data, layers, h_gap)
    layer_colors = ['#FFFACD', '#98FB98', '#87CEEB', '#DDA0DD', '#F0E68C']
    for l in layers:
        z = l * h_gap
        nodes = list(hnsw.layers[l].keys())
        if nodes:
            color = layer_colors[l % len(layer_colors)]
            ax.scatter(data[nodes, 0], data[nodes, 1], z, c=[color], edgecolors='black', s=40, alpha=0.8)
            for n in nodes[:20]:
                for nb in hnsw.layers[l][n]:
                    ax.plot([data[n][0], data[nb][0]], [data[n][1], data[nb][1]], [z, z], c='gray', alpha=0.2, lw=0.5)
    for n, ls in list(node_levels.items())[:30]:
        if len(ls) > 1:
            pt = data[n]
            ax.plot([pt[0], pt[0]], [pt[1], pt[1]], [min(ls)*h_gap, max(ls)*h_gap], 'k--', alpha=0.2, lw=0.5, label='跨层连接')
    ax.set_title('3. HNSW 多层结构概览')

def _plot_step_4(ax, hnsw, layers, path):
    """步骤4：分析结构规模与搜索代价"""
    counts = [len(hnsw.layers[l]) for l in layers]
    costs = [0] * len(layers)
    if path:
        for l, p in path.items():
            if l in layers: costs[layers.index(l)] = len(p)
    ax.bar(layers, counts, color='skyblue', alpha=0.6, label='层级节点总数')
    ax2 = ax.twinx()
    ax2.plot(layers, costs, 'r-o', lw=2, label='实际访问节点数')
    ax.set_title('4. 结构规模 vs 搜索代价'); ax.set_xlabel('Layer')
    lines, labels = ax.get_legend_handles_labels()
    l2, lb2 = ax2.get_legend_handles_labels()
    ax.legend(lines+l2, labels+lb2, loc='upper right')

def _plot_step_5(ax, hnsw, data, layers, h_gap, query):
    """步骤5：展示顶层入口点选择"""
    _draw_3d_base(ax, hnsw, data, layers, h_gap, query)
    z_top = max(layers) * h_gap
    entry = data[hnsw.entry_point]
    if query is not None:
        ax.scatter(query[0], query[1], z_top+1.5, c='#FFD93D', marker='*', s=300, edgecolors='black', zorder=20, label='查询点')
        ax.plot([query[0], query[0]], [query[1], query[1]], [0, z_top+1.5], 'k--', alpha=0.2)
        ax.plot([query[0], entry[0]], [query[1], entry[1]], [z_top, z_top], c='orange', ls='--', label='距离指示')
    ax.scatter(entry[0], entry[1], z_top, c='red', marker='v', edgecolors='black', s=200, zorder=20, label='入口点')
    ax.scatter(entry[0], entry[1], z_top, c='red', s=600, alpha=0.2)
    ax.set_title('5. 入口点选择 (Top Layer)')

def _plot_step_6(ax, hnsw, data, layers, h_gap, query, path):
    """步骤6：演示下潜检索过程"""
    _draw_3d_base(ax, hnsw, data, layers, h_gap, query)
    if path and query is not None:
        ax.scatter(query[0], query[1], 0, c='#FFD93D', marker='*', s=0, alpha=0, label='查询点') # Legend hack
        for l, p in path.items():
            z = l * h_gap
            pts = data[p]
            ax.plot(pts[:,0], pts[:,1], [z]*len(pts), c='red', lw=2 if l>0 else 1, label='搜索路径')
            ax.scatter(pts[:,0], pts[:,1], z, c='orange', s=50, edgecolors='black', label='访问节点')
            for n in p[:3]:
                for nb in hnsw.layers[l][n]:
                    nb_pt = data[nb]
                    ax.plot([data[n][0], nb_pt[0]], [data[n][1], nb_pt[1]], [z, z], c='purple', alpha=0.2, label='考察连线')
            if l > 0 and (l-1) in path:
                prev = data[path[l-1][0]]
                ax.plot([pts[-1,0], prev[0]], [pts[-1,1], prev[1]], [z, z-h_gap], c='blue', ls='--', label='层间下潜')
    ax.set_title('6. 下潜检索过程')

def _plot_step_7(ax, hnsw, data, query, path, results, ef=20):
    """步骤7：底层精确搜索 (Layer 0)"""
    l0_nodes = list(hnsw.layers[0].keys())
    ax.scatter(data[l0_nodes, 0], data[l0_nodes, 1], c='#ecf0f1', s=30, label='数据点')
    if path and 0 in path:
        p = path[0]; p_pts = data[p]
        inspected = {nb for n in p for nb in hnsw.layers[0][n]} - set(p)
        if inspected:
            ins_pts = data[list(inspected)]
            ax.scatter(ins_pts[:, 0], ins_pts[:, 1], c='#9b59b6', s=40, alpha=0.5, label='候选邻居')
        for i in range(len(p_pts)-1):
            ax.arrow(p_pts[i,0], p_pts[i,1], p_pts[i+1,0]-p_pts[i,0], p_pts[i+1,1]-p_pts[i,1],
                     head_width=0.2, fc='#e67e22', ec='#e67e22', length_includes_head=True, zorder=5)
        ax.scatter(p_pts[:,0], p_pts[:,1], c='#e67e22', s=60, edgecolors='black', label='移动轨迹', zorder=6)
        ax.scatter(p_pts[0,0], p_pts[0,1], c='red', marker='v', edgecolors='black', s=150, label='Layer 0 入口', zorder=10)
    if query is not None: ax.scatter(query[0], query[1], c='#FFD93D', marker='*', edgecolors='black', s=350, label='查询点')
    if results:
        res_pts = data[[r[0] for r in results]]
        ax.scatter(res_pts[:, 0], res_pts[:, 1], c='red', s=100, marker='o', alpha=0.8, label='HNSW结果')
    ax.set_title(f'7. 底层精搜 (ef={ef})')

def _plot_step_8(ax, data, query, results):
    """步骤8：结果对比与召回率分析"""
    if not results or query is None: return
    k = len(results)
    dists = euclidean_distances([query], data)[0]
    gt_idx = np.argsort(dists)[:k]
    recall = len(set(gt_idx) & set([r[0] for r in results])) / k
    ax.scatter(data[:, 0], data[:, 1], c='lightgray', s=30, alpha=0.3, label='数据点')
    ax.scatter(data[gt_idx, 0], data[gt_idx, 1], edgecolors='green', facecolors='none', linewidth=2.5, marker='s', label='暴力搜索 (GT)')
    res_pts = data[[r[0] for r in results]]
    ax.scatter(res_pts[:, 0], res_pts[:, 1], c='red', s=100, marker='o', alpha=0.8, label='HNSW结果')
    ax.scatter(query[0], query[1], c='#FFD93D', marker='*', edgecolors='black', s=300, label='查询点')
    missed = set(gt_idx) - set([r[0] for r in results])
    for idx in missed:
        pt = data[idx]
        ax.plot([query[0], pt[0]], [query[1], pt[1]], c='red', ls='--', alpha=0.6)
        ax.text(pt[0], pt[1], "漏检", color='red', fontweight='bold')
    ax.set_title(f'8. 结果对比 (召回率: {recall:.1%})')

def visualize_hnsw(hnsw, query_point=None, results=None, search_path=None):
    """简化后的可视化入口函数"""
    if not hnsw.data_points: return
    data = np.array(hnsw.data_points)
    layers = sorted([l for l in range(hnsw.max_layers) if hnsw.layers[l]])
    node_levels = {}
    for l in layers:
        for n in hnsw.layers[l]: node_levels.setdefault(n, []).append(l)
    h_gap = 2.0
    
    fig = plt.figure(figsize=(24, 12))
    layout = [(1, False), (2, True), (3, True), (4, False), (5, True), (6, True), (7, False), (8, False)]
    axes = [fig.add_subplot(2, 4, i, projection='3d' if is3d else None) for i, is3d in layout]
    
    _plot_step_1(axes[0], data, query_point)
    _plot_step_2(axes[1], hnsw, data, layers, h_gap, node_levels)
    _plot_step_3(axes[2], hnsw, data, layers, h_gap, node_levels)
    _plot_step_4(axes[3], hnsw, layers, search_path)
    _plot_step_5(axes[4], hnsw, data, layers, h_gap, query_point)
    _plot_step_6(axes[5], hnsw, data, layers, h_gap, query_point, search_path)
    _plot_step_7(axes[6], hnsw, data, query_point, search_path, results)
    _plot_step_8(axes[7], data, query_point, results)
    
    for ax in axes: _sort_legend(ax)
    plt.tight_layout(); plt.show()

# --- 3. 性能演示 ---

def demonstrate_hnsw_performance():
    """演示HNSW性能对比"""
    print("=" * 60)
    print("HNSW算法性能演示")
    print("=" * 60)
    
    # 生成测试数据
    data = generate_sample_data(500, 2)
    print(f"生成{len(data)}个二维数据点")
    
    # 创建HNSW索引
    hnsw = SimpleHNSW(max_elements=1000, M=10, ef_construction=50, max_layers=5)
    
    # 批量添加数据
    print("构建HNSW索引...")
    start_time = time.time()
    for i, point in enumerate(data):
        hnsw.add_point(point)
        if (i + 1) % 100 == 0:
            print(f"已添加{i + 1}个点")
    
    construction_time = time.time() - start_time
    print(f"HNSW索引构建完成，耗时: {construction_time:.4f}秒")
    
    # 选择查询点
    query_point = np.array([5.0, 5.0])
    print(f"\n查询点: {query_point}")
    
    # 使用HNSW搜索
    start_time = time.time()
    hnsw_results, search_path = hnsw.search_with_path(query_point, k=5, ef_search=30)
    hnsw_time = time.time() - start_time
    
    # 暴力搜索作为基准
    start_time = time.time()
    distances = euclidean_distances([query_point], data)[0]
    bf_indices = np.argsort(distances)[:5]
    bf_distances = distances[bf_indices]
    bf_time = time.time() - start_time
    
    # 显示结果对比
    print(f"\n搜索结果对比:")
    print(f"HNSW搜索 - 找到{len(hnsw_results)}个最近邻, 耗时: {hnsw_time:.6f}秒")
    print(f"暴力搜索 - 找到{len(bf_indices)}个最近邻, 耗时: {bf_time:.6f}秒")
    
    print(f"\n速度提升: {bf_time/hnsw_time:.2f}倍")
    
    print(f"\nHNSW结果索引: {[idx for idx, _ in hnsw_results]}")
    print(f"HNSW结果距离: {[dist for _, dist in hnsw_results]}")
    print(f"暴力搜索结果索引: {bf_indices}")
    print(f"暴力搜索结果距离: {bf_distances}")
    
    # 检查召回率
    hnsw_indices_set = set(idx for idx, _ in hnsw_results)
    bf_indices_set = set(bf_indices)
    intersection = hnsw_indices_set & bf_indices_set
    recall = len(intersection) / len(bf_indices_set)
    print(f"召回率: {recall:.2%} ({len(intersection)}/{len(bf_indices_set)})")
    
    return hnsw, data, query_point, hnsw_results, bf_indices, search_path

# 1. 运行标准演示
hnsw, data, query, hnsw_results, bf_results, search_path = demonstrate_hnsw_performance()

# 2. 调用可视化
visualize_hnsw(hnsw, query, hnsw_results, search_path)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287

输出结果

text

============================================================
HNSW算法性能演示
============================================================
生成500个二维数据点
构建HNSW索引...
已添加100个点
已添加200个点
已添加300个点
已添加400个点
已添加500个点
HNSW索引构建完成，耗时: 0.8465秒

查询点: [5. 5.]

搜索结果对比:
HNSW搜索 - 找到5个最近邻, 耗时: 0.000873秒
暴力搜索 - 找到5个最近邻, 耗时: 0.002740秒

速度提升: 3.14倍

HNSW结果索引: [413, 388, 432, 455, 469]
HNSW结果距离: [np.float64(1.2234940484615728), np.float64(1.415148522001549), np.float64(1.468755986770868), np.float64(1.4742594766534751), np.float64(1.5156054576554492)]
暴力搜索结果索引: [413 388 432 455 469]
暴力搜索结果距离: [1.22349405 1.41514852 1.46875599 1.47425948 1.51560546]
召回率: 100.00% (5/5)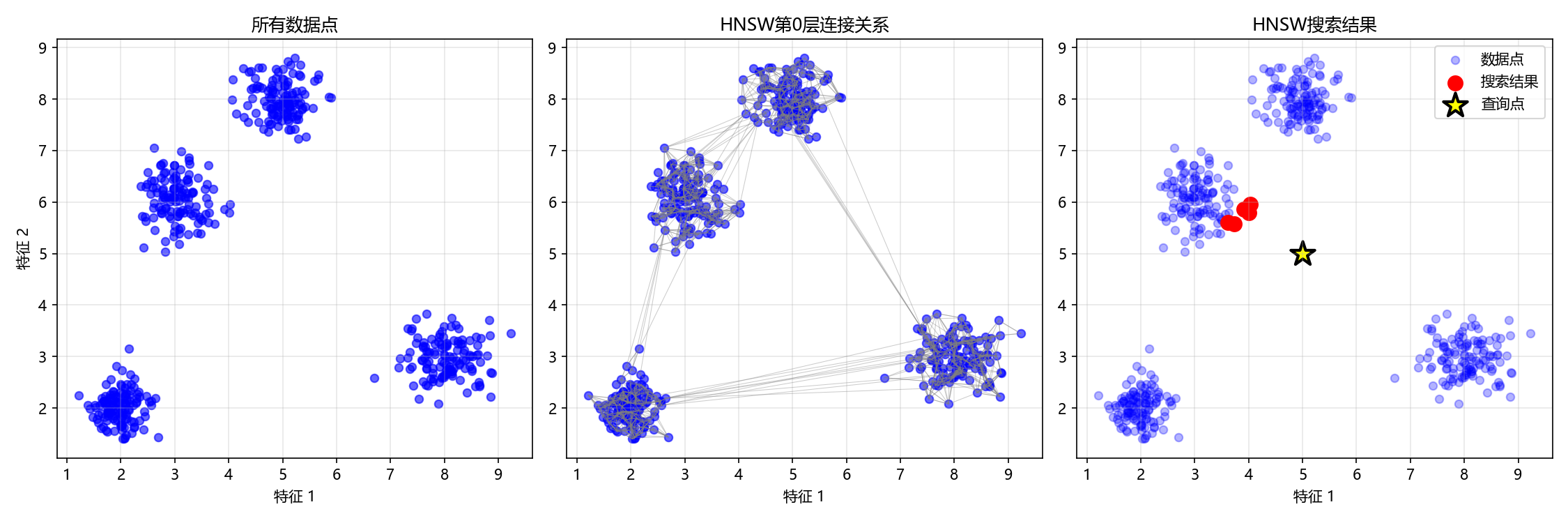

alt text

3.4参数影响分析

python

def analyze_hnsw_parameters():
    """分析HNSW参数对性能的影响"""
    data = generate_sample_data(1000, 2)
    query = np.array([5.0, 5.0])
    
    # 测试不同参数组合
    parameter_combinations = [
        {'M': 5, 'ef_construction': 30, 'ef_search': 20},
        {'M': 10, 'ef_construction': 50, 'ef_search': 30},
        {'M': 15, 'ef_construction': 100, 'ef_search': 50}
    ]
    
    results = []
    
    for i, params in enumerate(parameter_combinations):
        print(f"\n测试参数组合 {i+1}: M={params['M']}, ef_construction={params['ef_construction']}")
        
        # 构建HNSW索引
        hnsw = SimpleHNSW(max_elements=2000, M=params['M'], 
                         ef_construction=params['ef_construction'], max_layers=6)
        
        start_time = time.time()
        for point in data:
            hnsw.add_point(point)
        build_time = time.time() - start_time
        
        # 搜索
        start_time = time.time()
        hnsw_results = hnsw.search(query, k=5, ef_search=params['ef_search'])
        search_time = time.time() - start_time
        
        # 计算召回率
        distances = euclidean_distances([query], data)[0]
        bf_indices = np.argsort(distances)[:5]
        hnsw_indices_set = set(idx for idx, _ in hnsw_results)
        recall = len(hnsw_indices_set & set(bf_indices)) / 5
        
        results.append({
            'params': params,
            'build_time': build_time,
            'search_time': search_time,
            'recall': recall
        })
        
        print(f"构建时间: {build_time:.4f}秒, 搜索时间: {search_time:.6f}秒, 召回率: {recall:.2%}")
    
    return results

# 运行参数分析
param_results = analyze_hnsw_parameters()

输出结果

text

试参数组合 1: M=5, ef_construction=30
构建时间: 1.2516秒, 搜索时间: 0.000374秒, 召回率: 0.00%

测试参数组合 2: M=10, ef_construction=50
构建时间: 3.2875秒, 搜索时间: 0.000824秒, 召回率: 100.00%

测试参数组合 3: M=15, ef_construction=100
构建时间: 3.8578秒, 搜索时间: 0.001488秒, 召回率: 100.00%

核心参数的作用与结果分析

首先，理解两个核心参数的作用至关重要：

M（最大连接数）：决定了图中每个节点可以和多少个邻居建立连接。M值越大，图的连通性越好，导航路径越多，但也会使索引更复杂、更占内存。
ef_construction（构建时候选集大小）：控制着在插入一个新节点时，算法会在每一层探索多少个候选邻居来寻找最佳连接。此值越大，构建出的图质量通常越高，搜索精度越有保障，但索引的构建时间也会相应增加

现在我来尝试分析一下结果：

组合1 (M=5, ef_construction=30)：构建最快，但召回率崩溃
- 这是典型的参数设置过于激进导致的问题。过小的 M和 ef_construction使得构建出的图结构连通性极差。搜索时，算法可能迅速陷入局部最优解而无法找到真实的最近邻，从而导致召回率为0。虽然它的构建和搜索速度最快，但无法返回正确结果，这个组合在实际应用中是不可用的。
组合2 (M=10, ef_construction=50)：性能的“甜蜜点”
- 此组合在构建时间、搜索速度和召回率之间取得了极佳的平衡。它将 M和 ef_construction提升到合理水平，成功构建出一个高质量的图结构，实现了100%的召回率。其搜索速度依然非常快，仅比组合1慢约0.00045秒，这个时间差对于大多数应用来说微不足道，却换来了结果准确性的质的飞跃。
*组合3 (M=15, ef_construction=100)：精度优先，资源消耗增大
- 进一步增大参数带来了边际效益递减。召回率维持在100%，但构建时间和搜索时间都有显著增加。这是因为算法需要处理更多的连接和候选点。这个组合适用于对召回率有极致要求且可以接受稍长延迟的场景

HNSW算法 ​

1.HNSW的灵感来源：两大核心思想 ​

2.算法原理分步详解​ ​

1.图结构的构建（Index Construction） ​

步骤 1：多层结构（层级随机化） ​

步骤 2：逐层插入节点（Layer-by-Layer Insertion） ​

2.查询阶段（Search Process） ​

步骤 1：从顶层开始搜索 ​

步骤 2：逐层向下导航 ​

步骤 3：底层精确搜索 ​

3.关键参数说明 ​

4.HNSW 的性能特点 ​

5. 类比理解 ​

3.HNSW算法实现 ​

3.1我们导入必要的库： ​

3.2实现简化的HNSW类 ​

3.3第三步：生成示例数据和可视化函数 ​

3.4参数影响分析 ​

HNSW算法

1.HNSW的灵感来源：两大核心思想

2.算法原理分步详解

1.图结构的构建（Index Construction）

步骤 1：多层结构（层级随机化）

步骤 2：逐层插入节点（Layer-by-Layer Insertion）

2.查询阶段（Search Process）

步骤 1：从顶层开始搜索

步骤 2：逐层向下导航

步骤 3：底层精确搜索

3.关键参数说明

4.HNSW 的性能特点

5. 类比理解

3.HNSW算法实现

3.1我们导入必要的库：

3.2实现简化的HNSW类

3.3第三步：生成示例数据和可视化函数

3.4参数影响分析