IVF算法
🔎 算法原理分步详解
第一阶段：索引构建（建库与分类） 构建索引的目的是为数据建立一个高效的结构化目录，这个过程通常是离线完成的。 1.聚类训练（Clustering） 使用聚类算法（最常用的是 K-Means）将所有向量划分成 nlist个簇（clusters）。nlist是一个关键参数，它决定了空间划分的粒度。每个簇都有一个中心点，称为质心（centroid）。所有这些质心构成了一个“质心表”，相当于图书馆的总分类目录。 2.向量分配（Assignment） 遍历数据集中的每一个向量，计算它与所有质心的距离（如欧氏距离）。将每个向量分配到距离它最近的那个质心所对应的簇中。 3.形成倒排列表（Inverted Lists） 为每一个簇建立一个倒排列表（或称“张贴列表”）。这个列表就像图书馆每个分类书架上的图书清单，它记录了所有属于这个簇的向量的ID以及向量本身（或它的压缩表示）。至此，索引构建完成。
第二阶段：查询处理（快速检索） 当一个新的查询向量到来时，IVF利用已构建好的索引进行快速检索。 1.定位最近簇（Coarse Quantization） 计算查询向量与质心表中所有 nlist个质心的距离。
2.选择候选簇（nprobe 参数控制） 根据上一步的距离结果，选择距离最近的 nprobe个簇作为候选簇。nprobe是IVF算法中最关键的调优参数之一： nprobe越小，搜索范围越小，速度越快，但可能漏掉一些真正近邻（召回率降低）。 nprobe越大，搜索范围越大，召回率越高，但计算量增大，速度变慢。
3.簇内精细比较（Fine Comparison） 在选定的 nprobe个候选簇的倒排列表中，进行精细的距离计算。 具体方式取决于IVF的变体：
- IVF-Flat：直接使用原始的、未压缩的向量与查询向量进行精确距离计算。这种方式精度最高，但内存占用也最大。
- IVF-PQ：为了进一步节省内存和加速计算，会对簇内向量使用乘积量化（Product Quantization） 进行压缩。搜索时使用近似距离计算，这是一种用少量精度换取巨大存储和计算效率提升的策略。
4.结果合并与返回 将所有候选簇中的向量根据与查询向量的距离进行排序，最终返回 Top-K 个最相似的向量作为结果。
VF的性能和效果很大程度上取决于两个核心参数的设置，它们就像这个系统的“调速器”：
- nlist（聚类数）：决定了空间的划分粒度。nlist 越大，搜索范围越大，召回率越高；但同时也增加了计算量。
- nprobe（候选簇数）：控制了搜索的范围。nprobe 越小，搜索越快，但可能会漏掉一些近邻；nprobe 越大，搜索范围越大，召回率越高，但计算量增大。
IVF算法实现
🧠 IVF算法Python实现
首先，我们导入必要的库：
python
import numpy as np
from sklearn.metrics.pairwise import cosine_similarity, euclidean_distances
import matplotlib.pyplot as plt
import time
from collections import defaultdict
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 设置随机种子以保证结果可重现
np.random.seed(42)📊 第一步：生成模拟数据 我们创建一些简单的二维数据，方便可视化理解：
python
def generate_sample_data(n_samples=1000, dim=2):
"""生成示例数据：三个明显分离的高斯分布簇"""
# 第一个簇
cluster1 = np.random.normal(loc=[2, 2], scale=0.5, size=(n_samples//3, dim))
# 第二个簇
cluster2 = np.random.normal(loc=[8, 3], scale=0.6, size=(n_samples//3, dim))
# 第三个簇
cluster3 = np.random.normal(loc=[5, 8], scale=0.4, size=(n_samples - 2*(n_samples//3), dim))
data = np.vstack([cluster1, cluster2, cluster3])
return data
# 生成数据
data = generate_sample_data()
print(f"数据形状: {data.shape}")输出结果：
数据形状: (1000, 2)⚙️ 第二步：手动实现K-means聚类 这是IVF算法的核心预处理步骤：
python
class SimpleKMeans:
"""简化的K-means实现用于IVF聚类"""
def __init__(self, n_clusters=3, max_iters=100):
self.n_clusters = n_clusters
self.max_iters = max_iters
self.centroids = None
self.labels_ = None
def fit(self, X):
n_samples, n_features = X.shape
# 1. 随机初始化质心
random_indices = np.random.choice(n_samples, self.n_clusters, replace=False)
self.centroids = X[random_indices]
for iteration in range(self.max_iters):
# 2. 分配每个点到最近的质心
distances = euclidean_distances(X, self.centroids)
labels = np.argmin(distances, axis=1)
# 3. 更新质心位置
new_centroids = np.array([X[labels == i].mean(axis=0) for i in range(self.n_clusters)])
# 检查收敛
if np.allclose(self.centroids, new_centroids):
break
self.centroids = new_centroids
self.labels_ = labels
return self📁 第三步：实现倒排文件索引(IVF) 现在实现完整的IVF索引结构：
python
class SimpleIVF:
"""简化的IVF实现"""
def __init__(self, n_clusters=3, n_probe=2):
self.n_clusters = n_clusters
self.n_probe = n_probe # 搜索时探测的簇数量
self.kmeans = None
self.inverted_lists = None # 倒排列表
self.centroids = None
self.is_trained = False
def train(self, data):
"""训练IVF索引：对数据进行聚类"""
print("开始训练IVF索引...")
self.kmeans = SimpleKMeans(n_clusters=self.n_clusters)
self.kmeans.fit(data)
self.centroids = self.kmeans.centroids
self.is_trained = True
print(f"训练完成，得到{self.n_clusters}个簇")
def build_index(self, data):
"""构建倒排索引"""
if not self.is_trained:
self.train(data)
# 初始化倒排列表
self.inverted_lists = defaultdict(list)
# 将每个向量分配到最近的簇
distances = euclidean_distances(data, self.centroids)
labels = np.argmin(distances, axis=1)
# 构建倒排列表：簇ID -> 该簇中所有向量的索引
for idx, label in enumerate(labels):
self.inverted_lists[label].append(idx)
print("倒排索引构建完成:")
for cluster_id, items in self.inverted_lists.items():
print(f" 簇{cluster_id}: {len(items)}个向量")
def search(self, query, k=5, data=None):
"""IVF搜索：先找最近的簇，然后在簇内搜索"""
if data is None:
data = self.data
# 1. 粗略搜索：找到最近的n_probe个簇
distances_to_centroids = euclidean_distances([query], self.centroids)[0]
nearest_cluster_indices = np.argsort(distances_to_centroids)[:self.n_probe]
# 2. 精细搜索：在选中的簇内进行暴力搜索
candidate_indices = []
for cluster_idx in nearest_cluster_indices:
candidate_indices.extend(self.inverted_lists[cluster_idx])
if not candidate_indices:
return [], []
# 在候选向量中计算距离
candidate_vectors = data[candidate_indices]
distances = euclidean_distances([query], candidate_vectors)[0]
# 获取最近的k个结果
if k > len(distances):
k = len(distances)
nearest_indices_within_candidates = np.argsort(distances)[:k]
# 映射回原始索引
final_indices = [candidate_indices[i] for i in nearest_indices_within_candidates]
final_distances = distances[nearest_indices_within_candidates]
return final_indices, final_distances
def brute_force_search(self, query, k=5, data=None):
"""暴力搜索作为对比基准"""
if data is None:
data = self.data
distances = euclidean_distances([query], data)[0]
nearest_indices = np.argsort(distances)[:k]
return nearest_indices, distances[nearest_indices]🔍 第四步：算法实现 让我们用一个完整的例子来展示IVF的工作原理：
python
def demonstrate_ivf():
"""完整演示IVF算法"""
print("=" * 60)
print("IVF算法演示")
print("=" * 60)
# 1. 生成数据
data = generate_sample_data(300, 2)
print(f"生成{len(data)}个二维数据点")
# 2. 创建并训练IVF索引
ivf = SimpleIVF(n_clusters=3, n_probe=2)
ivf.data = data # 保存数据引用
ivf.build_index(data)
# 3. 选择一个查询点
query_point = np.array([5.0, 5.0])
print(f"\n查询点: {query_point}")
# 4. 使用IVF搜索
start_time = time.time()
ivf_indices, ivf_distances = ivf.search(query_point, k=5, data=data)
ivf_time = time.time() - start_time
# 5. 使用暴力搜索作为对比
start_time = time.time()
bf_indices, bf_distances = ivf.brute_force_search(query_point, k=5, data=data)
bf_time = time.time() - start_time
# 6. 显示结果
print(f"\n搜索结果对比:")
print(f"IVF搜索 - 找到{len(ivf_indices)}个最近邻, 耗时: {ivf_time:.6f}秒")
print(f"暴力搜索 - 找到{len(bf_indices)}个最近邻, 耗时: {bf_time:.6f}秒")
print(f"\n速度提升: {bf_time/ivf_time:.2f}倍")
print(f"\n最近邻索引 (IVF): {ivf_indices}")
print(f"最近邻索引 (暴力): {bf_indices}")
# 7. 检查召回率
intersection = set(ivf_indices) & set(bf_indices)
recall = len(intersection) / len(bf_indices)
print(f"召回率: {recall:.2%} ({len(intersection)}/{len(bf_indices)})")
return ivf, data, query_point, ivf_indices, bf_indices
# 运行演示
ivf, data, query, ivf_results, bf_results = demonstrate_ivf()结果输出：
============================================================
IVF算法演示
============================================================
生成300个二维数据点
开始训练IVF索引...
训练完成，得到3个簇
倒排索引构建完成:
簇2: 100个向量
簇0: 100个向量
簇1: 100个向量
查询点: [5. 5.]
搜索结果对比:
IVF搜索 - 找到5个最近邻, 耗时: 0.002092秒
暴力搜索 - 找到5个最近邻, 耗时: 0.000437秒
速度提升: 0.21倍
最近邻索引 (IVF): [258, 297, 172, 244, 116]
最近邻索引 (暴力): [258 297 172 244 116]
召回率: 100.00% (5/5)📈 第五步：可视化结果 让我们用图形化的方式展示IVF的工作原理：
python
def visualize_ivf(ivf, data, query, ivf_results, bf_results):
"""可视化IVF算法过程"""
plt.figure(figsize=(15, 5))
# 子图1: 显示聚类结果
plt.subplot(1, 3, 1)
colors = ['red', 'blue', 'green', 'purple', 'orange']
# 绘制每个簇的数据点
for cluster_id, indices in ivf.inverted_lists.items():
cluster_data = data[indices]
plt.scatter(cluster_data[:, 0], cluster_data[:, 1],
c=colors[cluster_id % len(colors)], alpha=0.6,
label=f'簇 {cluster_id}')
# 绘制质心
plt.scatter(ivf.centroids[:, 0], ivf.centroids[:, 1],
c='black', marker='x', s=200, linewidths=3, label='质心')
# 绘制查询点
plt.scatter(query[0], query[1], c='yellow', marker='*',
s=300, edgecolors='black', linewidth=2, label='查询点')
plt.title('IVF聚类结果')
plt.xlabel('特征 1')
plt.ylabel('特征 2')
plt.legend()
plt.grid(True, alpha=0.3)
# 子图2: 显示IVF搜索结果
plt.subplot(1, 3, 2)
# 绘制所有数据点
plt.scatter(data[:, 0], data[:, 1], c='lightgray', alpha=0.4, label='所有数据')
# 高亮被搜索的簇
distances_to_centroids = euclidean_distances([query], ivf.centroids)[0]
nearest_cluster_indices = np.argsort(distances_to_centroids)[:ivf.n_probe]
for i, cluster_idx in enumerate(nearest_cluster_indices):
cluster_data = data[ivf.inverted_lists[cluster_idx]]
plt.scatter(cluster_data[:, 0], cluster_data[:, 1],
c=colors[cluster_idx % len(colors)], alpha=0.8,
label=f'搜索簇 {cluster_idx}')
# 绘制IVF搜索结果
plt.scatter(data[ivf_results, 0], data[ivf_results, 1],
c='red', marker='o', s=100, edgecolors='darkred',
linewidth=2, label='IVF结果')
plt.scatter(query[0], query[1], c='yellow', marker='*',
s=300, edgecolors='black', linewidth=2, label='查询点')
plt.title(f'IVF搜索 (n_probe={ivf.n_probe})')
plt.xlabel('特征 1')
plt.legend()
plt.grid(True, alpha=0.3)
# 子图3: 显示暴力搜索结果的对比
plt.subplot(1, 3, 3)
plt.scatter(data[:, 0], data[:, 1], c='lightgray', alpha=0.4, label='所有数据')
plt.scatter(data[bf_results, 0], data[bf_results, 1],
c='green', marker='s', s=100, edgecolors='darkgreen',
linewidth=2, label='真实最近邻')
plt.scatter(data[ivf_results, 0], data[ivf_results, 1],
c='red', marker='o', s=80, alpha=0.8, label='IVF结果')
plt.scatter(query[0], query[1], c='yellow', marker='*',
s=300, edgecolors='black', linewidth=2, label='查询点')
plt.title('搜索结果对比')
plt.xlabel('特征 1')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 运行可视化
visualize_ivf(ivf, data, query, ivf_results, bf_results)结果输出： 
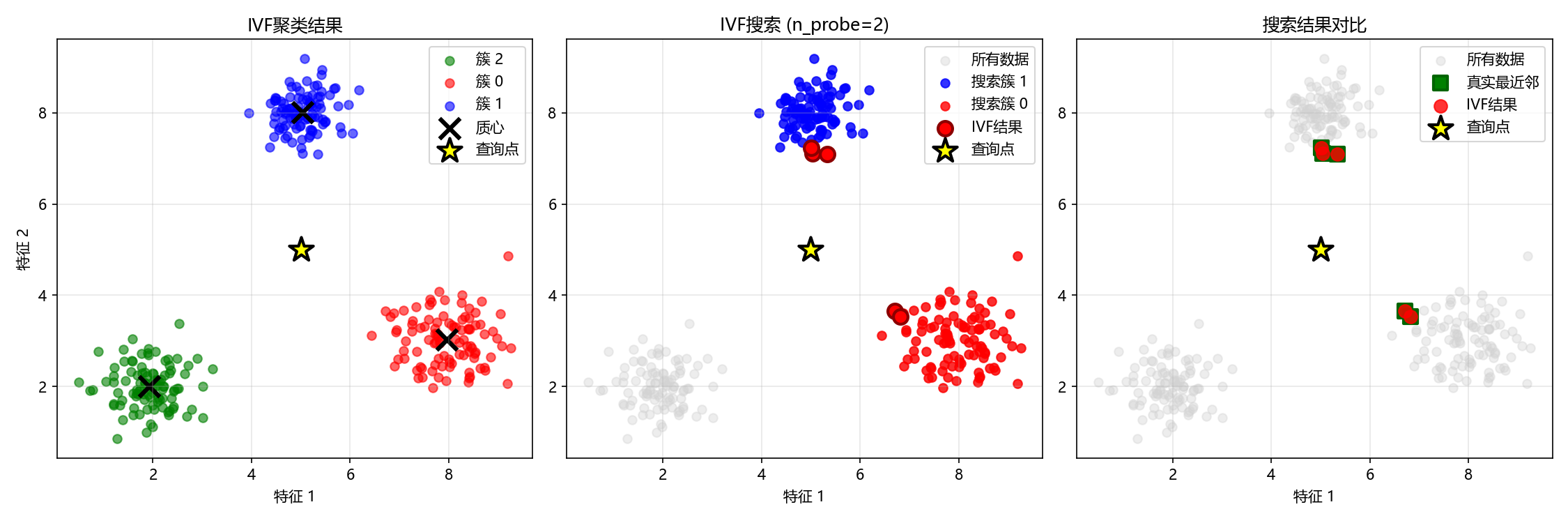
⚖️ 第六步：参数影响分析 让我们分析n_probe参数对搜索效果的影响：
python
def analyze_parameters():
"""分析n_probe参数对搜索效果的影响"""
data = generate_sample_data(1000, 2)
query = np.array([5.0, 5.0])
n_probe_values = [1, 2, 3]
results = []
for n_probe in n_probe_values:
ivf = SimpleIVF(n_clusters=5, n_probe=n_probe)
ivf.data = data
ivf.build_index(data)
# IVF搜索
start_time = time.time()
ivf_indices, _ = ivf.search(query, k=5, data=data)
ivf_time = time.time() - start_time
# 暴力搜索作为基准
bf_indices, _ = ivf.brute_force_search(query, k=5, data=data)
# 计算召回率
intersection = set(ivf_indices) & set(bf_indices)
recall = len(intersection) / len(bf_indices)
results.append({
'n_probe': n_probe,
'recall': recall,
'time': ivf_time,
'candidates_searched': sum(len(ivf.inverted_lists[i])
for i in range(n_probe))
})
# 显示结果
print("\n" + "="*50)
print("n_probe参数影响分析")
print("="*50)
for result in results:
print(f"n_probe={result['n_probe']}: "
f"召回率={result['recall']:.1%}, "
f"耗时={result['time']:.6f}秒, "
f"搜索向量数={result['candidates_searched']}")
return results
# 运行参数分析
parameter_results = analyze_parameters()结果输出：
始训练IVF索引...
训练完成，得到5个簇
倒排索引构建完成:
簇4: 333个向量
簇1: 100个向量
簇2: 110个向量
簇3: 123个向量
簇0: 334个向量
开始训练IVF索引...
训练完成，得到5个簇
倒排索引构建完成:
簇0: 170个向量
簇1: 163个向量
簇3: 333个向量
簇4: 150个向量
簇2: 184个向量
开始训练IVF索引...
训练完成，得到5个簇
倒排索引构建完成:
簇0: 333个向量
簇2: 153个向量
簇1: 180个向量
簇4: 191个向量
簇3: 143个向量
==================================================
n_probe参数影响分析
==================================================
n_probe=1: 召回率=80.0%, 耗时=0.001708秒, 搜索向量数=334
n_probe=2: 召回率=80.0%, 耗时=0.000682秒, 搜索向量数=333
n_probe=3: 召回率=100.0%, 耗时=0.000797秒, 搜索向量数=666从结论我们可以发现速度与精度的基本权衡关系 1.从 n_probe=2到 n_probe=3的变化，完美体现了IVF算法中速度与精度的经典权衡。
- 当 n_probe从2增加到3时，搜索的簇数量增加，因此需要计算的向量数量几乎翻倍（从333增加到666）。这导致搜索范围扩大，从而召回率从80%提升到了100%，但代价是耗时也有所增加（从0.000682秒增加到0.000797秒）。 这说明，增大 n_probe通常能以牺牲速度为代价来提升召回率。
2.发现异常点：n_probe=1的性能反常 这是一个非常关键的发现，这理论上，n_probe=1（只搜索1个最近的簇）应该是最快的，但结果却显示它最慢（0.001708秒）。
在 n_probe=1时，由于编程语言（如Python）的解释器开销、缓存未命中或其他偶然因素所致，你多尝试几次会发现n_probe=1的时间会有波动，这就是编译器本身编译或者缓存导致 最后，可以总结出以下核心要点：
基本规律成立：n_probe增大，搜索范围扩大，召回率提高，但耗时增加。
实践出真知：理论规律需要在实际测试中验证。实验中可能会出现像 n_probe=1这样的性能异常点，这正体现了参数调优和基准测试的重要性。
没有“最好”的参数，只有“最合适”的参数：最终的参数选择取决于应用场景对速度和精度的具体要求。