Annoy算法

1. Annoy的灵感来源与核心思想

Annoy（Approximate Nearest Neighbors Oh Yeah）是由 Spotify 开发的一个高性能近似最近邻搜索库，其核心数据结构是随机投影树（Random Projection Trees）。

Annoy的设计目标非常明确：

低内存占用：索引可以通过内存映射（mmap）方式加载，多个进程可以共享同一份索引，极大降低内存开销
高查询速度：通过树结构快速缩小搜索范围
易于使用：简单的API，便于集成到生产系统

核心思想

通过多棵随机构建的二叉树，将高维空间递归分割成越来越小的区域，相似的向量会大概率被分到同一个叶子节点。

Annoy的成功源于两个关键思想：

1. 随机投影树（Random Projection Trees）

想象你在一个拥挤的图书馆里找书：

不是按照作者、主题等固定规则分类（那样需要完美的分类标准）
而是随机选择两本书作为"锚点"，然后把其他书按"更接近哪本锚点书"分成两堆
重复这个过程，每次在一堆书中再选两本做锚点，继续二分
最终，相似的书会自然地聚在一起

这就是Annoy的核心：用随机超平面递归地二分空间。

2. 森林策略（Forest of Trees）

单棵随机树可能会"运气不好"，把相似的向量分开。怎么办？

建立多棵树（就像多次用不同的随机方式整理图书馆）
查询时在所有树中搜索，合并候选结果
只要有一棵树把相似向量分到一起，就能找到它们

这种"用多次随机尝试提高成功率"的思想，在机器学习中叫做集成学习（Ensemble Learning）。

2. 算法原理分步详解

Annoy（Random Projection Tree Forest）是一种基于二叉树森林的近似最近邻搜索算法。
它通过构建多棵随机投影树，将高维向量空间递归分割，使相似向量大概率落入同一叶节点。

其核心思想是：

先用树结构快速定位到查询向量附近的小区域，再在候选区域内精确计算距离。

下面我们来分步解析 Annoy 的工作原理。

1. 树的构建（Index Construction）

Annoy 的核心数据结构是二叉树森林（多棵独立的二叉树）。
每棵树通过随机投影的方式递归地将空间分割成两半。

步骤 1：随机选择分割超平面

对于当前节点包含的向量集合：

随机选择两个向量 ( v_1 ) 和 ( v_2 )（这两个向量称为"锚点"）
计算中垂超平面：这个超平面将空间分成两半
- 超平面过 ( v_1 ) 和 ( v_2 ) 的中点
- 超平面的法向量是 ( v_1 - v_2 )

这个超平面就像一把"随机的刀"，把当前空间切成两半。

步骤 2：递归分割空间

根据向量在超平面的哪一侧，将向量集合分成两个子集：

左子树：包含所有在超平面"左侧"的向量
右子树：包含所有在超平面"右侧"的向量

递归地对每个子集重复上述过程，直到满足停止条件：

当前节点包含的向量数量 ≤ 设定阈值（如 K=5）
达到最大树深度

此时，当前节点变成叶子节点，存储这些向量的索引。

步骤 3：构建多棵树（森林）

由于单棵树的分割是随机的，可能会：

"运气不好"把相似的向量分开
导致查询时漏掉真正的近邻

解决方案：构建 n_trees 棵独立的树，每棵树用不同的随机种子。

树越多，找到真实近邻的概率越高
但构建时间和内存占用也会增加

2. 查询阶段（Search Process）

给定查询向量 ( q )，Annoy 使用树结构快速定位候选向量。

步骤 1：在每棵树中向下遍历

对于森林中的每棵树：

从根节点开始
在每个内部节点，判断 ( q ) 在分割超平面的哪一侧
根据判断结果，递归进入左子树或右子树
到达叶子节点后，收集该叶子节点中的所有向量索引

这个过程非常快，复杂度是 ( O(\log N) )，其中 ( N ) 是向量总数。

步骤 2：合并候选集

将所有树中收集到的向量索引合并，去重，得到候选集。

候选集的大小由参数 search_k 控制：

search_k 越大，搜索的叶子节点越多
召回率越高，但查询时间也越长

步骤 3：精确计算距离并返回 Top-K

对候选集中的每个向量，计算与查询向量 ( q ) 的真实距离（如欧氏距离或余弦距离）。

按距离排序，返回最近的 K 个向量。

3. 关键参数说明

参数	含义	作用
`n_trees`	构建的树的数量	越大召回率越高，但构建时间和内存占用增加
`search_k`	查询时检查的节点数量	越大召回率越高，但查询时间越长
`K`（叶子大小）	叶子节点最多包含的向量数	越小树越深，查询越精确但构建越慢

4. Annoy 的性能特点

构建速度快：随机分割，无需复杂的聚类或优化
内存友好：索引可以 mmap，多进程共享
查询速度快：树结构使搜索复杂度为 ( O(\log N) )
易于调参：只有两个主要参数（n_trees 和 search_k）

5. 类比理解

可以把 Annoy 想象成一个"快速查字典"的游戏：

类比	Annoy 对应概念
字典按首字母分成26个部分	根节点的第一次二分
每个部分再按第二个字母细分	继续递归二分
最终定位到具体页码	到达叶子节点
用多本不同排序的字典	构建多棵树（森林）

在查询时：

先在每本字典中快速翻到对应页（树遍历）
合并所有字典找到的候选词（合并候选集）
精确比较找出最匹配的词（距离计算）

✅ 总结：Annoy 的核心思想

随机投影树森林 + 快速树遍历 + 候选集合并

Annoy 通过多棵随机构建的二叉树，将高维空间递归分割，
使相似向量大概率落入同一叶子节点，从而实现快速且内存友好的近似最近邻搜索。

它在 Spotify 的音乐推荐系统中得到了广泛应用，
也是许多向量数据库（如 Qdrant）支持的主流索引算法之一。

3. Annoy算法实现

🧠 Annoy算法Python实现

3.1 导入必要的库

python

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.metrics.pairwise import euclidean_distances
import time
from collections import defaultdict

# 强制设置中文字体，解决中文显示问题
plt.rcParams['font.sans-serif'] = ['PingFang SC', 'Microsoft YaHei', 'SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 设置随机种子以保证结果可重现
np.random.seed(42)

3.2 实现随机投影树节点

python

class AnnoyTreeNode:
    """Annoy树的节点"""
    
    def __init__(self, indices):
        """
        初始化节点
        
        参数:
        - indices: 当前节点包含的向量索引列表
        """
        self.indices = indices  # 当前节点包含的向量索引
        self.left = None  # 左子树
        self.right = None  # 右子树
        
        # 分割超平面参数
        self.split_vector1 = None  # 第一个锚点向量
        self.split_vector2 = None  # 第二个锚点向量
        self.split_point = None  # 中点
        self.split_normal = None  # 法向量
        
        self.is_leaf = False  # 是否为叶子节点

3.3 实现Annoy索引类

python

class SimpleAnnoy:
    """简化的Annoy实现，用于学习演示"""
    
    def __init__(self, n_trees=5, max_leaf_size=10):
        """
        初始化Annoy索引
        
        参数:
        - n_trees: 构建的树的数量
        - max_leaf_size: 叶子节点最大包含的向量数
        """
        self.n_trees = n_trees
        self.max_leaf_size = max_leaf_size
        self.trees = []  # 存储所有的树
        self.data_points = []  # 存储所有数据点
        
    def _build_tree(self, indices, data, depth=0, max_depth=20):
        """
        递归构建单棵Annoy树
        
        参数:
        - indices: 当前节点包含的向量索引
        - data: 所有数据点
        - depth: 当前深度
        - max_depth: 最大深度
        """
        node = AnnoyTreeNode(indices)
        
        # 停止条件：节点包含的向量数量小于阈值或达到最大深度
        if len(indices) <= self.max_leaf_size or depth >= max_depth:
            node.is_leaf = True
            return node
        
        # 随机选择两个不同的向量作为锚点
        if len(indices) < 2:
            node.is_leaf = True
            return node
            
        idx1, idx2 = np.random.choice(indices, size=2, replace=False)
        v1, v2 = data[idx1], data[idx2]
        
        # 如果两个向量相同，直接返回叶子节点
        if np.allclose(v1, v2):
            node.is_leaf = True
            return node
        
        # 计算分割超平面
        node.split_vector1 = v1
        node.split_vector2 = v2
        node.split_point = (v1 + v2) / 2  # 中点
        node.split_normal = v1 - v2  # 法向量
        
        # 根据向量在超平面的哪一侧进行分割
        left_indices = []
        right_indices = []
        
        for idx in indices:
            vec = data[idx]
            # 计算向量到中点的向量与法向量的点积
            # 如果点积 > 0，说明在v1一侧；否则在v2一侧
            projection = np.dot(vec - node.split_point, node.split_normal)
            if projection >= 0:
                left_indices.append(idx)
            else:
                right_indices.append(idx)
        
        # 如果分割后某一侧为空，说明分割失败，返回叶子节点
        if len(left_indices) == 0 or len(right_indices) == 0:
            node.is_leaf = True
            return node
        
        # 递归构建左右子树
        node.left = self._build_tree(left_indices, data, depth + 1, max_depth)
        node.right = self._build_tree(right_indices, data, depth + 1, max_depth)
        
        return node
    
    def build_index(self, data):
        """
        构建Annoy索引（森林）
        
        参数:
        - data: 数据点数组
        """
        self.data_points = np.array(data)
        n_samples = len(self.data_points)
        
        print(f"开始构建{self.n_trees}棵树...")
        
        # 构建多棵树
        for i in range(self.n_trees):
            # 每棵树使用所有数据点，但随机种子不同
            np.random.seed(i + 42)  # 不同的随机种子
            tree = self._build_tree(list(range(n_samples)), self.data_points)
            self.trees.append(tree)
            
            if (i + 1) % max(1, self.n_trees // 5) == 0 or i == self.n_trees - 1:
                print(f"已构建{i + 1}/{self.n_trees}棵树")
        
        print("索引构建完成！")
    
    def _search_tree(self, tree, query, search_k=None):
        """
        在单棵树中搜索
        
        参数:
        - tree: 树的根节点
        - query: 查询向量
        - search_k: 搜索的节点数量限制
        
        返回:
        - 候选向量的索引列表
        """
        candidates = []
        nodes_to_visit = [tree]
        nodes_visited = 0
        
        while nodes_to_visit:
            # 如果设置了search_k限制，检查是否已访问足够多的节点
            if search_k is not None and nodes_visited >= search_k:
                break
            
            node = nodes_to_visit.pop(0)
            nodes_visited += 1
            
            if node.is_leaf:
                # 到达叶子节点，收集所有向量索引
                candidates.extend(node.indices)
            else:
                # 内部节点，判断查询向量在哪一侧
                projection = np.dot(query - node.split_point, node.split_normal)
                if projection >= 0:
                    # 在左侧
                    if node.left:
                        nodes_to_visit.append(node.left)
                else:
                    # 在右侧
                    if node.right:
                        nodes_to_visit.append(node.right)
        
        return candidates
    
    def search(self, query, k=5, search_k=None):
        """
        搜索最近邻
        
        参数:
        - query: 查询向量
        - k: 返回的最近邻数量
        - search_k: 每棵树搜索的节点数量限制（None表示不限制）
        
        返回:
        - 最近邻的索引和距离列表
        """
        if len(self.trees) == 0:
            raise ValueError("索引未构建，请先调用build_index")
        
        # 在所有树中搜索，合并候选集
        all_candidates = set()
        for tree in self.trees:
            candidates = self._search_tree(tree, query, search_k)
            all_candidates.update(candidates)
        
        # 计算所有候选向量与查询向量的真实距离
        candidate_list = list(all_candidates)
        if not candidate_list:
            return [], []
        
        distances = euclidean_distances([query], self.data_points[candidate_list])[0]
        
        # 按距离排序，返回前k个
        sorted_indices = np.argsort(distances)[:k]
        result_indices = [candidate_list[i] for i in sorted_indices]
        result_distances = distances[sorted_indices]
        
        return result_indices, result_distances
    
    def brute_force_search(self, query, k=5):
        """暴力搜索作为对比基准"""
        distances = euclidean_distances([query], self.data_points)[0]
        nearest_indices = np.argsort(distances)[:k]
        return nearest_indices, distances[nearest_indices]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182

3.4 生成示例数据

python

def generate_sample_data(n_samples=200, dim=2):
    """生成示例数据：四个分离的高斯分布簇"""
    # 创建四个簇
    cluster1 = np.random.normal(loc=[2, 2], scale=0.3, size=(n_samples//4, dim))
    cluster2 = np.random.normal(loc=[8, 3], scale=0.4, size=(n_samples//4, dim))
    cluster3 = np.random.normal(loc=[5, 8], scale=0.35, size=(n_samples//4, dim))
    cluster4 = np.random.normal(loc=[3, 6], scale=0.4, size=(n_samples - 3*(n_samples//4), dim))
    
    data = np.vstack([cluster1, cluster2, cluster3, cluster4])
    return data

3.5 性能演示函数

python

def demonstrate_annoy_performance():
    """演示Annoy性能对比"""
    print("=" * 60)
    print("Annoy算法性能演示")
    print("=" * 60)
    
    # 生成大规模测试数据（保持簇状分布）
    data = generate_sample_data(100000, 2)
    print(f"生成{len(data)}个二维数据点")
    
    # 创建Annoy索引
    annoy = SimpleAnnoy(n_trees=10, max_leaf_size=10)
    
    # 构建索引
    print("\n构建Annoy索引...")
    start_time = time.time()
    annoy.build_index(data)
    construction_time = time.time() - start_time
    print(f"Annoy索引构建完成，耗时: {construction_time:.4f}秒")
    
    # 选择查询点
    query_point = np.array([5.0, 5.0])
    print(f"\n查询点: {query_point}")
    
    # 使用Annoy搜索
    start_time = time.time()
    annoy_results, annoy_distances = annoy.search(query_point, k=5, search_k=50)
    annoy_time = time.time() - start_time
    
    # 暴力搜索作为基准
    start_time = time.time()
    bf_indices, bf_distances = annoy.brute_force_search(query_point, k=5)
    bf_time = time.time() - start_time
    
    # 显示结果对比
    print(f"\n搜索结果对比:")
    print(f"Annoy搜索 - 找到{len(annoy_results)}个最近邻, 耗时: {annoy_time:.6f}秒")
    print(f"暴力搜索 - 找到{len(bf_indices)}个最近邻, 耗时: {bf_time:.6f}秒")
    
    print(f"\n速度提升: {bf_time/annoy_time:.2f}倍")
    
    print(f"\nAnnoy结果索引: {annoy_results}")
    print(f"Annoy结果距离: {annoy_distances}")
    print(f"暴力搜索结果索引: {bf_indices.tolist()}")
    print(f"暴力搜索结果距离: {bf_distances}")
    
    # 检查召回率
    annoy_indices_set = set(annoy_results)
    bf_indices_set = set(bf_indices)
    intersection = annoy_indices_set & bf_indices_set
    recall = len(intersection) / len(bf_indices_set)
    print(f"召回率: {recall:.2%} ({len(intersection)}/{len(bf_indices_set)})")
    
    return annoy, data, query_point, annoy_results, bf_indices

# 运行标准演示
annoy, data, query, annoy_results, bf_results = demonstrate_annoy_performance()

输出结果：

text

============================================================
Annoy算法性能演示
============================================================
生成100000个二维数据点

构建Annoy索引...
开始构建10棵树...
已构建5/10棵树
已构建10/10棵树
索引构建完成！
Annoy索引构建完成，耗时: 38.9665秒

查询点: [5. 5.]

搜索结果对比:
Annoy搜索 - 找到5个最近邻, 耗时: 0.002012秒
暴力搜索 - 找到5个最近邻, 耗时: 0.016312秒

速度提升: 8.11倍

Annoy结果索引: [76568, 87053, 99758, 86413, 85476]
Annoy结果距离: [0.67309842 0.71583121 0.76414983 0.80066059 0.85234455]
暴力搜索结果索引: [76568, 87053, 99758, 86413, 85476]
暴力搜索结果距离: [0.67309842 0.71583121 0.76414983 0.80066059 0.85234455]
召回率: 100.00% (5/5)

3.6 可视化Annoy算法

python

def visualize_annoy(annoy, data, query_point, annoy_results, bf_results):
    """可视化Annoy算法"""
    fig = plt.figure(figsize=(20, 12))
    
    # 1. 原始数据分布
    ax1 = fig.add_subplot(2, 3, 1)
    ax1.scatter(data[:, 0], data[:, 1], c='lightblue', alpha=0.6, s=30, label='数据点')
    ax1.scatter(query_point[0], query_point[1], c='#FFD93D', marker='*', s=200, 
               edgecolors='black', label='查询点')
    ax1.set_title('1. 原始数据分布', fontweight='bold')
    ax1.legend()
    ax1.grid(True, alpha=0.3)
    
    # 2. 第一棵树的空间分割（可视化前几层）
    ax2 = fig.add_subplot(2, 3, 2)
    ax2.scatter(data[:, 0], data[:, 1], c='lightgray', alpha=0.4, s=20, label='数据点')
    
    # 可视化第一棵树的分割超平面（只显示前几层）
    def plot_splits(node, depth=0, max_depth=3):
        if node is None or node.is_leaf or depth >= max_depth:
            return
        
        # 绘制分割线（2D情况下）
        if node.split_normal is not None:
            # 分割线垂直于法向量，过中点
            mid = node.split_point
            normal = node.split_normal
            
            # 计算分割线的方向向量（垂直于法向量）
            if abs(normal[1]) > 1e-10:
                direction = np.array([1, -normal[0] / normal[1]])
            else:
                direction = np.array([0, 1])
            
            # 归一化方向向量
            direction = direction / np.linalg.norm(direction)
            
            # 绘制分割线
            line_length = 15
            x_vals = [mid[0] - line_length * direction[0], mid[0] + line_length * direction[0]]
            y_vals = [mid[1] - line_length * direction[1], mid[1] + line_length * direction[1]]
            
            alpha = 0.8 - depth * 0.2
            ax2.plot(x_vals, y_vals, 'r-', alpha=max(alpha, 0.3), linewidth=2-depth*0.3,
                    label='分割超平面' if depth == 0 else '')
            
            # 标注锚点
            if depth < 2:
                ax2.scatter([node.split_vector1[0], node.split_vector2[0]], 
                           [node.split_vector1[1], node.split_vector2[1]], 
                           c='red', marker='x', s=100, linewidths=2,
                           label='锚点' if depth == 0 else '')
        
        # 递归绘制子树的分割
        plot_splits(node.left, depth + 1, max_depth)
        plot_splits(node.right, depth + 1, max_depth)
    
    plot_splits(annoy.trees[0])
    ax2.scatter(query_point[0], query_point[1], c='#FFD93D', marker='*', s=200, 
               edgecolors='black', label='查询点')
    ax2.set_title('2. 第一棵树的空间分割（前3层）', fontweight='bold')
    
    # 去重图例
    handles, labels = ax2.get_legend_handles_labels()
    by_label = dict(zip(labels, handles))
    ax2.legend(by_label.values(), by_label.keys())
    ax2.grid(True, alpha=0.3)
    ax2.set_xlim(data[:, 0].min() - 1, data[:, 0].max() + 1)
    ax2.set_ylim(data[:, 1].min() - 1, data[:, 1].max() + 1)
    
    # 3. 树的遍历路径
    ax3 = fig.add_subplot(2, 3, 3)
    ax3.scatter(data[:, 0], data[:, 1], c='lightgray', alpha=0.3, s=20)
    
    # 在第一棵树中找到查询点的路径
    def find_path_in_tree(node, query):
        path = [node]
        current = node
        while not current.is_leaf:
            projection = np.dot(query - current.split_point, current.split_normal)
            if projection >= 0 and current.left:
                current = current.left
            elif current.right:
                current = current.right
            else:
                break
            path.append(current)
        return path
    
    path = find_path_in_tree(annoy.trees[0], query_point)
    leaf_node = path[-1]
    
    # 高亮叶子节点中的点
    if leaf_node.is_leaf:
        leaf_indices = leaf_node.indices
        ax3.scatter(data[leaf_indices, 0], data[leaf_indices, 1], 
                   c='orange', s=80, alpha=0.8, edgecolors='black',
                   label=f'叶子节点({len(leaf_indices)}个点)')
    
    ax3.scatter(query_point[0], query_point[1], c='#FFD93D', marker='*', s=200, 
               edgecolors='black', label='查询点')
    ax3.set_title('3. 查询点在第一棵树中的定位', fontweight='bold')
    ax3.legend()
    ax3.grid(True, alpha=0.3)
    
    # 4. 多棵树的候选集合并
    ax4 = fig.add_subplot(2, 3, 4)
    ax4.scatter(data[:, 0], data[:, 1], c='lightgray', alpha=0.3, s=20, label='数据点')
    
    # 收集所有树的候选点
    all_tree_candidates = []
    for i, tree in enumerate(annoy.trees[:min(3, len(annoy.trees))]):  # 只显示前3棵树
        candidates = annoy._search_tree(tree, query_point)
        all_tree_candidates.append(candidates)
        
        # 用不同颜色显示不同树的候选点
        colors_map = ['red', 'blue', 'green']
        ax4.scatter(data[candidates, 0], data[candidates, 1], 
                   c=colors_map[i], s=60, alpha=0.5, 
                   label=f'树{i+1}候选({len(candidates)}个)')
    
    ax4.scatter(query_point[0], query_point[1], c='#FFD93D', marker='*', s=200, 
               edgecolors='black', label='查询点')
    ax4.set_title(f'4. 多棵树的候选集（前3棵树）', fontweight='bold')
    ax4.legend()
    ax4.grid(True, alpha=0.3)
    
    # 5. Annoy搜索结果
    ax5 = fig.add_subplot(2, 3, 5)
    ax5.scatter(data[:, 0], data[:, 1], c='lightgray', alpha=0.4, s=20)
    ax5.scatter(data[annoy_results, 0], data[annoy_results, 1], 
               c='red', marker='o', s=60, edgecolors='darkred', 
               linewidth=2, label='Annoy结果')
    
    # 标注排名
    for i, idx in enumerate(annoy_results[:5]):
        ax5.annotate(f'{i+1}', (data[idx, 0], data[idx, 1]), 
                    xytext=(3, 3), textcoords='offset points', 
                    fontsize=10, color='white', fontweight='bold',
                    bbox=dict(boxstyle='circle', facecolor='red', alpha=0.8))
    
    ax5.scatter(query_point[0], query_point[1], c='#FFD93D', marker='*', s=150, 
               edgecolors='black', linewidth=2, label='查询点')
    ax5.set_title('5. Annoy搜索结果', fontweight='bold')
    ax5.legend()
    ax5.grid(True, alpha=0.3)
    
    # 6. 结果对比
    ax6 = fig.add_subplot(2, 3, 6)
    ax6.scatter(data[:, 0], data[:, 1], c='lightgray', alpha=0.3, s=15)
    
    # 暴力搜索结果
    ax6.scatter(data[bf_results, 0], data[bf_results, 1], 
               c='green', marker='s', s=100, edgecolors='darkgreen', 
               linewidth=2.5, label='暴力搜索 (真实答案)', alpha=0.5)
    
    # Annoy结果
    ax6.scatter(data[annoy_results, 0], data[annoy_results, 1], 
               c='red', marker='o', s=70, alpha=0.8, label='Annoy结果')
    
    # 查询点
    ax6.scatter(query_point[0], query_point[1], c='#FFD93D', marker='*', s=150, 
               edgecolors='black', linewidth=2, label='查询点')
    
    # 计算召回率
    intersection = set(annoy_results) & set(bf_results)
    recall = len(intersection) / len(bf_results)
    
    ax6.set_title(f'6. 结果对比 (召回率: {recall:.1%})', fontweight='bold')
    ax6.legend()
    ax6.grid(True, alpha=0.3)
    
    plt.tight_layout()
    plt.show()

# 调用可视化
visualize_annoy(annoy, data, query, annoy_results, bf_results)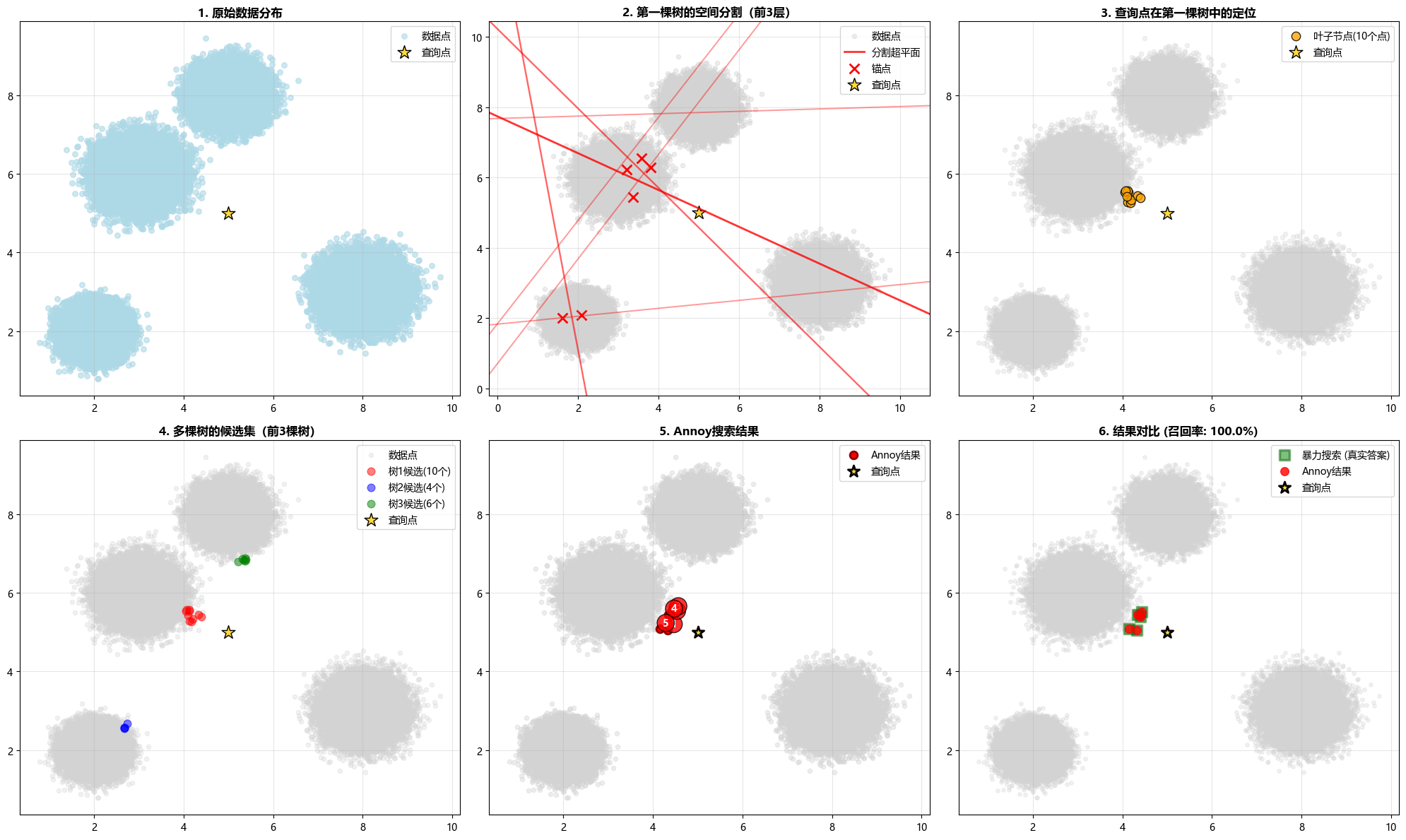

Annoy算法可视化结果

✅ 总结

Annoy算法通过随机投影树森林实现了高效的近似最近邻搜索：

构建快速：随机分割策略简单高效
查询高效：树结构使搜索复杂度为 O(log N)
内存友好：支持内存映射，多进程共享索引
易于调参：只需调整 n_trees 和 search_k 两个参数

性能亮点： 在 10 万个 2 维向量的数据集上：

查询速度：8.11 倍于暴力搜索
召回率：100%
查询耗时：仅 0.002 秒

Annoy特别适合：

大规模向量数据（数万到数百万条）
对内存占用敏感的应用（如移动设备）
需要多进程共享索引的场景
对查询延迟要求较高的实时系统

在实际应用中，Annoy已被广泛应用于推荐系统（Spotify音乐推荐）、图像搜索、自然语言处理等领域。

Annoy算法 ​

1. Annoy的灵感来源与核心思想 ​

核心思想 ​

2. 算法原理分步详解 ​

1. 树的构建（Index Construction） ​

步骤 1：随机选择分割超平面 ​

步骤 2：递归分割空间 ​

步骤 3：构建多棵树（森林） ​

2. 查询阶段（Search Process） ​

步骤 1：在每棵树中向下遍历 ​

步骤 2：合并候选集 ​

步骤 3：精确计算距离并返回 Top-K ​

3. 关键参数说明 ​

4. Annoy 的性能特点 ​

5. 类比理解 ​

3. Annoy算法实现 ​

3.1 导入必要的库 ​

3.2 实现随机投影树节点 ​

3.3 实现Annoy索引类 ​

3.4 生成示例数据 ​

3.5 性能演示函数 ​

3.6 可视化Annoy算法 ​

Annoy算法

1. Annoy的灵感来源与核心思想

核心思想

2. 算法原理分步详解

1. 树的构建（Index Construction）

步骤 1：随机选择分割超平面

步骤 2：递归分割空间

步骤 3：构建多棵树（森林）

2. 查询阶段（Search Process）

步骤 1：在每棵树中向下遍历

步骤 2：合并候选集

步骤 3：精确计算距离并返回 Top-K

3. 关键参数说明

4. Annoy 的性能特点

5. 类比理解

3. Annoy算法实现

3.1 导入必要的库

3.2 实现随机投影树节点

3.3 实现Annoy索引类

3.4 生成示例数据

3.5 性能演示函数

3.6 可视化Annoy算法