第3章 k近邻法
习题3.1
参照图3.1,在二维空间中给出实例点,画出
解答:
解答思路:
- 参照图3.1,使用已给的实例点,采用sklearn的KNeighborsClassifier分类器,对k=1和2时的模型进行训练
- 使用matplotlib的contourf和scatter,画出k为1和2时的k近邻法构成的空间划分
- 根据模型得到的预测结果,计算预测准确率,并设置图形标题
- 根据程序生成的图,比较k为1和2时,k值选择与模型复杂度、预测准确率的关系
解答步骤:
第1、2、3步:使用已给的实例点,对
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
%matplotlib inline
data = np.array([[5, 12, 1],
[6, 21, 0],
[14, 5, 0],
[16, 10, 0],
[13, 19, 0],
[13, 32, 1],
[17, 27, 1],
[18, 24, 1],
[20, 20, 0],
[23, 14, 1],
[23, 25, 1],
[23, 31, 1],
[26, 8, 0],
[30, 17, 1],
[30, 26, 1],
[34, 8, 0],
[34, 19, 1],
[37, 28, 1]])
# 得到特征向量
X_train = data[:, 0:2]
# 得到类别向量
y_train = data[:, 2]
#(1)使用已给的实例点,采用sklearn的KNeighborsClassifier分类器,
# 对k=1和2时的模型进行训练
# 分别构造k=1和k=2的k近邻模型
models = (KNeighborsClassifier(n_neighbors=1, n_jobs=-1),
KNeighborsClassifier(n_neighbors=2, n_jobs=-1))
# 模型训练
models = (clf.fit(X_train, y_train) for clf in models)# 设置图形标题
titles = ('K Neighbors with k=1',
'K Neighbors with k=2')
# 设置图形的大小和图间距
fig = plt.figure(figsize=(15, 5))
plt.subplots_adjust(wspace=0.4, hspace=0.4)
# 分别获取第1个和第2个特征向量
X0, X1 = X_train[:, 0], X_train[:, 1]
# 得到坐标轴的最小值和最大值
x_min, x_max = X0.min() - 1, X0.max() + 1
y_min, y_max = X1.min() - 1, X1.max() + 1
# 构造网格点坐标矩阵
# 设置0.2的目的是生成更多的网格点,数值越小,划分空间之间的分隔线越清晰
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.2),
np.arange(y_min, y_max, 0.2))
for clf, title, ax in zip(models, titles, fig.subplots(1, 2).flatten()):
# (2)使用matplotlib的contourf和scatter,画出k为1和2时的k近邻法构成的空间划分
# 对所有网格点进行预测
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 设置颜色列表
colors = ('red', 'green', 'lightgreen', 'gray', 'cyan')
# 根据类别数生成颜色
cmap = ListedColormap(colors[:len(np.unique(Z))])
# 绘制分隔线,contourf函数用于绘制等高线,alpha表示颜色的透明度,一般设置成0.5
ax.contourf(xx, yy, Z, cmap=cmap, alpha=0.5)
# 绘制样本点
ax.scatter(X0, X1, c=y_train, s=50, edgecolors='k', cmap=cmap, alpha=0.5)
# (3)根据模型得到的预测结果,计算预测准确率,并设置图形标题
# 计算预测准确率
acc = clf.score(X_train, y_train)
# 设置标题
ax.set_title(title + ' (Accuracy: %d%%)' % (acc * 100))
plt.show()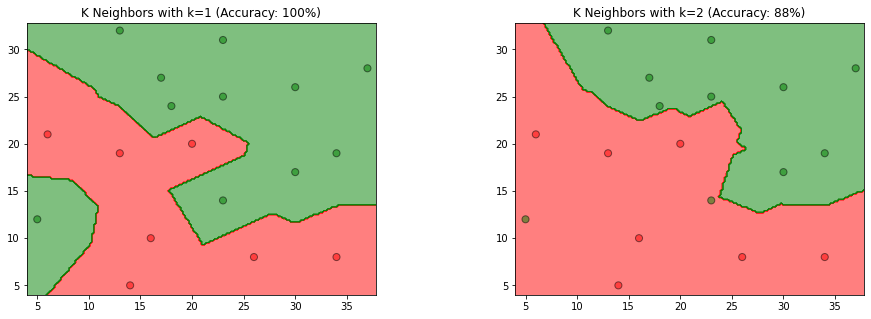
补充知识:
np.meshgrid方法:用于构造网格点坐标矩阵,可参考https://blog.csdn.net/lllxxq141592654/article/details/81532855
第4步:比较
值选择与模型复杂度的关系
根据书中第3.2.3节值的选择:
如果选择较小的
值,就相当于用较小的邻域中的训练实例进行预测,“学习”的近似误差会减小,只有与输入实例较近的(相似的)训练实例才会对预测结果起作用。 值的减小就意味着整体模型变得复杂,容易发生过拟合。
如果选择较大的值,就相当于用较大邻域中的训练实例进行预测。 值的增大就意味着整体的模型变得简单。
综上所属,
值选择与预测准确率的关系
从图中观察到,当时,模型易产生过拟合,当 时准确率仅有88%,故在过拟合发生前, 值越大,预测准确率越低,也反映模型泛化能力越差,模型简单。反之, 值越小,预测准确率越高,模型具有更好的泛化能力,模型复杂。
习题3.2
利用例题3.2构造的
解答:
解答思路:
方法一:
- 使用sklearn的KDTree类,结合例题3.2构建平衡
树,配置相关参数(构建平衡树kd树算法,见书中第54页算法3.2内容); - 使用tree.query方法,查找(3, 4.5)的最近邻点(搜索kd树算法,见书中第55页第3.3.2节内容);
- 根据第3步返回的参数,得到最近邻点。
方法二:
根据书中第3章的算法3.3用
解答步骤:
方法一:
import numpy as np
from sklearn.neighbors import KDTree
# 构造例题3.2的数据集
train_data = np.array([[2, 3],
[5, 4],
[9, 6],
[4, 7],
[8, 1],
[7, 2]])
# (1)使用sklearn的KDTree类,构建平衡kd树
# 设置leaf_size为2,表示平衡树
tree = KDTree(train_data, leaf_size=2)
# (2)使用tree.query方法,设置k=1,查找(3, 4.5)的最近邻点
# dist表示与最近邻点的距离,ind表示最近邻点在train_data的位置
dist, ind = tree.query(np.array([[3, 4.5]]), k=1)
node_index = ind[0]
# (3)得到最近邻点
x1 = train_data[node_index][0][0]
x2 = train_data[node_index][0][1]
print("x点(3,4.5)的最近邻点是({0}, {1})".format(x1, x2))x点(3,4.5)的最近邻点是(2, 3)
可得到点
方法二:
- 首先找到点
所在领域的叶节点 ,则最近邻点一定在以 为圆心, 到 距离为半径的圆内; - 找到
的父节点 , 的另一子节点为 ,此时 在圆内,故 为最新的最近邻点,并形成以 为圆心,以 到 距离为半径的圆; - 继续探索
的父节点 , 的另一个子节点 对应的区域不与圆相交,故不存在最近邻点,所以最近邻点为 。
可得到点
习题3.3
参照算法3.3,写出输出为
解答:
解答思路:
- 参考书中第3章的算法3.3(用
树的最近邻搜索),写出输出为 的 近邻算法; - 根据算法步骤,写出算法代码,并用习题3.2的解进行验证。
解答步骤:
第1步:用
根据书中第3章算法3.3:
算法3.3 用
树的最近邻搜索
输出:的k近邻
(1)在树中找出包含目标点 的叶结点:从根结点出发,递归地向下访问树。若目标点 当前维的坐标小于切分点的坐标,则移动到左子结点,否则移动到右子结点,直到子结点为叶结点为止;
(2)如果“当前近邻点集”元素数量小于 或者叶节点距离小于“当前 近邻点集”中最远点距离,那么将叶节点插入“当前k近邻点集”;
(3)递归地向上回退,在每个结点进行以下操作:
(a)如果“当前近邻点集”元素数量小于 或者当前节点距离小于“当前 近邻点集”中最远点距离,那么将该节点插入“当前 近邻点集”。
(b)检查另一子结点对应的区域是否与以目标点为球心、以目标点与“当前近邻点集”中最远点间的距离为半径的超球体相交。
如果相交,可能在另一个子结点对应的区域内存在距目标点更近的点,移动到另一个子结点,接着,递归地进行近邻搜索;
如果不相交,向上回退;
(4)当回退到根结点时,搜索结束,最后的“当前近邻点集”即为 的近邻点。
第2步:根据算法步骤,写出算法代码,并用习题3.2的解进行验证
import json
class Node:
"""节点类"""
def __init__(self, value, index, left_child, right_child):
self.value = value.tolist()
self.index = index
self.left_child = left_child
self.right_child = right_child
def __repr__(self):
return json.dumps(self, indent=3, default=lambda obj: obj.__dict__, ensure_ascii=False, allow_nan=False)class KDTree:
"""kd tree类"""
def __init__(self, data):
# 数据集
self.data = np.asarray(data)
# kd树
self.kd_tree = None
# 创建平衡kd树
self._create_kd_tree(data)
def _split_sub_tree(self, data, depth=0):
# 算法3.2第3步:直到子区域没有实例存在时停止
if len(data) == 0:
return None
# 算法3.2第2步:选择切分坐标轴, 从0开始(书中是从1开始)
l = depth % data.shape[1]
# 对数据进行排序
data = data[data[:, l].argsort()]
# 算法3.2第1步:将所有实例坐标的中位数作为切分点
median_index = data.shape[0] // 2
# 获取结点在数据集中的位置
node_index = [i for i, v in enumerate(
self.data) if list(v) == list(data[median_index])]
return Node(
# 本结点
value=data[median_index],
# 本结点在数据集中的位置
index=node_index[0],
# 左子结点
left_child=self._split_sub_tree(data[:median_index], depth + 1),
# 右子结点
right_child=self._split_sub_tree(
data[median_index + 1:], depth + 1)
)
def _create_kd_tree(self, X):
self.kd_tree = self._split_sub_tree(X)
def query(self, data, k=1):
data = np.asarray(data)
hits = self._search(data, self.kd_tree, k=k, k_neighbors_sets=list())
dd = np.array([hit[0] for hit in hits])
ii = np.array([hit[1] for hit in hits])
return dd, ii
def __repr__(self):
return str(self.kd_tree)
@staticmethod
def _cal_node_distance(node1, node2):
"""计算两个结点之间的距离"""
return np.sqrt(np.sum(np.square(node1 - node2)))
def _search(self, point, tree=None, k=1, k_neighbors_sets=None, depth=0):
n = point.shape[1]
if k_neighbors_sets is None:
k_neighbors_sets = []
if tree is None:
return k_neighbors_sets
# (1)找到包含目标点x的叶节点
if tree.left_child is None and tree.right_child is None:
# 更新当前k近邻集
return self._update_k_neighbor_sets(k_neighbors_sets, k, tree, point)
# 递归地向下访问kd树
if point[0][depth % n] < tree.value[depth % n]:
direct = 'left'
next_branch = tree.left_child
else:
direct = 'right'
next_branch = tree.right_child
if next_branch is not None:
# (3)(b)检查另一子节点对应的区域是否相交
k_neighbors_sets = self._search(point, tree=next_branch, k=k, depth=depth + 1,
k_neighbors_sets=k_neighbors_sets)
# 计算目标点与切分点形成的分割超平面的距离
temp_dist = abs(tree.value[depth % n] - point[0][depth % n])
# 判断超球体是否与超平面相交
if not (k_neighbors_sets[0][0] < temp_dist and len(k_neighbors_sets) == k): # 换到另一侧
# 如果相交,递归地进行近邻搜索
# (3)(a)判断当前结点,并更新当前k近邻点集
k_neighbors_sets = self._update_k_neighbor_sets(k_neighbors_sets, k, tree, point) # tree 返回父节点
if direct == 'left':
return self._search(point, tree=tree.right_child, k=k, depth=depth + 1,
k_neighbors_sets=k_neighbors_sets)
else:
return self._search(point, tree=tree.left_child, k=k, depth=depth + 1,
k_neighbors_sets=k_neighbors_sets)
else:
# 如果选定的子树为空,则直接判断是否需要回溯另一侧子树
# 如果 k 近邻集合未满,则需要回溯另一侧子树
if len(k_neighbors_sets) < k:
# 如果相交,递归地进行近邻搜索
# (3)(a)判断当前结点,并更新当前k近邻点集
k_neighbors_sets = self._update_k_neighbor_sets(k_neighbors_sets, k, tree, point) # tree 返回父节点
if direct == 'left':
return self._search(point, tree=tree.right_child, k=k, depth=depth + 1,
k_neighbors_sets=k_neighbors_sets)
else:
return self._search(point, tree=tree.left_child, k=k, depth=depth + 1,
k_neighbors_sets=k_neighbors_sets)
return k_neighbors_sets
def _update_k_neighbor_sets(self, best, k, tree, point):
# 计算目标点与当前结点的距离
node_distance = self._cal_node_distance(point, tree.value)
if len(best) == 0:
best.append((node_distance, tree.index, tree.value))
elif len(best) < k:
# 如果“当前k近邻点集”元素数量小于k
self._insert_k_neighbor_sets(best, tree, node_distance)
else:
# 叶节点距离小于“当前 𝑘 近邻点集”中最远点距离
if best[0][0] > node_distance:
best = best[1:]
self._insert_k_neighbor_sets(best, tree, node_distance)
return best
@staticmethod
def _insert_k_neighbor_sets(best, tree, node_distance):
"""将距离最远的结点排在前面"""
n = len(best)
for i, item in enumerate(best):
if item[0] < node_distance:
# 将距离最远的结点插入到前面
best.insert(i, (node_distance, tree.index, tree.value))
break
if len(best) == n:
best.append((node_distance, tree.index, tree.value))# 打印信息
def print_k_neighbor_sets(k, ii, dd):
if k == 1:
text = "x点的最近邻点是"
else:
text = "x点的%d个近邻点是" % k
for i, index in enumerate(ii):
res = X_train[index]
if i == 0:
text += str(tuple(res))
else:
text += ", " + str(tuple(res))
if k == 1:
text += ",距离是"
else:
text += ",距离分别是"
for i, dist in enumerate(dd):
if i == 0:
text += "%.4f" % dist
else:
text += ", %.4f" % dist
print(text)import numpy as np
X_train = np.array([[2, 3],
[5, 4],
[9, 6],
[4, 7],
[8, 1],
[7, 2]])
kd_tree = KDTree(X_train)
# 设置k值
k = 1
# 查找邻近的结点
dists, indices = kd_tree.query(np.array([[3, 4.5]]), k=k)
# 打印邻近结点
print_k_neighbor_sets(k, indices, dists)x点的最近邻点是(2, 3),距离是1.8028
# 打印kd树
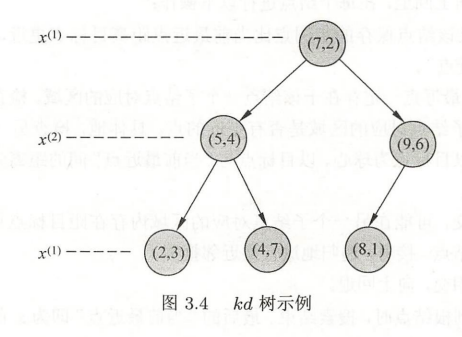
kd_tree{
"value": [
7,
2
],
"index": 5,
"left_child": {
"value": [
5,
4
],
"index": 1,
"left_child": {
"value": [
2,
3
],
"index": 0,
"left_child": null,
"right_child": null
},
"right_child": {
"value": [
4,
7
],
"index": 3,
"left_child": null,
"right_child": null
}
},
"right_child": {
"value": [
9,
6
],
"index": 2,
"left_child": {
"value": [
8,
1
],
"index": 4,
"left_child": null,
"right_child": null
},
"right_child": null
}
}
上述打印的平衡kd树和书中第55页的图3.4 kd树示例一致。
更换数据集,使用更高维度的数据,并设置
import numpy as np
X_train = np.array([[2, 3, 4],
[5, 4, 4],
[9, 6, 4],
[4, 7, 4],
[8, 1, 4],
[7, 2, 4]])
kd_tree = KDTree(X_train)
# 设置k值
k = 3
# 查找邻近的结点
dists, indices = kd_tree.query(np.array([[3, 4.5, 4]]), k=k)
# 打印邻近结点
print_k_neighbor_sets(k, indices, dists)x点的3个近邻点是(4, 7, 4), (5, 4, 4), (2, 3, 4),距离分别是2.6926, 2.0616, 1.8028
