第9章 EM算法及其推广

习题9.1

  如例9.1的三硬币模型，假设观测数据不变，试选择不同的初值，例如，${\pi }^{(0)}=0.46,p^{(0)}=0.55,q^{(0)}=0.67$，求模型参数为$\theta =(\pi ,p,q)$的极大似然估计。

解答：

解答思路：

1. 列出例9.1的三硬币模型；
2. 写出三硬币模型的EM算法；
3. 根据上述EM算法，编写代码，并求出模型参数的极大似然估计。

解答步骤：

第1步：例9.1的三硬币模型

  根据书中第9章的例9.1（三硬币模型）：

  例9.1（三硬币模型） 假设有3枚硬币，分别记作A，B，C。这些硬币正面出现的概率分别是$\pi$，$p$和$q$。进行如下掷硬币试验：先掷硬币A，根据其结果选出硬币B或硬币C，正面选硬币B，反面选硬币C；然后掷选出的硬币，掷硬币的结果，出现正面记作1，出现方面记作0；独立地重复$n$次试验（这里，$n=10$），观测结果如下：

$$1,1,0,1,0,0,1,0,1,1$$

假设只能观测到掷硬币的结果，不能观测掷硬币的过程。

  三硬币模型可以写作

$$\begin{array}{rl}P(y|\theta )& =\sum _{z}P(y,z|\theta )=\sum _{z}P(z|\theta )P(y|z,\theta )\\ & =\pi p^y(1-p{)}^{1-y}+(1-\pi )q^y(1-q{)}^{1-y}\end{array}$$

这里：

1. 随机变量$y$是观测变量，表示一次试验观测的结果是1或0；
2. 随机变量$z$是隐变量，表示未观测到的掷硬币A的结果；
3. $\theta =(\pi ,p,q)$是模型参数。

第2步：三硬币模型的EM算法

  根据书中第9章的例9.1的三硬币模型的EM算法：

  EM算法首先选取参数的初值，记作${\theta }^{(0)}=({\pi }^{(0)},p^{(0)},q^{(0)})$，然后通过下面的步骤迭代计算参数的估计值，直至收敛为止。第$i$次迭代参数的估计值为${\theta }^{(i)}=({\pi }^{(i)},p^{(i)},q^{(i)})$。EM算法的第$i+1$次迭代如下：

  E步：计算在模型参数${\pi }^{(i)},p^{(i)},q^{(i)}$下观测数据$y_j$来自掷硬币B的概率

$${\mu }_j^{(i+1)}=\frac{{\pi }^{(i)}(p^{(i)}{)}^{y_j}(1-p^{(i)}{)}^{1-y_j}}{{\pi }^{(i)}(p^{(i)}{)}^{y_j}(1-p^{(i)}{)}^{1-y_j}+(1-{\pi }^{(i)})(q^{(i)}{)}^{y_j}(1-q^{(i)}{)}^{1-y_j}}$$

  M步：计算模型参数的新估计值

$$\begin{gathered} {\pi }^{(i+1)}=\frac{1}{n}\sum _{j=1}^N{\mu }_j^{(i+1)} \\ {p}^{(i+1)}=\frac{{\displaystyle \sum _{j=1}^n{\mu }_j^{(i+1)}{y}_j}}{{\displaystyle \sum _{j=1}^n{\mu }_j^{(i+1)}}} \\ {q}^{(i+1)}=\frac{{\displaystyle \sum _{j=1}^n(1-{\mu }_j^{(i+1)})y_j}}{{\displaystyle \sum _{j=1}^n(1-{\mu }_j^{(i+1)})}} \end{gathered}$$

第3步：编写代码并求出模型参数的极大似然估计

import math


class ThreeCoinEM:
    def __init__(self, prob, tol=1e-6, max_iter=1000):
        """
        初始化模型参数
        :param prob: 模型参数的初值
        :param tol: 收敛阈值
        :param max_iter: 最大迭代次数
        """
        self.prob_A, self.prob_B, self.prob_C = prob
        self.tol = tol
        self.max_iter = max_iter

    def calc_mu(self, j):
        """
        （E步）计算mu
        :param j: 观测数据y的第j个
        :return: 在模型参数下观测数据yj来自掷硬币B的概率
        """
        # 掷硬币A观测结果为正面
        pro_1 = self.prob_A * \
            math.pow(self.prob_B, data[j]) * \
            math.pow((1 - self.prob_B), 1 - data[j])
        # 掷硬币A观测结果为反面
        pro_2 = (1 - self.prob_A) * math.pow(self.prob_C,
                                             data[j]) * math.pow((1 - self.prob_C), 1 - data[j])
        return pro_1 / (pro_1 + pro_2)

    def fit(self, data):
        count = len(data)
        print("模型参数的初值：")
        print("prob_A={}, prob_B={}, prob_C={}".format(
            self.prob_A, self.prob_B, self.prob_C))
        print("EM算法训练过程：")
        for i in range(self.max_iter):
            # （E步）得到在模型参数下观测数据yj来自掷硬币B的概率
            _mu = [self.calc_mu(j) for j in range(count)]
            # （M步）计算模型参数的新估计值
            prob_A = 1 / count * sum(_mu)
            prob_B = sum([_mu[k] * data[k] for k in range(count)]) \
                / sum([_mu[k] for k in range(count)])
            prob_C = sum([(1 - _mu[k]) * data[k] for k in range(count)]) \
                / sum([(1 - _mu[k]) for k in range(count)])
            print('第{}次：prob_A={:.4f}, prob_B={:.4f}, prob_C={:.4f}'.format(
                i + 1, prob_A, prob_B, prob_C))
            # 计算误差值
            error = abs(self.prob_A - prob_A) + \
                abs(self.prob_B - prob_B) + abs(self.prob_C - prob_C)
            self.prob_A = prob_A
            self.prob_B = prob_B
            self.prob_C = prob_C
            # 判断是否收敛
            if error < self.tol:
                print("模型参数的极大似然估计：")
                print("prob_A={:.4f}, prob_B={:.4f}, prob_C={:.4f}".format(self.prob_A, self.prob_B,
                                                                           self.prob_C))
                break

# 加载数据
data = [1, 1, 0, 1, 0, 0, 1, 0, 1, 1]
# 模型参数的初值
init_prob = [0.46, 0.55, 0.67]

# 三硬币模型的EM模型
em = ThreeCoinEM(prob=init_prob, tol=1e-5, max_iter=100)
# 模型训练
em.fit(data)

模型参数的初值：
prob_A=0.46, prob_B=0.55, prob_C=0.67
EM算法训练过程：
第1次：prob_A=0.4619, prob_B=0.5346, prob_C=0.6561
第2次：prob_A=0.4619, prob_B=0.5346, prob_C=0.6561
模型参数的极大似然估计：
prob_A=0.4619, prob_B=0.5346, prob_C=0.6561

  可见通过两次迭代，模型参数已经收敛，三硬币正面出现的概率分别为0.4619，0.5346，0.6561

习题9.2

证明引理9.2。

解答：

解答思路：

1. 写出需要证明的引理9.2；
2. 列出$F$函数定义；
3. 根据引理9.1，进行公式推导；
4. 根据约束条件${\displaystyle \sum _z{\tilde{P}}_{\theta }(Z)=1}$，可证明引理9.2。

解答步骤：

第1步：需要证明的引理9.2

  根据书中第9.4.1节的引理9.2：

  引理9.2 若${\tilde{P}}_{\theta }(Z)=P(Z|Y,\theta )$，则

$$\begin{array}{}\text{(9.36)}& F(\tilde{P},\theta )=\log P(Y|\theta )\end{array}$$

第2步：$F$函数定义

  根据书中第9章的定义9.3的$F$函数定义：

  定义9.3（$F$函数） 假设隐变量数据$Z$的概率分布为$\tilde{P}(Z)$，定义分布$\tilde{P}$与参数$\theta$的函数$F(\tilde{P},\theta )$如下：

$$\begin{array}{}\text{(9.33)}& F(\tilde{P},\theta )=E_{\tilde{P}}[\log P(Y,Z|\theta )]+H(\tilde{P})\end{array}$$

称为$F$函数。式中$H(\tilde{P})=-E_{\tilde{P}}\log \tilde{P}(Z)$是分布$\tilde{P}(Z)$的熵。

第3步：引理9.1

  根据书中第9章的引理9.1：

  引理9.1 对于固定的$\theta$，存在唯一的分布${\tilde{P}}_{\theta }$极大化$F(\tilde{P},\theta )$，这时${\tilde{P}}_{\theta }$由下式给出：

$$\begin{array}{}\text{(9.34)}& {\tilde{P}}_{\theta }(Z)=P(Z|Y,\theta )\end{array}$$

并且${\tilde{P}}_{\theta }$随$\theta$连续变化。

$ \begin{aligned} \therefore F(\tilde{P}, \theta) &= E_{\tilde{P}}[\log P(Y, Z|\theta)] + H(\tilde{P}) \ &= E_{\tilde{P}}[\log P(Y,Z|\theta)] -E_{\tilde{P}} \log \tilde{P}(Z) \quad （F函数定义：H(\tilde{P}) = - E_{\tilde{P}} \log \tilde{P}(Z)）\ &= \sum_Z \log P(Y,Z|\theta) \tilde{P}_{\theta}(Z) - \sum_Z \log \tilde{P}(Z) \cdot \tilde{P}(Z) \end{aligned} $

根据引理9.1：${\tilde{P}}_{\theta }(Z)=P(Z|Y,\theta )$

$\begin{array}{rl}F(\tilde{P},\theta )& =\sum _Z\log P(Y,Z|\theta ){\tilde{P}}_{\theta }(Z)-\sum _Z\log \tilde{P}(Z)\cdot \tilde{P}(Z)\\ & =\sum _Z\log P(Y,Z|\theta )P(Z|Y,\theta )-\sum _Z\log P(Z|Y,\theta )\cdot P(Z|Y,\theta )\\ & =\sum _{Z}P(Z|Y,\theta )[\log P(Y,Z|\theta )-\log P(Z|Y,\theta )]\\ & =\sum _{Z}P(Z|Y,\theta )\log \frac{P(Y,Z|\theta )}{P(Z|Y,\theta )}\\ & =\sum _{Z}P(Z|Y,\theta )\log P(Y|\theta )\\ & =\log P(Y|\theta )\sum _{Z}P(Z|Y,\theta )\end{array}$

第4步：根据引理9.1，得证

根据引理9.1，可知：${\displaystyle \sum _{Z}P(Z|Y,\theta )=\sum _Z{\tilde{P}}_{\theta }(Z)=1}$

$\therefore F(\tilde{P},\theta )=\log P(Y|\theta )$，引理9.2得证。

习题9.3

已知观测数据 -67，-48，6，8，14，16，23，24，28，29，41，49，56，60，75，试估计两个分量的高斯混合模型的5个参数。

解答：

解答思路：

  两个分量的高斯混合模型一共有6个参数${\mu }_1,{\mu }_2,{\sigma }_1,{\sigma }_2,{\alpha }_1,{\alpha }_2$，其中${\alpha }_2$可由${\alpha }_2=1-{\alpha }_1$得到，故仅估计5个参数即可。

1. 写出高斯混合模型；
2. 写出高斯混合模型参数估计的EM算法；
3. 采用sklearn的GaussianMixture计算6个参数；
4. 采用自编程实现高斯混合模型的EM算法。

解答步骤：

第1步：高斯混合模型

  根据书中第9章的定义9.2的高斯混合模型：

  定义9.2（高斯混合模型） 高斯混合模型是指具有如下形式的概率分布模型：

$$P(y|\theta )=\sum _{k=1}^K{\alpha }_k\varphi (y|{\theta }_k)$$

其中，${\alpha }_k$是系数，${\alpha }_k⩾0$，${\displaystyle \sum _{k=1}^K{\alpha }_k=1}$；$\varphi (y|\theta )$是高斯分布密度，${\theta }_k=(u_k,{\sigma }_k^2)$，

$$\varphi (y|{\theta }_k)=\frac{1}{\sqrt{2\pi }{\sigma }_k}\exp (-\frac{(y-{\mu }_k{)}^2}{2{\sigma }_k^2})$$

称为第$k$个分模型。

从上述描述中可知，如果是2个高斯混合分模型，一共需要估计的参数有6个${\mu }_1,{\mu }_2,{\sigma }_1,{\sigma }_2,{\alpha }_1,{\alpha }_2$，其中${\alpha }_1+{\alpha }_2=1$

第2步：高斯混合模型参数估计的EM算法

  根据书中第9章的算法9.2：

算法9.2（高斯混合模型参数估计的EM算法）
输入：观测数据$y_1,y_2,\cdots ,y_N$，高斯混合模型；
输出：高斯混合模型参数。
（1）取参数的初始值开始迭代；
（2）E步：依据当前模型参数，计算分模型$k$对观测数据$y_i$的响应度

$${\hat{\gamma }}_{jk}=\frac{{\alpha }_k\varphi (y_j|{\theta }_k)}{{\displaystyle \sum _{k=1}^K{\alpha }_k\varphi (y_j|{\theta }_k)}},j=1,2,\cdots ,N;k=1,2,\cdots ,K$$

（3）M步：计算新一轮迭代的模型参数

$$\begin{gathered} {\hat{u}}_k=\frac{{\displaystyle \sum _{j=1}^N{\hat{\gamma }}_{jk}{y}_j}}{{\displaystyle \sum _{j=1}^N{\hat{\gamma }}_{jk}}},k=1,2,\cdots ,K \\ {\hat{\sigma }}_k^2=\frac{{\displaystyle \sum _{j=1}^N{\hat{\gamma }}_{jk}(y_j-u_k{)}^2}}{{\displaystyle \sum _{j=1}^N{\hat{\gamma }}_{jk}}},k=1,2,\cdots ,K \\ {\hat{\alpha }}_k=\frac{{\displaystyle \sum _{j=1}^N{\hat{\gamma }}_{jk}}}{N},k=1,2,\cdots ,K \end{gathered}$$

（4）重复第（2）步和第（3）步，直到收敛。

第3步：采用sklearn的GaussianMixture计算6个参数

from sklearn.mixture import GaussianMixture
import numpy as np
import matplotlib.pyplot as plt

# 初始化观测数据
data = np.array([-67, -48, 6, 8, 14, 16, 23, 24, 28,
                29, 41, 49, 56, 60, 75]).reshape(-1, 1)

# 设置n_components=2，表示两个分量高斯混合模型
gmm_model = GaussianMixture(n_components=2)
# 对模型进行参数估计
gmm_model.fit(data)
# 对数据进行聚类
labels = gmm_model.predict(data)

# 得到分类结果
print("分类结果：labels = {}\n".format(labels))
print("两个分量高斯混合模型的6个参数如下：")
# 得到参数u1,u2
print("means =", gmm_model.means_.reshape(1, -1))
# 得到参数sigma1, sigma1
print("covariances =", gmm_model.covariances_.reshape(1, -1))
# 得到参数a1, a2
print("weights = ", gmm_model.weights_.reshape(1, -1))

分类结果：labels = [0 0 1 1 1 1 1 1 1 1 1 1 1 1 1]

两个分量高斯混合模型的6个参数如下：
means = [[-57.51107027  32.98489643]]
covariances = [[ 90.24987882 429.45764867]]
weights =  [[0.13317238 0.86682762]]

# 绘制观测数据的聚类情况
for i in range(0, len(labels)):
    if labels[i] == 0:
        plt.scatter(i, data.take(i), s=15, c='red')
    elif labels[i] == 1:
        plt.scatter(i, data.take(i), s=15, c='blue')
plt.title('Gaussian Mixture Model')
plt.xlabel('x')
plt.ylabel('y')
plt.show()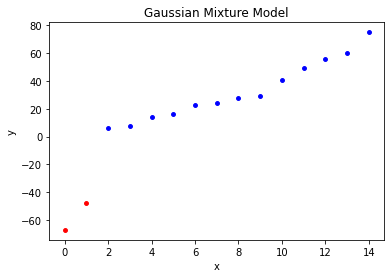

第4步：自编程实现高斯混合模型的EM算法

import numpy as np
import itertools


class MyGMM:
    def __init__(self, alphas_init, means_init, covariances_init, tol=1e-6, n_components=2, max_iter=50):
        # (1)设置参数的初始值
        # 分模型权重
        self.alpha_ = np.array(
            alphas_init, dtype="float16").reshape(n_components, 1)
        # 分模型均值
        self.mean_ = np.array(
            means_init, dtype="float16").reshape(n_components, 1)
        # 分模型标准差（方差的平方）
        self.covariances_ = np.array(
            covariances_init, dtype="float16").reshape(n_components, 1)
        # 迭代停止的阈值
        self.tol = tol
        # 高斯混合模型分量个数
        self.K = n_components
        # 最大迭代次数
        self.max_iter = max_iter
        # 观测数据
        self._y = None
        # 实际迭代次数
        self.n_iter_ = 0

    def gaussian(self, mean, convariances):
        """计算高斯分布概率密度"""
        return 1 / np.sqrt(2 * np.pi * convariances) * np.exp(
            -(self._y - mean) ** 2 / (2 * convariances))

    def update_r(self, mean, convariances, alpha):
        """更新r_jk 分模型k对观测数据yi的响应度"""
        r_jk = alpha * self.gaussian(mean, convariances)
        return r_jk / r_jk.sum(axis=0)

    def update_params(self, r):
        """更新u al si 每个分模型k的均值、权重、方差"""
        u = self.mean_[-1]
        _mean = ((r * self._y).sum(axis=1) / r.sum(axis=1)).reshape(self.K, 1)
        _covariances = ((r * (self._y - u) ** 2).sum(axis=1) /
                        r.sum(axis=1)).reshape(self.K, 1)
        _alpha = (r.sum(axis=1) / self._y.size).reshape(self.K, 1)
        return _mean, _covariances, _alpha

    def judge_stop(self, mean, covariances, alpha):
        """中止条件判断"""
        a = np.linalg.norm(self.mean_ - mean)
        b = np.linalg.norm(self.covariances_ - covariances)
        c = np.linalg.norm(self.alpha_ - alpha)
        return True if np.sqrt(a ** 2 + b ** 2 + c ** 2) < self.tol else False

    def fit(self, y):
        self._y = np.copy(np.array(y))
        """迭代训练获得预估参数"""
        # (2)E步：计算分模型k对观测数据yi的响应度
        r = self.update_r(self.mean_, self.covariances_, self.alpha_)
        # 更新r_jk 分模型k对观测数据yi的响应度
        _mean, _covariances, _alpha = self.update_params(r)
        # 更新u al si 每个分模型k的均值、权重、方差
        for i in range(self.max_iter):
            if not self.judge_stop(_mean, _covariances, _alpha):
                # (4)未达到阈值条件，重复迭代
                r = self.update_r(_mean, _covariances, _alpha)
                # (3)M步：计算新一轮迭代的模型参数
                _mean, _covariances, _alpha = self.update_params(r)
            else:
                # 达到阈值条件，停止迭代
                self.n_iter_ = i
                break

            self.mean_ = _mean
            self.covariances_ = _covariances
            self.alpha_ = _alpha

    def score(self):
        """计算该局部最优解的score，即似然函数值"""
        return (self.alpha_ * self.gaussian(self.mean_, self.covariances_)).sum()

# 观测数据
y = np.array([-67, -48, 6, 8, 14, 16, 23, 24, 28,
             29, 41, 49, 56, 60, 75]).reshape(1, 15)
# 预估均值和方差，以其邻域划分寻优范围
y_mean = y.mean() // 1
y_std = (y.std() ** 2) // 1

# 网格搜索，对不同的初值进行参数估计
alpha = [[i, 1 - i] for i in np.linspace(0.1, 0.9, 9)]
mean = [[y_mean + i, y_mean + j]
        for i in range(-10, 10, 5) for j in range(-10, 10, 5)]
covariances = [[y_std + i, y_std + j]
               for i in range(-1000, 1000, 500) for j in range(-1000, 1000, 500)]
results = []
for i in itertools.product(alpha, mean, covariances):
    init_alpha = i[0]
    init_mean = i[1]
    init_covariances = i[2]
    clf = MyGMM(alphas_init=init_alpha, means_init=init_mean, covariances_init=init_covariances,
                n_components=2, tol=1e-6)
    clf.fit(y)
    # 得到不同初值收敛的局部最优解
    results.append([clf.alpha_, clf.mean_, clf.covariances_, clf.score()])
# 根据score，从所有局部最优解找到相对最优解
best_value = max(results, key=lambda x: x[3])

print("alpha : {}".format(best_value[0].T))
print("mean : {}".format(best_value[1].T))
print("std : {}".format(best_value[2].T))

alpha : [[0.56950675 0.43049325]]
mean : [[27.41762854 12.35515017]]
std : [[ 268.17311145 2772.33989897]]

习题9.4

  EM算法可以用到朴素贝叶斯法的非监督学习，试写出其算法。

解答：

解答思路：
参考： http://www.cs.columbia.edu/~mcollins/em.pdf

1. 列出EM算法；
2. 列出朴素贝叶斯算法；
3. 推导朴素贝叶斯的EM算法。

解答步骤：

第1步：EM算法

  根据书中第9章的算法9.1的EM算法：

算法9.1（EM算法）
输入：观测变量数据$Y$，隐变量数据$Z$，联合分布$P(Y,Z|\theta )$，条件分布$P(Z|Y,\theta )$；
输出：模型参数$\theta$。
（1）选择参数的初值${\theta }^{(0)}$，开始迭代；
（2）E步：记${\theta }^{(i)}$为第$i$次迭代参数$\theta$的估计值，在第$i+1$次迭代的E步，计算

$$\begin{array}{rl}Q(\theta ,{\theta }^{(i)})& =E_Z[\log P(Y,Z|\theta )|Y,{\theta }^{(i)}]\\ & =\sum _z\log P(Y,Z|\theta )P(Z|Y,{\theta }^{(i)})\end{array}$$

这里，$P(Z|Y,\theta )$是在给定观测数据$Y$和当前的参数估计${\theta }^{(i)}$下隐变量数据$Z$的条件概率分布；
（3）M步：求使$Q(\theta ,{\theta }^{(i)})$极大化的$\theta$，确定第$i+1$次迭代的参数的估计值${\theta }^{(i+1)}$

$${\theta }^{(i+1)}=\arg \underset{\theta }{max}Q(\theta ,{\theta }^{(i)})$$

（4）重复第（2）步和第（3）步，直至收敛。

第2步：朴素贝叶斯算法

  根据书中第4章的算法4.1的朴素贝叶斯算法：

算法4.1（朴素贝叶斯算法）
输入：训练数据$T=(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)$，其中$x_i=(x_i^{(1)},x_i^{(2)},\cdots ,x_i^{(n)}{)}^T$，$x_i^{(j)}$是第$i$个样本的第$j$个特征，$x_i^{(j)}\in \{a_{j1},a_{j2},\cdots ,a_{j{S}_j}\}$，$a_{jl}$是第$j$个特征可能取的第$l$个值，$j=1,2,\cdots ,n$，$l=1,2,\cdots ,S_j$，$y_i\in \{c_1,c_2,\cdots ,c_K\}$；实例$x$；
输出：实例$x$的分类。
（1）计算先验概率及条件概率

$$\begin{gathered} P(Y=c_k)=\frac{{\displaystyle \sum _{i=1}^{N}I(y_i=c_k)}}{N},k=1,2,\cdots ,K \\ P(X^{(j)}=a_{jl}|Y=c_k)=\frac{{\displaystyle \sum _{i=1}^{N}I(x_i^{(j)}=a_{jl},y_i=c_k)}}{{\displaystyle \sum _{i=1}^{N}I(y_i=c_k)}} \\ j=1,2,\cdots ,n;l=1,2,\cdots ,S_j;k=1,2,\cdots ,K \end{gathered}$$

（2）对于给定的实例$x=(x^{(1)},x^{(2)},\cdots ,x^{(n)}{)}^T$，计算

$$P(Y=c_k)\prod _{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k),k=1,2,\cdots ,K$$

（3）确定实例$x$的类

$$y=\arg \underset{c_k}{max}P(Y=c_k)\prod _{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k)$$

第3步：推导朴素贝叶斯的EM算法

推导思路：

1. 假设隐变量数据是$y\in \mathcal{Y}=\{c_1,c_2,\cdots ,c_K\}$
2. 设置初值，$P^{(0)}(Y=y)⩾0$和$P_j^{(0)}(X=x|Y=y)⩾0$，其中$j=1,2,\cdots ,n$，满足

$$\begin{gathered} \sum _{y\in \mathcal{Y}}{P}^{(0)}(Y=y)=1 \\ \sum _{x\in \{-1,+1\}}{P}_j^{(0)}(X=x|Y=y)=1 \end{gathered}$$

3. 根据概率公式，可知概率

$$\delta (y|i)=P(Y=y|X=x_i,{\theta }^{(t)})=\frac{{\displaystyle P^{(t)}(Y=y)\prod _{j=1}^n{P}_j^{(t)}(X=x_i^{(j)}|Y=y)}}{{\displaystyle \sum _{y\in \mathcal{Y}}{P}^{(t)}(Y=y)\prod _{j=1}^n{P}_j^{(t)}(X=x_i^{(j)}|Y=y)}}$$

其中$\theta$表示朴素贝叶斯模型中所有的参数向量 4. 迭代更新参数

$$\begin{gathered} P^{(t+1)}(Y=y)=\frac{1}{N}\sum _{i=1}^N\delta (y|i) \\ {P}_j^{(t+1)}(X=x_i^{(j)}|y)=\frac{{\displaystyle \sum _{i=1}^{N}P(X=x_i^{(j)})\delta (y|i)}}{{\displaystyle \sum _{i=1}^N\delta (y|i)}} \end{gathered}$$

5. 计算似然函数，得到使得似然函数最大的$\theta$，重复第3步和第4步，直至收敛

$$\begin{array}{rl}{\theta }^{\ast }& =\arg \underset{\theta \in \mathrm{\Omega }}{max}L(\theta )\\ & =\arg \underset{\theta \in \mathrm{\Omega }}{max}\sum _{i=1}^N\sum _{y\in \mathcal{Y}}\delta (y|i)\log (P(Y=y)\prod _{j=1}^n{P}_j(X=x_i^{(j)}|Y=y))\end{array}$$

所以，朴素贝叶斯的EM算法如下：

输入：隐变量数据是$y\in \mathcal{Y}=\{c_1,c_2,\cdots ,c_K\}$，$x\in \mathcal{X}=(x_1,x_2,\cdots ,x_N)$，输入空间$\mathcal{X}\subset R^n$为$n$维向量的集合，$x=(x^{(1)},x^{(2)},\cdots ,x^{(n)}{)}^T$，$x^{(i)}$取值范围是$\{-1,+1\}$；
输出：参数$P^{(t+1)}(Y=y)$，$P_j^{(t+1)}(X=x_i^{(j)}|y)$；
（1）选择参数的初值$P^{(0)}(Y=y)⩾0$和$P_j^{(0)}(X=x|Y=y)⩾0$，开始迭代；
（2）E步：记${\theta }^{(t)}$为第$t$次迭代参数$\theta$的估计值，在第$t+1$次迭代的E步，计算

$$\delta (y|i)=P(Y=y|X=x_i,{\theta }^{(t)})=\frac{{\displaystyle P^{(t)}(Y=y)\prod _{j=1}^n{P}_j^{(t)}(X=x_i^{(j)}|Y=y)}}{{\displaystyle \sum _{y\in \mathcal{Y}}{P}^{(t)}(Y=y)\prod _{j=1}^n{P}_j^{(t)}(X=x_i^{(j)}|Y=y)}}$$

（3）M步：求使$Q(\theta ,{\theta }^{(t)})$极大化的$\theta$，确定第$t+1$次迭代的参数的估计值

$$\begin{gathered} P^{(t+1)}(Y=y)=\frac{1}{N}\sum _{i=1}^N\delta (y|i) \\ {P}_j^{(t+1)}(X=x_i^{(j)}|y)=\frac{{\displaystyle \sum _{i=1}^{N}P(X=x_i^{(j)})\delta (y|i)}}{{\displaystyle \sum _{i=1}^N\delta (y|i)}} \end{gathered}$$

（4）重复第（2）步和第（3）步，直至收敛。