第23章前馈神经网络

习题23.1

  构造前馈神经网络实现逻辑表达式XNOR，使用S型函数为激活函数。

解答：

解答思路：

1. 给出同或函数(XNOR)的输入和输出
2. 用神经网络实现的门表示XNOR
3. 设计神经网络实现XNOR
4. 自编程实现二层前馈神经网络表示XNOR

解答步骤：

第1步: 给出同或函数(XNOR)的输入和输出

  对于同或函数(XNOR)，全部的输入与对应的输出如下：

$x_1$	$x_2$	$y=x_1\odot x_2$
0	0	1
0	1	0
1	0	0
1	1	1

第2步: 用神经网络实现的门表示XNOR

  XNOR（同或门）和XOR（异或门）由于都是线性不可分的，不能由一层神经网络实现，但它们可由一层神经网络实现的门组合实现。

  一层神经网络可实现的门包括AND（与门，用$x_1\wedge x_2$表示）、NOR（或非门，用$\overline{x_1\vee x_2}$表示）、OR（或门，用$x_1\vee x_2$表示）等。

  同或函数可表示：

$$x_1\odot x_2=(x_1\wedge x_2)\vee \overline{x_1\vee x_2}$$

第3步: 设计神经网络实现XNOR

  根据书中第23.1.1节的S型函数的定义：

S型函数（sigmoid function）又称为逻辑斯谛函数（logistic function），是定义式如下的非线性函数：

$$\begin{array}{}\text{(23.14)}& a(z)=\sigma (z)=\frac{1}{1+e^{-z}}\end{array}$$

其中，$z$是自变量或输入，$\sigma (z)$是因变量或输出。函数的定义域为$(-\mathrm{\infty },\mathrm{\infty })$，值域为$(0,1)$。

  可知：

$$\begin{gathered} \text{sigmoid}(10)\approx 1 \\ \text{sigmoid}(-10)\approx 0 \end{gathered}$$

  可设计如下二层前馈神经网络表示XNOR：

$$\begin{gathered} h_1=x_1\wedge x_2 \\ {h}_2=\overline{x_1\vee x_2} \\ y=h_1\vee h_2 \end{gathered}$$

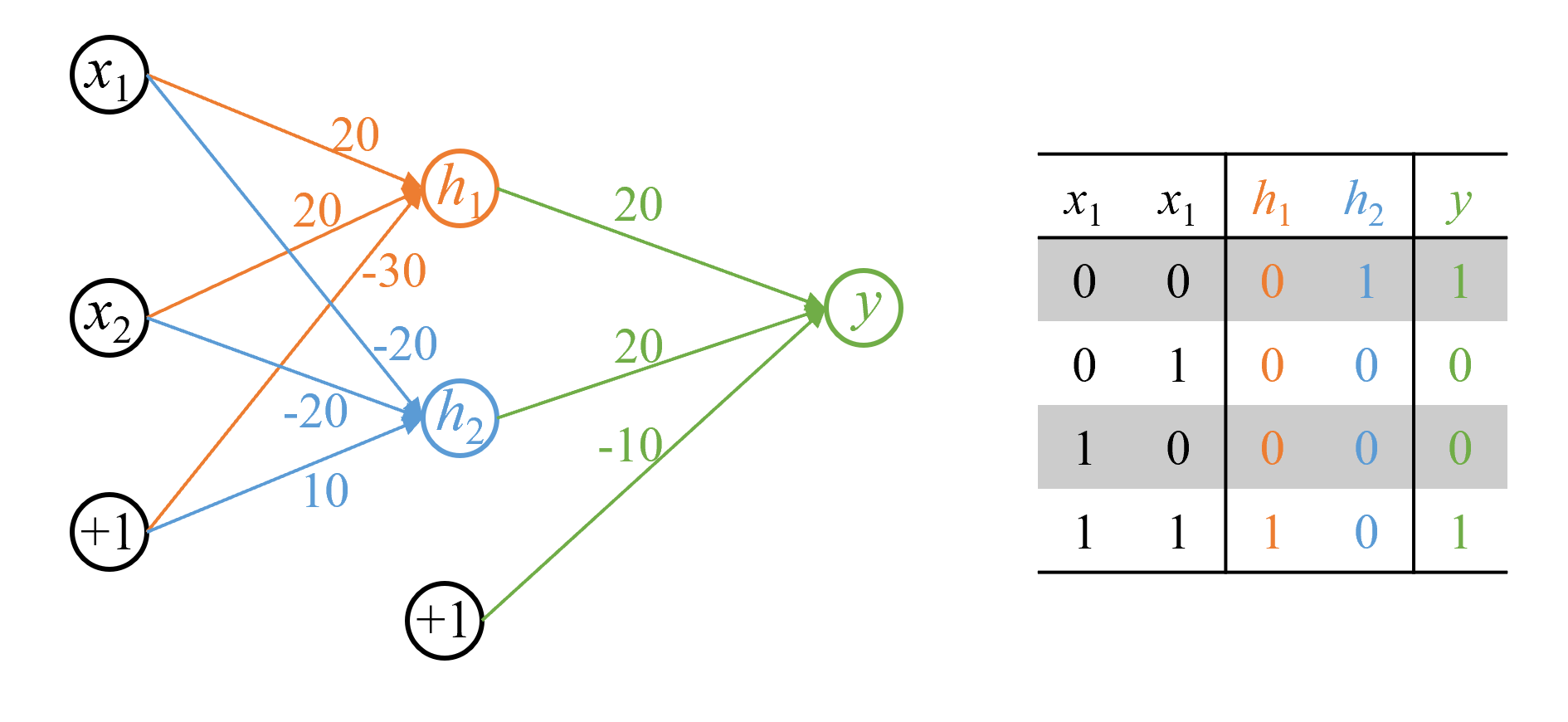
  根据书中第23.1.1节的二层前馈神经网络的矩阵表示：

二层前馈神经网络也可以用矩阵来表示，简称矩阵表示：

$$\begin{gathered} {\mathit{h}}^{(1)}=f^{(1)}(\mathit{x})=a(z^{(1)})=a({{\mathit{W}}^{(1)}}^T\mathit{x}+{\mathit{b}}^{(1)}) \\ \mathit{y}=f^{(2)}({\mathit{h}}^{(1)})=g(z^{(2)})=g({{\mathit{W}}^{(2)}}^T\mathit{h}+{\mathit{b}}^{(2)}) \end{gathered}$$

  其中，

$$\begin{gathered} \mathit{x}=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right] \\ \mathit{h}=\left[\begin{array}{c}{h}_1\\ h_2\end{array}\right] \\ {\mathit{W}}^{\mathbf{(}\mathbf{1}\mathbf{)}}=\left[\begin{array}{cc}20& -20\\ 20& -20\end{array}\right] \\ {\mathit{W}}^{\mathbf{(}\mathbf{2}\mathbf{)}}=\left[\begin{array}{c}20\\ 20\end{array}\right] \\ {\mathit{b}}^{\mathbf{(}\mathbf{1}\mathbf{)}}=\left[\begin{array}{c}-30\\ 10\end{array}\right] \\ {\mathit{b}}^{\mathbf{(}\mathbf{2}\mathbf{)}}=[-10] \end{gathered}$$

第4步: 自编程实现二层前馈神经网络表示XNOR

import numpy as np

# 定义网络的权重W和偏置b
W1 = np.array([[20, -20], [20, -20]])
b1 = np.array([[-30], [10]])
W2 = np.array([[20], [20]])
b2 = np.array([[-10]])

def sigmoid(x):
    s = 1 / (1 + np.exp(-x))
    return s

def dnn_xnor(X):
    Z1 = W1.T.dot(X) + b1
    H = sigmoid(Z1)

    Z2 = W2.T.dot(H) + b2
    Y = sigmoid(Z2)
    
    return Y

X = np.array([[0, 0, 1, 1],
              [0, 1, 0, 1]])

with np.printoptions(suppress=True):
    result = dnn_xnor(X)
    print(result)

[[0.99995456 0.00004548 0.00004548 0.99995456]]

习题23.2

  写出多标签分类学习中的损失函数以及损失函数对输出变量的导数。

解答：

解答思路：

1. 给出前馈神经网络学习在多标签分类时的模型
2. 写出多标签分类学习中的损失函数
3. 求损失函数对输出变量的导数

解答步骤：

第1步: 前馈神经网络学习在多标签分类时的模型

  根据书中第23.1.1节的前馈神经网络学习在多标签分类时的模型：

  用于多标签分类（multi-label classification）。神经网络的输出层有 $l$ 个神经元，每个神经元的输出是一个概率值。神经网络表示为 $\mathit{p}=[P(y_k=1|\mathit{x})]=f(\mathit{x})$，其中$y_k\in \{0,1\},k=1,2,\cdots ,l$，满足条件

$$0<P(y_k=1|\mathit{x})<1,P(y_k=1|\mathit{x})+P(y_k=0|\mathit{x})=1,k=1,2,\cdots ,l$$

$[P(y_1=1|\mathit{x}),P(y_2=1|\mathit{x}),\cdots ,P(y_l=1|\mathit{x})]$ 表示输入 $\mathit{x}$ 分别属于1个类别的概率。预测时给定输入 $\mathit{x}$，计算其属于各个类别的概率。将输入分到概率大于0.5的所有类别，这时输入可以被分到多个类别（赋予多个标签）。

第2步: 写出多标签分类学习中的损失函数

  多标签分类时，输出层有$l$个神经元，每个神经元输出是一个概率值，表示属于各标签的概率。多标签分类学习中的损失函数通常为二元交叉熵（Binary Cross-Entropy, BCE）损失函数：

$$\text{BCELoss}=-\frac{1}{N}\sum _{i=1}^N\sum _{k=1}^l[y_{ik}\log (p_{ik})+(1-y_{ik})\log (1-p_{ik})]$$

其中，$N$是样本的数量，$l$是标签的数量，$y_{ik}$是第$i$个样本的第$k$个标签的真实值，$p_{ik}$是第$i$样本属于第$k$个标签的预测概率。

第3步: 求损失函数对输出变量的导数

  输出层的输出变量是经过S型激活函数变换后的值，即$p_{ik}$，则BCELoss对$p_{ik}$求导：

$$\begin{array}{rl}\frac{\partial \text{BCELoss}}{\partial p_{ik}}& =-\frac{1}{N}(\frac{y_{ik}}{p_{ik}}-\frac{1-y_{ik}}{1-p_{ik}})\\ & =-\frac{1}{N}\left(\frac{y_{ik}-y_{ik}{p}_{ik}-p_{ik}+y_{ik}{p}_{ik}}{p_{ik}(1-p_{ik})}\right)\\ & =\frac{p_{ik}-y_{ik}}{N{p}_{ik}(1-p_{ik})}\end{array}$$

即：

$$\frac{\partial \text{BCELoss}}{\partial p_{ik}}=\frac{p_{ik}-y_{ik}}{N{p}_{ik}(1-p_{ik})}$$

习题23.3

  实现前馈神经网络的反向传播算法，使用MNIST数据构建手写数字识别网络。

解答：

解答思路：

1. 给出MNIST手写数字识别网络
2. 给出前馈神经网络的反向传播算法
3. 自编程实现使用MNIST数据集构建手写数字识别网络

解答步骤：

第1步: MNIST手写数据识别网络

  根据书中第23章例23.4给出MNIST手写数字识别网络：

  MNIST是一个机器学习标准数据集。每一个样本由一个像素为28 $\times$ 28 的手写数字灰度图像以及的0~9之间的标签组成，像素取值为0~255。
  可以构建图23.14所示的前馈神经网络对MNIST的手写数字进行识别，是一个多标签分类模型。输入层是一个$28\times 28=784$维向量，取自一个图像，每一维对应一个像素。第一层和第二层是隐层，各自有100个神经元和50个神经元，其激活函数都是S型函数。第三层是输出层，有10个神经元，其激活函数也是S型函数。给定一个图像，神经网络可以计算出其属于0~9类的概率，将图像赋予概率最大的标签。

第2步：前馈神经网络的反向传播算法

  根据书中第23.2.3节的算法23.3的前馈神经网络的反向传播算法：

算法23.3 （前馈神经网络的反向传播算法）
输入：神经网络$f(\mathit{x};\mathit{\theta })$，参数向量$\mathit{\theta }$，一个样本$(\mathit{x},\mathit{y})$
输出：更新的参数向量$\mathit{\theta }$
超参数：学习率$\eta$

1. 正向传播，得到各层输出${\mathit{h}}^{(1)},{\mathit{h}}^{(2)},\cdots ,{\mathit{h}}^{(s)}$

$${\mathit{h}}^{(0)}=\mathit{x}$$

For $t=1,2,\cdots ,s$，do {

$$\begin{gathered} z^{(t)}={\mathit{W}}^{(t)}{\mathit{h}}^{(t-1)}+{\mathit{b}}^{(t)} \\ {\mathit{h}}^{(t)}=a(z^{(t)}) \end{gathered}$$

} 2. 反向传播，得到各层误差${\mathit{\delta }}^{(s)},\cdots ,{\mathit{\delta }}^{(2)},{\mathit{\delta }}^{(1)}$，同时计算各层的梯度，更新各层的参数。
计算输出层的误差

$${\mathit{\delta }}^{(s)}={\mathit{h}}^{(s)}-\mathit{y}$$

For $t=s,\cdots ,2,1$，do {
  计算第$t$层的梯度

$$\begin{gathered} {\mathrm{\nabla }}_{{\mathit{W}}^{(t)}}L={\mathit{\delta }}^{(t)}\cdot {{\mathit{h}}^{(t-1)}}^T \\ {\mathrm{\nabla }}_{{\mathit{b}}^{(t)}}L={\mathit{\delta }}^{(t)} \end{gathered}$$

  根据梯度下降公式更新第$t$层的参数

$$\begin{gathered} {\mathit{W}}^{(t)}\leftarrow {\mathit{W}}^{(t)}-\eta {\mathrm{\nabla }}_{{\mathit{W}}^{(t)}}L \\ {\mathit{b}}^{(t)}\leftarrow {\mathit{b}}^{(t)}-\eta {\mathrm{\nabla }}_{{\mathit{b}}^{(t)}}L \end{gathered}$$

   If ($t>1$) {
     将第$t$层的误差传到第$t-1$层

$${\mathit{\delta }}^{(t-1)}=\frac{\partial a}{\partial z^{(t-1)}}\odot ({{\mathit{W}}^{(t)}}^T\cdot {\mathit{\delta }}^{(t)})$$

  }
} 3. 返回更新的参数向量

第3步：自编程实现使用MNIST数据集构建手写数字识别网络

import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelBinarizer

from tqdm import tqdm

np.random.seed(2023)

class NeuralNetwork:
    def __init__(self, layers, alpha=0.1):
        # 网络层的神经元个数，其中第一层和第二层是隐层
        self.layers = layers
        # 学习率
        self.alpha = alpha
        # 权重
        self.weights = []
        # 偏置
        self.biases = []
        # 初始化权重和偏置
        for i in range(1, len(layers)):
            self.weights.append(np.random.randn(layers[i-1], layers[i]))
            self.biases.append(np.random.randn(layers[i]))

    def sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

    def sigmoid_derivative(self, x):
        return x * (1 - x)
    
    def feedforward(self, inputs):
        '''
        （1）正向传播
        '''
        self.activations = [inputs]
        self.weighted_inputs = []
        for i in range(len(self.weights)):
            weighted_input = np.dot(self.activations[-1], self.weights[i]) + self.biases[i]
            self.weighted_inputs.append(weighted_input)
            # 得到各层的输出h
            activation = self.sigmoid(weighted_input)
            self.activations.append(activation)
   
        return self.activations[-1]

    def backpropagate(self, expected):
        '''
        （2）反向传播
        '''
        # 计算各层的误差
        errors = [expected - self.activations[-1]]
        # 计算各层的梯度
        deltas = [errors[-1] * self.sigmoid_derivative(self.activations[-1])]
        
        for i in range(len(self.weights)-1, 0, -1):
            error = deltas[-1].dot(self.weights[i].T)
            errors.append(error)
            delta = errors[-1] * self.sigmoid_derivative(self.activations[i])
            deltas.append(delta)
        deltas.reverse()
        
        for i in range(len(self.weights)):
            # 更新参数
            self.weights[i] += self.alpha * np.array([self.activations[i]]).T.dot(np.array([deltas[i]]))
            self.biases[i] += self.alpha * np.sum(deltas[i], axis=0)

    def train(self, inputs, expected_outputs, epochs):
        for i in tqdm(range(epochs)):
            for j in range(len(inputs)):
                self.feedforward(inputs[j])
                self.backpropagate(expected_outputs[j])

# 加载MNIST手写数字数据集
mnist = fetch_openml('mnist_784', parser='auto')
X = mnist.data.astype('float32') / 255.0
y = mnist.target.astype('int')

# 划分训练集和测试集
lb = LabelBinarizer()
y = lb.fit_transform(y)
X = np.array(X)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 训练神经网络，其中第一层和第二层各有100个神经元和50个神经元
nn = NeuralNetwork([784, 100, 50, 10], alpha=0.1)
nn.train(X_train, y_train, epochs=10)

100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 10/10 [02:21<00:00, 14.20s/it]

# 使用测试集对模型进行评估
correct = 0

for i in range(len(X_test)):
    output = nn.feedforward(X_test[i])
    prediction = np.argmax(output)
    actual = np.argmax(y_test[i])
    if prediction == actual:
        correct += 1

accuracy = correct / len(X_test) * 100
print("Accuracy: {:.2f} %".format(accuracy))

Accuracy: 93.94 %

习题23.4

  写出S型函数的正向传播和反向传播的计算图。

解答：

解答思路：

1. 写出S型函数的正向传播计算图
2. 写出S型函数的反向传播计算图

解答步骤：

第1步: 写出S型函数的正向传播计算图

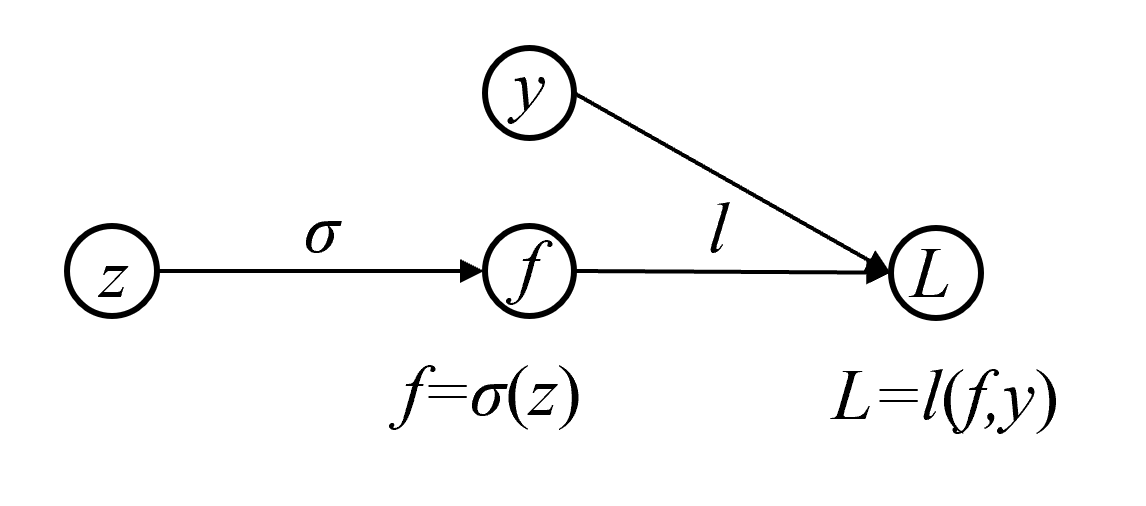
  根据书中第23.2.4节给出了S型函数的计算图例：

  起点$z$, $y$是输入变量，终点$L$是输出变量，中间结点$f$是中间变量。变量$f$由S型函数$f=\sigma (z)$决定，变量$L$由损失函数$L=l(f,y)$决定。

  根据书中第23.2.4节给出的计算图的正向传播：

  在计算图上进行的正向传播就是计算复合函数 $L=l(\sigma (z),y)$ 的过程。从起点 $z,y$ 开始，顺着有向边，在结点 $f,L$ 依次进行计算，先后得到函数$f,L$；其中先对 $z$ 计算 $f(z)$ 得到 $f$，然后对 $f$ 和 $y$ 计算 $l(f,y)$ 得到 $L$。

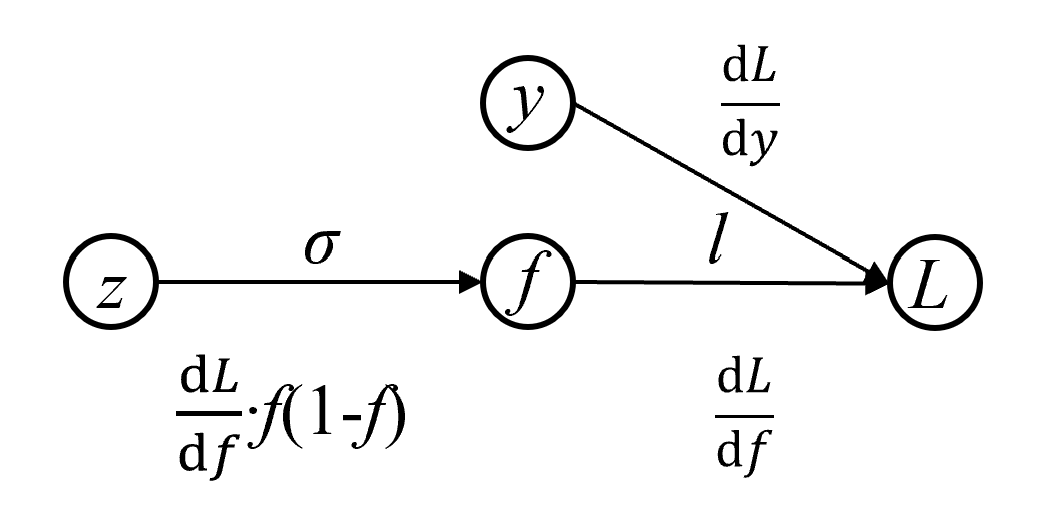
第2步: 写出S型函数的反向传播计算图

  根据书中第23.2.4节给出的计算图的方向传播：

  反向传播就是计算复合函数$L=l(\sigma (z),y)$ 对变量的梯度的过程。从终止起点 $L$ 出发，逆着有向边，在结点 $y,f,z$ 依次进行，向后得到梯度${\displaystyle \frac{\text{d}L}{\text{d}y},\frac{\text{d}L}{\text{d}f},\frac{\text{d}L}{\text{d}z}}$；其中先根据定义计算${\displaystyle \frac{\text{d}L}{\text{d}y},\frac{\text{d}L}{\text{d}f}}$，再利用链式规则计算${\displaystyle \frac{\text{d}L}{\text{d}z}}$：

$$\frac{\text{d}L}{\text{d}z}=\frac{\text{d}L}{\text{d}f}\cdot \frac{\text{d}L}{\text{d}f}\cdot f(1-f)$$

梯度${\displaystyle \frac{\text{d}L}{\text{d}f}}$在结点 $f$ 的反向传播变为梯度的$f(1-f)$ 倍，传到输入结点 $z$。

习题23.5

  图23.31是3类分类的正向传播计算图，试写出它的反向传播计算图。这里使用软最大化函数和交叉熵损失。

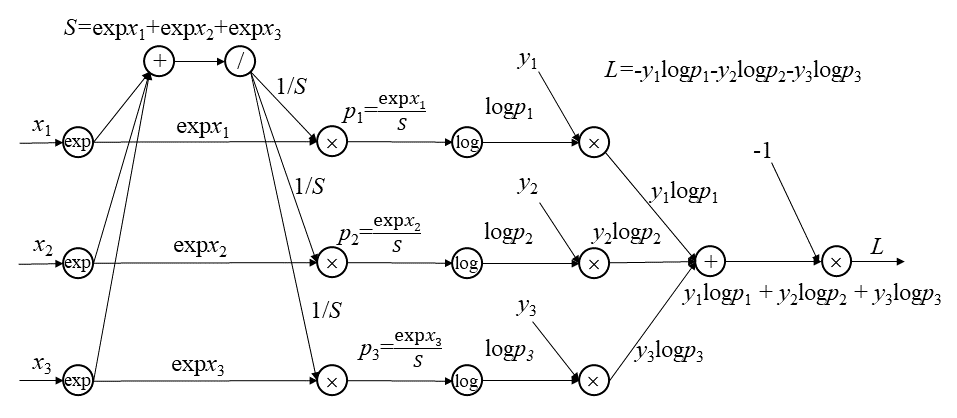
解答：

解答思路：

1. 根据正向传播计算图，根据链式法则，逐步求导给出各层的梯度
2. 绘制反向传播的计算图

解答步骤：

第1步：根据正向传播计算图，根据链式法则，逐步求导给出各层的梯度

  见下图中各层的梯度计算结果。

第2步：绘制反向传播的计算图

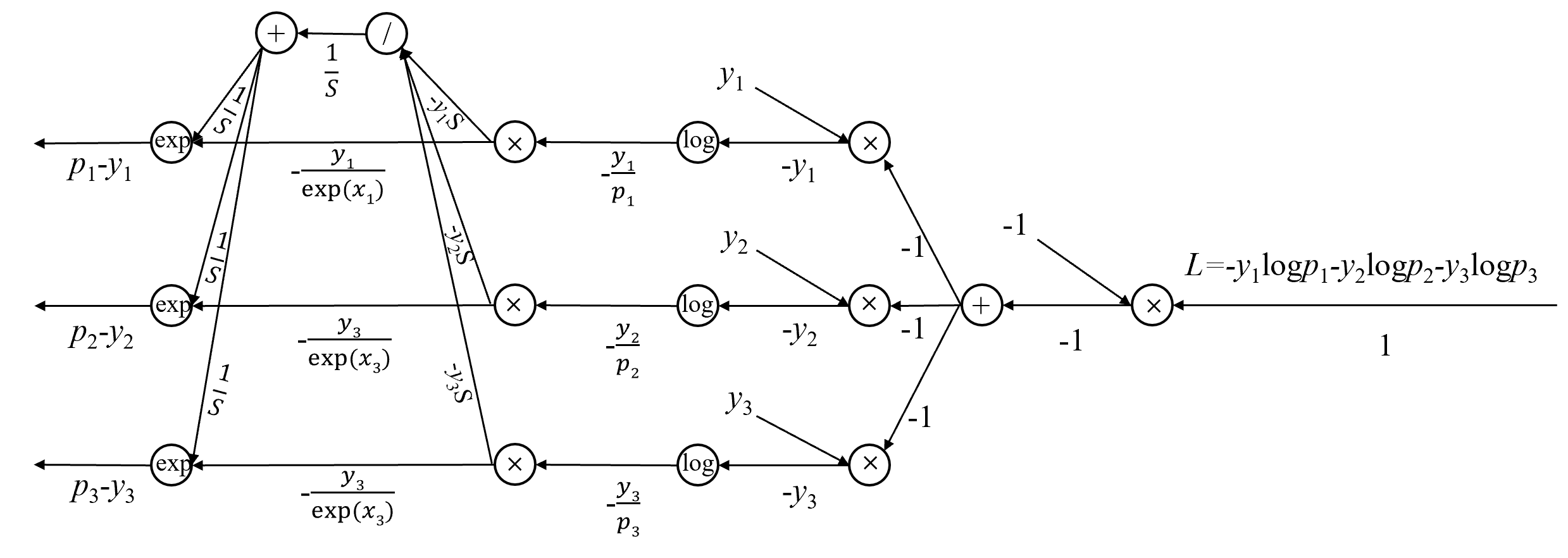
习题23.6

  写出批量归一化的反向传播算法。

解答：

解答思路：

1. 给出批量归一化算法
2. 求批量归一化层的梯度
3. 写出全连接层的梯度
4. 写出批量归一化的反向传播算法

解答步骤：

第1步：批量归一化算法

  根据书中第23.2.5节的算法23.4的批量归一化算法：

算法23.4（批量归一化）
输入：神经网络结构$f(\mathit{x};\mathit{\theta })$，训练集，测试样本。
输出：对测试样本的预测值。
超参数：批量容量的大小 $n$。
{
  初始化参数$\mathit{\theta },\varphi$，其中$\varphi =\{{\gamma }^{(t)},{\beta }^{(t)}{\}}_{t=1}^{s-1}$
  For each (批量$b$) {
    For $t = 1, 2, \cdots, s - 1 $ {
      针对批量$b$计算第$t$层净输入的均值${\mathit{u}}^{(t)}$和方差${{\mathit{\sigma }}^{\mathbf{2}}}^{\mathbf{(}\mathit{t}\mathbf{)}}$
      进行第$t$层的批量归一化，得到批量净输入

$$z_j^{(t)}\to {\overline{z}}_j^{(t)}\to {\tilde{z}}_j^{(t)},j=1,2,\cdots ,n$$

    }
  }
  构建训练神经网络$f_{\text{Tr}}(\mathit{x};\mathit{\theta },\varphi )$
  使用随机梯度下降法训练$f_{\text{Tr}}(\mathit{x};\mathit{\theta },\varphi )$，估计所有参数$\mathit{\theta },\varphi$
  For $t=1,2,\cdots ,s-1$ {
    针对所有批量计算$t$层净输入的期待的均值$E_b({\mathit{u}}^{(t)})$和方差$E_b({{\mathit{\sigma }}^2}^{(t)})$
    针对测试样本，进行第$t$层的批量归一化，得到净输入

$$z_j^{(t)}\to {\overline{z}}_j^{(t)}\to {\tilde{z}}_j^{(t)},j=1,2,\cdots ,n$$

  }
  构建推理神经网络$f_{\text{Inf}}(\mathit{x};\mathit{\theta },\varphi )$
  输出$f_{\text{Inf}}(\mathit{x};\mathit{\theta },\varphi )$对测试样本的预测值
}

第2步：求批量归一化层的梯度

  根据书中第404页图23.25（批量归一化层的正向计算图），求每一步的反向梯度。

  假设损失函数为$L$，已知$L$对${\tilde{z}}_j$的偏导${\displaystyle \frac{\partial L}{\partial {\tilde{z}}_j}}$，求${\displaystyle \frac{\partial L}{\partial \gamma },\frac{\partial L}{\partial \beta },\frac{\partial L}{\partial {\overline{z}}_j}}$，可得：

$$\begin{array}{rl}\frac{\partial L}{\partial \gamma }& =\sum _{j=1}^N\frac{\partial L}{\partial {\tilde{z}}_j}{\overline{z}}_j\\ \frac{\partial L}{\partial \beta }& =\sum _{i=1}^N\frac{\partial L}{\partial {\tilde{z}}_j}\\ \frac{\partial L}{\partial {\overline{z}}_j}& =\frac{\partial L}{\partial {\tilde{z}}_j}\gamma \end{array}$$

  根据书中第403页的公式23.61：

$$\begin{array}{}\text{(23.61)}& {\overline{z}}_j=\frac{z_j-u}{\sqrt{{\sigma }^2+ϵ}},j=1,2,\cdots ,n\end{array}$$

可将${\displaystyle \frac{\partial L}{\partial z_j}}$分成${\overline{z}}_j,\mu ,{\sigma }^2$三部分进行求解，可得：

$$\frac{\partial L}{\partial z_j}=\frac{\partial L}{\partial {\overline{z}}_j}\frac{1}{\sqrt{{\sigma }^2+ϵ}}+\frac{\partial L}{\partial \mu }\cdot \frac{\partial \mu }{\partial z_j}+\frac{\partial L}{\partial {\sigma }^2}\cdot \frac{\partial {\sigma }^2}{\partial z_j}$$

  根据书中第403页的公式23.59, 23.60：

$$\begin{array}{}\text{(23.59)}& u=\frac{1}{n}\sum _{j=1}^n{z}_j\end{array}$$$$\begin{array}{}\text{(23.60)}& {\sigma }^2=\frac{1}{n-1}\sum _{j=1}^n(z_j-u{)}^2\end{array}$$

可分别求${\displaystyle \frac{\partial L}{\partial \mu },\frac{\partial \mu }{\partial z_j},\frac{\partial L}{\partial {\sigma }^2},\frac{\partial {\sigma }^2}{\partial z_j}}$，可得：

$$\begin{array}{rl}\frac{\partial L}{\partial \mu }& =\sum _{j=1}^n\frac{\partial L}{\partial {\overline{z}}_j}\cdot \frac{-1}{\sqrt{{\sigma }^2+ϵ}}+\frac{\partial L}{\partial {\sigma }^2}\frac{{\displaystyle -\sum _{j=1}^{n}2(z_j-\mu )}}{n}\\ \frac{\partial \mu }{\partial z_j}& =\frac{1}{n}\\ \frac{\partial L}{\partial {\sigma }^2}& =\sum _{j=1}^n\frac{\partial L}{\partial {\overline{z}}_j}\cdot (z_j-\mu )\cdot \frac{-({\sigma }^2+ϵ{)}^{-3/2}}{2}\\ \frac{\partial {\sigma }^2}{\partial z_j}& =\frac{2(z_j-\mu )}{n}\\ \frac{\partial L}{\partial z_j}& =\frac{\partial L}{\partial {\overline{z}}_j}\frac{1}{\sqrt{{\sigma }^2+ϵ}}+\frac{\partial L}{\partial \mu }\cdot \frac{1}{n}+\frac{\partial L}{\partial {\sigma }^2}\cdot \frac{2(z_j-\mu )}{n}\end{array}$$

第3步：结合批量归一化层的梯度，写出全连接层的梯度

第$t$层的误差为：

$${\delta }_j^{(t)}=\frac{\partial L}{\partial z_j^{(t)}}$$

参数$W$的梯度为：

$$\begin{array}{rl}\frac{\partial L}{\partial W^{(t)}}& =\sum _{j=1}^n\frac{\partial L}{\partial z_j^{(t)}}\frac{\partial z_j^{(t)}}{\partial W^{(t)}}\\ & =\sum _{j=1}^n{\delta }_j^{(t)}\cdot h_j^{(t-1)}\end{array}$$

参数$b$的梯度为：

$$\begin{array}{rl}\frac{\partial L}{\partial b^{(t)}}& =\sum _{j=1}^n\frac{\partial L}{\partial z_j^{(t)}}\frac{\partial z_j^{(t)}}{\partial b^{(t)}}\\ & =\sum _{j=1}^n{\delta }_j^{(t)}\end{array}$$

$t+1$层和$t$层之间的关系为：

$${\delta }_j^{(t)}=\frac{\partial a}{\partial {\tilde{z}}_j^{(t)}}\cdot \frac{\partial {\tilde{z}}_j^{(t)}}{\partial z_j^{(t)}}\cdot W^{(t+1)}\cdot {\delta }_j^{(t+1)}$$

其中，$a$表示激活函数。

第4步：写出批量归一化的反向传播算法

输入：神经网络结构$f(\mathit{x};\mathit{\theta },\varphi )$，训练集$(\mathit{x},\mathit{y})$
输出：参数向量$\mathit{\theta },\varphi$
超参数：学习率$\eta$，批量容量的大小$n$

算法步骤：

1. 初始化参数$\mathit{\theta },\varphi$，其中$\varphi =\{{\gamma }^{(t)},{\beta }^{(t)}{\}}_{t=1}^{s-1}$
2. 计算输出层误差

$${\delta }^{(s)}=h^{(s)}-y$$

3. For each(批量 $b$) {
     For $t=s,\cdots ,2,1$， do {
       计算第$t$层的梯度 ${\mathrm{\nabla }}_{W^{(t)}}L,{\mathrm{\nabla }}_{b^{(t)}}L,{\mathrm{\nabla }}_{{\gamma }^{(t)}}L,{\mathrm{\nabla }}_{{\beta }^{(t)}}L$
       更新第$t$层的参数

$$\begin{gathered} W^{(t)}\leftarrow W^{(t)}-\eta {\mathrm{\nabla }}_{W^{(t)}}L \\ {b}^{(t)}\leftarrow b^{(t)}-\eta {\mathrm{\nabla }}_{b^{(t)}}L \\ {\gamma }^{(t)}\leftarrow {\gamma }^{(t)}-\eta {\mathrm{\nabla }}_{{\gamma }^{(t)}}L \\ {\beta }^{(t)}\leftarrow {\beta }^{(t)}-\eta {\mathrm{\nabla }}_{{\beta }^{(t)}}L \end{gathered}$$

    If ($t>1$) {
      将第$t$层的参数误差传递到第$t-1$层

$${\delta }_j^{(t-1)}=\frac{\partial a}{\partial {\tilde{z}}_j^{(t-1)}}\cdot \frac{\partial {\tilde{z}}_j^{(t-1)}}{\partial z_j^{(t-1)}}\cdot W^{(t)}\cdot {\delta }_j^{(t)}$$

    }
  }
}
4. 返回更新的参数向量

习题23.7

  验证逆暂退法和暂退法的等价性。

解答：

解答思路：

1. 写出暂退法（dropout）计算公式
2. 写出逆暂退法（inverted dropout）计算公式
3. 证明两者等价

解答步骤：

第1步: 写出暂退法（dropout）计算公式

  根据书中第23.3.3节的暂退法的描述：

  假设某一隐层的输出向量是 $\mathit{h}$，误差向量是 $\mathit{\delta }$，该层神经元保留与退出的结果用随机向量 $\mathit{d}$ 表示，其中 $\mathit{d}\in \{0,1{\}}^m$ 是维度为 $m$ 的 $0-1$ 向量，1表示对应的神经元保留，0表示对应的神经元退出。那么，在反向传播算法的每一步，经过保留与退出随机判断后，该层的向量表示变为

$$\begin{array}{}\text{(23.69)}& \tilde{\mathit{h}}=\mathit{d}\odot \mathit{h}\end{array}$$$$\begin{array}{}\text{(23.70)}& \tilde{\mathit{\delta }}=\mathit{d}\odot \mathit{\delta }\end{array}$$

这里 $\odot$ 表示逐元素积，使用 $\tilde{\mathit{h}}$ 进行正向传播和使用 $\tilde{\mathit{\delta }}$ 进行反向传播。注意暂退法中每一步的 $\mathit{d}$ 是随机决定的，各步之间并不相同。
  预测时，对隐层的输出向量进行调整：

$$\begin{array}{}\text{(23.71)}& \tilde{\mathit{h}}=p\cdot \mathit{h}\end{array}$$

其中，$p$ 是这层的保留概率。

  由上述可知，暂退法训练时的计算公式：

$$\tilde{\mathit{h}}=\mathit{d}\odot \mathit{h}$$

预测时的计算公式：

$$\tilde{\mathit{h}}=p\cdot \mathit{h}$$

第2步: 写出逆暂退法（inverted dropout）计算公式

  根据书中第23.3.3节的逆暂退法的描述：

  为了方便暂退法的实现，常常采用以下等价的逆暂退法。训练时，将隐层的输出变量放大${\displaystyle \frac{1}{p}}$ 倍：

$$\begin{array}{}\text{(23.72)}& \tilde{\mathit{h}}=\frac{1}{p}\cdot \mathit{d}\odot \mathit{h}\end{array}$$

预测时，隐层的输出权重保持不变。

  由上述可知，逆暂退法训练时计算公式：

$$\tilde{\mathit{h}}=\frac{1}{p}\cdot \mathit{d}\odot \mathit{h}$$

预测时，隐层的输出权重保持不变，可得：

$$\tilde{\mathit{h}}=\mathit{h}$$

第3步: 证明两者等价

  假设不考虑神经元的保留或丢弃时，隐层的输出为

$$y=a(W^{T}x+b)$$

其中$a$为激活函数，$W$为权重参数，$b$为偏置参数。

  假设某一隐层，使用暂退法训练得到的隐层输出向量为${\mathit{h}}_{\text{drop}}$，逆暂退法训练得到的隐层输出向量为${\mathit{h}}_{\text{inv}}$。

  根据暂退法训练时的计算公式，暂退法训练时的输出期望为

$$E[{\tilde{\mathit{h}}}_{\text{drop}}]=E[\mathit{d}\odot {\mathit{h}}_{\text{drop}}]$$

其中 $d$ 表示该层神经元保留与退出的结果，$d$ 为1的概率为 $p$，$p$ 即保留概率，为0的概率为 $1-p$。$d$ 符合伯努利分布，所以：

$$\begin{array}{rl}E[{\tilde{\mathit{h}}}_{\text{drop}}]& =p\cdot {\mathit{h}}_{\text{drop}}+(1-p)\cdot 0\\ & =p\cdot {\mathit{h}}_{\text{drop}}\end{array}$$

由于同一任务的神经网络训练的期望相同，即$E[{\tilde{\mathit{h}}}_{\text{drop}}]=y$，所以：

$$y=p\cdot {\mathit{h}}_{\text{drop}}$$

即：

$${\mathit{h}}_{\text{drop}}=\frac{1}{p}\cdot y$$

根据暂退法预测时计算公式，预测时的隐层输出$y_{\text{drop}}$为：

$$\begin{array}{rl}{y}_{\text{drop}}& =p\cdot {\mathit{h}}_{\text{drop}}\\ & =p\cdot \frac{1}{p}\cdot y\\ & =y\end{array}$$

  根据逆暂退法训练时的计算公式，逆暂退法训练时的输出期望为：

$$E[{\tilde{\mathit{h}}}_{\text{inv}}]=E[\frac{1}{p}\cdot \mathit{d}\odot {\mathit{h}}_{\text{inv}}]$$

$d$同样符合伯努利分布，所以：

$$\begin{array}{rl}E[{\tilde{\mathit{h}}}_{\text{inv}}]& =\frac{1}{p}\cdot p\cdot {\mathit{h}}_{\text{inv}}+\frac{1}{p}\cdot (1-p)\cdot 0\\ & =\frac{1}{p}\cdot p\cdot {\mathit{h}}_{\text{inv}}\\ & ={\mathit{h}}_{\text{inv}}\end{array}$$

由于同一任务的神经网络训练的期望相同，即$E[{\tilde{\mathit{h}}}_{\text{inv}}]=y$，所以：

$$y={\mathit{h}}_{\text{inv}}$$

  根据逆暂退法预测时计算公式，预测时的隐层输出$y_{\text{inv}}$为：

$$\begin{array}{rl}{y}_{\text{inv}}& ={\mathit{h}}_{\text{inv}}\\ & =y\end{array}$$

由于暂退法和逆暂退法预测时的隐层输出相同，所以暂退法与逆暂退法是等价的。