第28章 生成对抗网络

习题28.1

  GAN的生成网络的学习可以定义为以下的最小化问题：

$$\underset{\theta }{min}\{E_{\mathit{z}\sim P_{\text{seed }}(\mathit{z})}[\log (1-D(G(\mathit{z};\mathit{\theta });\overline{\mathit{\phi }}))-\log (D(G(\mathit{z};\mathit{\theta });\overline{\mathit{\phi }}))]\}$$

比较与式（28.2）的不同，并考虑其作用。

解答：

解答思路：

1. 给出式(28.2)定义的生成网络学习的最小化目标函数
2. 比较题中公式和式(28.2)定义的生成网络学习的最小化目标函数函数
3. 分析题中的最小化问题的目标函数的作用

解答步骤：

第1步：给出式(28.2)定义的生成网络学习的最小化目标函数

  根据书中第28.1.1节的公式(28.2)：

  假设已给训练数据$\mathcal{D}$遵循分布$P_{\text{data}}(\mathit{x})$，其中$\mathit{x}$是样本。生成网络用 $\mathit{x}=G(\mathit{z};\mathit{\theta })$表示，其中$\mathit{z}$是输入向量（种子），$\mathit{x}$ 是输出向量（生成数据），$\mathit{\theta }$是网络参数。判别网络是一个二类分类器，用$P(1|\mathit{x})=D(\mathit{x};\mathit{\theta })$表示，其中$\mathit{x}$是输入向量，$P(1|\mathit{x})$和$1-P(1|\mathit{x})$是输出概率，分别白哦是输入$\mathit{x}$来自训练数据和生成数据的概率，$\phi$是网络参数。种子$z$遵循分布$P_{\text{seed}}(\mathit{z})$，生成网络生成的数据分布表示为$P_{\text{gen}}(\mathit{x})$，由$P_{\text{seed}}(\mathit{z})$和$\mathit{x}=G(\mathit{z};\mathit{\theta })$决定。
  如果判别网络参数 $\phi$ 固定，可以通过最小化以下目标函数学习生成网络参数θ。

$$\begin{array}{}\text{(28.2)}& \underset{\theta }{min}\{E_{\mathit{z}\sim P_{\text{seed }}(\mathit{z})}[\log (1-D(G(\mathit{z};\mathit{\theta });\overline{\phi }))\}\end{array}$$

第2步：比较题中公式和式(28.2)定义的生成网络学习的最小化目标函数

  题中GAN的生成网络的学习可以定义为以下的最小化问题：

$$\underset{\theta }{min}\{E_{\mathit{z}\sim P_{\text{seed }}(\mathit{z})}[\log (1-D(G(\mathit{z};\mathit{\theta });\overline{\mathit{\phi }}))-\log (D(G(\mathit{z};\mathit{\theta });\overline{\mathit{\phi }}))]\}$$

与式（28.2）比较，式中多减去了一项：

$$\underset{\theta }{min}\{E_{\mathit{z}\sim P_{\text{seed}}(\mathit{z})}[\log (D(G(\mathit{z};\mathit{\theta });\overline{\mathit{\phi }}))\}$$

第3步：分析题中的最小化问题的目标函数的作用

  令$x=D(G(\mathit{z};\mathit{\theta });\overline{\mathit{\phi }})$，则最小化问题可表示为

$$\underset{\theta }{min}\{E_{\mathit{z}\sim P_{\text{seed }}(\mathit{z})}[\log (1-x)-\log x]\}$$

  题中最小化问题的目标函数的作用：

1. 加速目标函数优化过程的收敛速度：对于$\log (1-x)-\log x$，其求导结果为${\displaystyle -\frac{1}{(1-x)x}}$，可以有效防止$x$取值时导致的梯度减小而难以训练的情况。
2. 防止出现在学习的初始情况，由于生成网络较弱，判别网络很容易区分生成数据和判别数据，导致生成网络的学习难以进行下去的情况。

习题28.2

  两个人进行零和博弈，参与人$X$和$Y$可选择的策略分别是$\mathcal{X}=\{1,2\}$ 和 $\mathcal{Y}=\{1,2\}$。在博弈中，若参与人$X$和$Y$分别选择$i\in \mathcal{X}$和$j\in \mathcal{Y}$，则$X$的损失或$Y$的收益是$a_{ij}$。整体由矩阵$A=(a_{ij})$表示，矩阵$A$定义为:

$$A=\left[\begin{array}{cc}-1& 2\\ 4& 1\end{array}\right]$$

针对这个博弈求 $\underset{i}{min}\underset{j}{max}{a}_{ij}$和$\underset{j}{max}\underset{i}{min}{a}_{ij}$，并验证这时$\underset{j}{max}\underset{i}{min}{a}_{ij}⩽\underset{i}{min}\underset{j}{max}{a}_{ij}$成立。

解答：

解答思路：

1. 给出零和博弈的概念
2. 结合零和博弈的概念，给出题中的求解方法
3. 自编程对该博弈进行求解
4. 验证这时$\underset{j}{max}\underset{i}{min}{a}_{ij}$和$\underset{i}{min}\underset{j}{max}{a}_{ij}$的关系

解答步骤：

第1步：零和博弈的概念

  根据维基百科中的零和博弈
（参考资料：https://zh.wikipedia.org/wiki/零和博弈 ）

  零和博弈，又称零和游戏或零和赛局（Zero-sum game）与非零和博弈相对，是博弈论的一个概念，属非合作博弈。零和博弈表示所有博弈方的利益之和为零或一个常数，即一方有所得，其他方必有所失。在零和博弈中，博弈各方是不合作的。

第2步：结合零和博弈的概念，给出题中的求解方法

  结合第1步给出的零和博弈概念，该博弈的收益矩阵为：

$$A=\left[\begin{array}{cc}-1& 2\\ 4& 1\end{array}\right]$$

  考虑最小最大化原则，即如果参与人$X$先选择策略，此时参与人$X$会选择使自己最小收益最大化的策略，即对应$\underset{j}{max}\underset{i}{min}{a}_{ij}$。
  而对应计算过程，则是先按行计算每一行最小值，然后在每一行的最小值中选择最大值，得到$\underset{j}{max}\underset{i}{min}{a}_{ij}$。

  考虑最大最小化原则，即如果参与人$Y$先选择策略，此时参与人$Y$会选择使对方最大收益最小化的策略，即对应$\underset{i}{min}\underset{j}{max}{a}_{ij}$。
  而对应计算过程，则是先按列计算每一行最大值，然后在每一行的最大值中选择最小值，得到$\underset{i}{min}\underset{j}{max}{a}_{ij}$。

第3步：自编程对该博弈进行求解

import numpy as np

def minmax_function(A):
    """
    从收益矩阵中计算minmax的算法
    :param A: 收益矩阵
    :return: 计算得到的minmax结果
    """
    index_max = []
    for i in range(len(A)):
        # 计算每一行的最大值
        index_max.append(A[i,:].max())
    
    # 计算每一行的最大值中的最小值
    minmax = min(index_max)
    return minmax

def maxmin_function(A):
    """
    从收益矩阵中计算maxmin的算法
    :param A: 收益矩阵
    :return: 计算得到的maxmin结果
    """
    column_min = []
    for i in range(len(A)):
        # 计算每一列的最小值
        column_min.append(A[:,i].min())
        
    # 计算每一列的最小值中的最大值
    maxmin = max(column_min)
    return maxmin

# 创建收益矩阵
A = np.array([[-1,2],[4,1]])
# 计算maxmin
maxmin = maxmin_function(A)
# 计算minmax
minmax = minmax_function(A)
# 输出结果
print("maxmin =", maxmin)
print("minmax =", minmax)

maxmin = 1
minmax = 2

第4步：验证这时$\underset{j}{max}\underset{i}{min}{a}_{ij}$和$\underset{i}{min}\underset{j}{max}{a}_{ij}$的关系

  由上步可得：

$$\begin{gathered} \underset{j}{max}\underset{i}{min}{a}_{ij}=1 \\ \underset{i}{min}\underset{j}{max}{a}_{ij}=2 \end{gathered}$$

这时$\underset{j}{max}\underset{i}{min}{a}_{ij}⩽\underset{i}{min}\underset{j}{max}{a}_{ij}$成立。

习题28.3

  计算以下两个概率分布的Jessen-Shannon散度，设$0log0=0$。

0.1	0.7	0.1	0.1	0
0.2	0	0	0.8	0

解答：

解答思路：

1. 给出Jessen-Shannon散度的定义
2. 写出题中数据的Jessen-Shannon散度数值计算过程
3. 使用自编程实现并验证计算结果

解答步骤：

第1步：Jessen-Shannon散度的定义

  根据维基百科的Jessen-Shannon散度
（参考Wiki：https://en.wikipedia.org/wiki/Jensen–Shannon_divergence ）

给出两个概率分布$P$和$Q$，其Jessen-Shannon散度为：

$$\text{JS}(P\parallel Q)=\frac{1}{2}D(P\parallel M)+\frac{1}{2}D(Q\parallel M)$$

其中${\displaystyle M=\frac{1}{2}(P+Q)}$，$D(\cdot \parallel \cdot )$表示为KL散度。

  根据书中附录E的KL散度的定义：

KL散度是描述两个概率分布$Q(x)$和$P(x)$相似度的一种度量，记作$D(Q\parallel P)$。对离散随机变量，KL散度定义为

$$D(Q\parallel P)=\sum _{i}Q(i)\log \frac{Q(i)}{P(i)}$$

对连续随机变量，KL散度定义为

$$D(P\parallel Q)=\int Q(x)\log \frac{Q(x)}{P(x)}\text{d}x$$

第2步：写出题中数据的Jessen-Shannon散度数值计算过程

  由于题中数据是离散值，采用对离散随机变量的KL散度公式进行计算，得到：

$$\begin{gathered} P=[0.1,0.7,0.1,0.1,0] \\ Q=[0.2,0,0,0.8,0] \\ M=\frac{1}{2}(P+Q)=[0.15,0.35,0.05,0.45,0] \end{gathered}$$

  则对应KL散度为：

$$\begin{gathered} D(P\parallel M)=\sum _{i}P(i)\ln \frac{P(i)}{M(i)}=\ln 2-0.3\ast \ln 3 \\ D(Q\parallel M)=\sum _{i}Q(i)\ln \frac{Q(i)}{M(i)}=3.6\ast \ln 2-1.8\ast \ln 3 \end{gathered}$$

计算JS散度，得到：

$$\begin{array}{rl}\text{JS}(P\parallel Q)& =\frac{1}{2}D(P\parallel M)+\frac{1}{2}D(Q\parallel M)\\ & =\frac{1}{2}(4.6\ast \ln 2-2.1\ast \ln 3)\\ & =2.3\ast \ln 2-1.05\ast \ln 3\\ & =0.440696\end{array}$$

第3步：使用自编程实现并计算结果

  通过调用scipy.stats的entropy函数，根据题目中的两个概率分布进行计算，得到两个分布的Jessen-Shannon散度。

from scipy.stats import entropy
import numpy as np

# 加载数据
P = [0.1, 0.7, 0.1, 0.1, 0]
Q = [0.2, 0, 0, 0.8, 0]

# 计算z=(x+y)/2
M =[(P[i] + Q[i]) / 2 for i in range(min(len(P),len(Q)))]

# 计算P和M之间的KL散度，Q和M之间的KL散度
DL_P_M = entropy(P, M)
DL_Q_M = entropy(Q, M)

# 计算JS散度
result = (DL_P_M + DL_Q_M) / 2

# 输出结果
print("Jessen-Shannon Distance = {:f}".format(result))

Jessen-Shannon Distance = 0.440696

可得到两个概率分布的Jessen-Shannon散度为0.440696。

习题28.4

  证明两个概率分布 $P$ 和 $Q$ 之间的 Jessen-Shannon 散度满足以下关系，当且仅当 $P$ 和 $Q$ 相同时取最小值 0，设对数是自然对数。

$$0⩽\text{JS}(P\parallel Q)⩽\ln 2$$

解答：

解答思路：

1. 给出两个概率分布$P$和$Q$之间的Jessen-Shannon散度
2. 证明当且仅当$P$和$Q$相同时，Jessen-Shannon散度取最小值0
3. 证明Jessen-Shannon散度取最大值 $\ln 2$（设对数是自然对数）
4. 结合上述证明，得到 $\text{JS}(P\parallel Q)$ 关系式

解答步骤：

第1步：两个概率分布 𝑃 和 𝑄 之间的Jessen-Shannon散度

  根据维基百科的Jessen-Shannon散度
（参考Wiki：https://en.wikipedia.org/wiki/Jensen–Shannon_divergence ）

给出两个概率分布$P$和$Q$，其Jessen-Shannon散度为：

$$\text{JS}(P\parallel Q)=\frac{1}{2}D(P\parallel M)+\frac{1}{2}D(Q\parallel M)$$

其中${\displaystyle M=\frac{1}{2}(P+Q)}$，$D(\cdot \parallel \cdot )$表示为KL散度。

第2步：证明当且仅当 $P$ 和 $Q$ 相同时，Jessen-Shannon散度取最小值0

  首先，将两个概率分布$P$和$Q$的Jessen-Shannon散度展开为Kullback–Leibler散度形式：

$$\text{JS}(P\parallel Q)=\frac{1}{2}D(P\parallel M)+\frac{1}{2}D(Q\parallel M)$$

  根据书中附录E的KL散度的性质：

KL散度具有性质：$ D(P | Q) \geqslant 0$。当且仅当 $Q=P$ 时，$D(P\parallel Q)=0$。

  将上述KL散度的性质带入两个概率分布P和Q的Jessen-Shannon散度展开式可知：当且仅当$P$和$M$相同，且$Q$和$M$相同时，则有

$$\text{JS}(P\parallel Q)=0$$

根据$M$的定义可知，则有

$$P=Q=M=\frac{1}{2}(P+Q)$$

  综上所述，可证得当前仅当$P$和$Q$相同时，Jessen-Shannon散度取最小值0。

第3步：证明Jessen-Shannon散度取最大值 $\ln 2$（设对数是自然对数）

  可知两个概率分布$P$和$Q$的Jessen-Shannon散度可表示为：

$$\text{JS}(P\parallel Q)=\frac{1}{2}D(P\parallel M)+\frac{1}{2}D(Q\parallel M)$$

1. 假设$P$和$Q$是连续型随机变量的概率分布

  将连续随机变量的KL散度公式带入展开，并且将${\displaystyle M=\frac{1}{2}(P+Q)}$代入：

$$\begin{array}{rl}\text{JS}(P\parallel Q)& =\frac{1}{2}\int P(x)\ln \left(\frac{P(x)}{{\displaystyle \frac{P(x)+Q(x)}{2}}}\right)\text{d}x+\frac{1}{2}\int Q(x)\ln \left(\frac{Q(x)}{{\displaystyle \frac{P(x)+Q(x)}{2}}}\right)\text{d}x\\ & =\frac{1}{2}\int P(x)\ln \left(\frac{2P(x)}{P(x)+Q(x)}\right)\text{d}x+\frac{1}{2}\int Q(x)\ln \left(\frac{2Q(x)}{P(x)+Q(x)}\right)\text{d}x\\ & =\frac{1}{2}\int [P(x)\ln \left(\frac{P(x)}{P(x)+Q(x)}\right)+Q(x)\ln \left(\frac{Q(x)}{P(x)+Q(x)}\right)]\text{d}x+\ln 2\end{array}$$

可知：

$$\begin{gathered} \ln \left(\frac{P(x)}{P(x)+Q(x)}\right)⩽0 \\ \ln \left(\frac{Q(x)}{P(x)+Q(x)}\right)⩽0 \end{gathered}$$

可得：

$$\frac{1}{2}\int [P(x)\ln \left(\frac{P(x)}{P(x)+Q(x)}\right)+Q(x)\ln \left(\frac{Q(x)}{P(x)+Q(x)}\right)]\text{d}x⩽0$$

所以：

$$\text{JS}(P\parallel Q)=\frac{1}{2}\int [P(x)\ln \left(\frac{P(x)}{P(x)+Q(x)}\right)+Q(x)\ln \left(\frac{Q(x)}{P(x)+Q(x)}\right)]\text{d}x+\ln 2⩽\ln 2$$

当且仅当概率分布$P$和$Q$完全不重叠时，Jessen-Shannon散度的最大值为$\ln 2$。

2. 假设$P$和$Q$是离散型随机变量的概率分布

  将离散随机变量的KL散度公式带入展开，并且将${\displaystyle M=\frac{1}{2}(P+Q)}$代入：

$$\begin{array}{rl}\text{JS}(P\parallel Q)& =\frac{1}{2}D(P\parallel M)+\frac{1}{2}D(Q\parallel M)\\ & =\frac{1}{2}\sum _{i}P(i)\ln \left(\frac{P(i)}{{\displaystyle \frac{P(i)+Q(i)}{2}}}\right)+\frac{1}{2}\sum _{i}Q(i)\ln \left(\frac{Q(i)}{{\displaystyle \frac{P(i)+Q(i)}{2}}}\right)\\ & =\frac{1}{2}\sum _{i}P(i)\ln \left(\frac{2P(i)}{P(i)+Q(i)}\right)+\frac{1}{2}\sum _{i}Q(i)\ln \left(\frac{2Q(i)}{P(i)+Q(i)}\right)\\ & =\frac{1}{2}\sum _i[P(i)\ln \left(\frac{P(i)}{P(i)+Q(i)}\right)+Q(i)\ln \left(\frac{Q(i)}{P(i)+Q(i)}\right)]+\ln 2\end{array}$$

可知：

$$\begin{gathered} \ln \left(\frac{P(i)}{P(i)+Q(i)}\right)⩽0 \\ \ln \left(\frac{Q(i)}{P(i)+Q(i)}\right)⩽0 \end{gathered}$$

可得：

$$\frac{1}{2}\sum _i[P(i)\ln \left(\frac{P(i)}{P(i)+Q(i)}\right)+Q(i)\ln \left(\frac{Q(i)}{P(i)+Q(i)}\right)]⩽0$$

所以：

$$\text{JS}(P\parallel Q)=\frac{1}{2}\sum _i[P(i)\ln \left(\frac{P(i)}{P(i)+Q(i)}\right)+Q(i)\ln \left(\frac{Q(i)}{P(i)+Q(i)}\right)]+\ln 2⩽\ln 2$$

当且仅当概率分布$P$和$Q$完全不重叠时，Jessen-Shannon散度的最大值为$\ln 2$。

故，可得：

$$\text{JS}(P\parallel Q)⩽\ln 2$$

第4步：结合上述证明，得到 $\text{JS}(P\parallel Q)$ 关系式

  根据第2步和第3步，两个概率分布 $P$ 和 $Q$ 之间的 Jessen-Shannon 散度满足以下关系，当且仅当 $P$ 和 $Q$ 相同时取最小值 0，设对数是自然对数。

$$0⩽\text{JS}(P\parallel Q)⩽\ln 2$$

习题28.5

  考虑一维卷积运算，其输入是5维的向量 $\mathit{x}$，输出是3维向量 $\mathit{z}$。卷积核是 $\mathit{w}=(w_1,w_2,w_3)$，步幅为1，填充为0。写出该卷积运算的矩阵表示，给出对应的转置卷积，并且验证原始卷积核 $\mathit{w}$ 和转置卷积核 ${\mathit{w}}^{\prime }$ 之间有 $\mathit{w}=\text{rot180}({\mathit{w}}^{\prime })$ 成立。

解答：

解答思路：

1. 写出该卷积运算的矩阵表示
2. 写出对应的转置卷积
3. 证明原始卷积核 $\mathit{w}$ 和转置卷积核 ${\mathit{w}}^{\prime }$ 满足 $\mathit{w}=\text{rot180}({\mathit{w}}^{\prime })$

解答步骤：

第1步：写出该卷积运算的矩阵表示

  假设输入的5维向量 $\mathit{x}$ 表示为$[ x_1, x_2, x_3, x_4, x_5 ]^T $，输出的3维向量 $\mathit{z}$ 表示为$[ z_1, z_2, z_3]^T $

  根据书中第28.2.1节的卷积运算的矩阵表示，可构建矩阵$C$：

$$C=\left[\begin{array}{ccccc}{w}_1& w_2& w_3& 0& 0\\ 0& w_1& w_2& w_3& 0\\ 0& 0& w_1& w_2& w_3\end{array}\right]$$

  根据书中第28.2.1节关于矩阵 $C$ 的线性变换描述：

  考虑基于矩阵 $C$ 的线性变换，其输入是输入矩阵展开的向量，输出是输出矩阵展开的向量。这个线性变换对应神经网络前一层道后一层的信号传递（正向传播），而以上卷积运算表示在这个线性变换中。

可得卷积运算的矩阵表示：

$$\left[\begin{array}{ccccc}{w}_1& w_2& w_3& 0& 0\\ 0& w_1& w_2& w_3& 0\\ 0& 0& w_1& w_2& w_3\end{array}\right]\cdot \left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\end{array}\right]=\left[\begin{array}{c}{z}_1\\ z_2\\ z_3\end{array}\right]$$

第2步：写出对应的转置卷积

  根据书中第28.2.1节的转置卷积的描述，可构建矩阵$C^T$

$$C^T=\left[\begin{array}{ccc}{w}_1& 0& 0\\ w_2& w_1& 0\\ w_3& w_2& w_1\\ 0& w_3& w_2\\ 0& 0& w_3\end{array}\right]$$

  根据书中第28.2.1节关于矩阵$C^T$的线性变换描述：

考虑基于转置矩阵$C^T$的线性变换。这个线性变换对应神经网络后一层到前一层的信号传递（反向传播）。

可得对应的转置卷积为

$$\left[\begin{array}{ccc}{w}_1& 0& 0\\ w_2& w_1& 0\\ w_3& w_2& w_1\\ 0& w_3& w_2\\ 0& 0& w_3\end{array}\right]\cdot \left[\begin{array}{c}{z}_1\\ z_2\\ z_3\end{array}\right]=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\end{array}\right]$$

这个转置卷积是核矩阵为${\mathit{w}}^{\prime }=(w_3,w_2,w_1)$、填充为2、步幅为1的卷积运算。

第3步：证明原始卷积核 $\mathit{w}$ 和转置卷积核 ${\mathit{w}}^{\prime }$ 满足 $\mathit{w}=\text{rot180}({\mathit{w}}^{\prime })$

  因为原始卷积核$\mathit{w}=(w_1,w_2,w_3)$，而转置卷积核${\mathit{w}}^{\prime }=(w_3,w_2,w_1)$，可得：

$$\mathit{w}=\text{rot180}({\mathit{w}}^{\prime })$$

习题28.6

  写出图28.8中转置卷积的大小和原始卷积的大小之间的关系，转置卷积有输入矩阵尺寸 ${\hat{I}}^{\prime }$、卷积核尺寸 $K^{\prime }$、步幅 $S^{\prime }$、填充尺寸 $P^{\prime }$、输出矩阵尺寸 $O^{\prime }$。

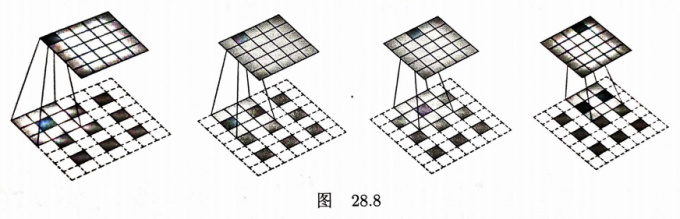
解答：

解答思路：

1. 给出转置卷积的大小计算
2. 写出图中转置卷积的大小
3. 写出图中原始卷积的大小
4. 写出图中转置卷积的大小和原始卷积的大小之间的关系

解答步骤：

第1步：给出转置卷积的大小计算

  根据书中第28.2.1节的转置卷积的大小计算：

首先，计算原始卷积的大小。这里考虑简单的情况。假设输入矩阵是方阵，卷积核矩阵也是方阵。设 $I$ 是输入矩阵的尺寸，$K$ 是卷积核的尺寸，$P$ 是填充的尺寸，$S$ 是步幅。输出矩阵的尺寸 $O$ 满足

$$\begin{array}{}\text{(28.13)}& O=\frac{I+2P-K}{S}+1\end{array}$$

这里考虑可以整除的情况，式（28.13）可以改为对应的形式：

$$I=\frac{[O+(O-1)(S-1)]+2(K-P-1)-K}{1}+1$$

接着，计算转置卷积的大小。设 $I^{\prime }$ 是输入矩阵的尺寸，$K^{\prime }$ 是卷积核的尺寸，$P^{\prime }$ 是填充的尺寸，$S^{\prime }$ 是步幅。输出矩阵的尺寸$O^{\prime }$ 满足

$$O^{\prime }=\frac{I^{\prime }+2P^{\prime }-K^{\prime }}{S^{\prime }}+1$$

这里也考虑可以整除的情况。转置卷积的输出矩阵尺寸 $O^{\prime }$ 与原始卷积的输入矩阵尺寸 $I^{\prime }$ 相同。因此，可以推算，当 $S = 1, P = 0 $时，转置卷积的大小和原始卷积的大小之间有以下关系：

$$\begin{gathered} I^{\prime }=O,P^{\prime }=K-1,K^{\prime }=K,S^{\prime }=1 \\ {O}^{\prime }=O+K-1 \end{gathered}$$

第2步：写出图中转置卷积的大小

  根据图中的信息，转置卷积的输入矩阵（插入0向量后）尺寸为5，卷积核尺寸为3，步幅为1，填充尺寸为1， 输出矩阵尺寸为5，即 ${\hat{I}}^{\prime }=5,K^{\prime }=3,S^{\prime }=1,P^{\prime }=1,O^{\prime }=5$。

第3步：写出图中原始卷积的大小

  根据图中的信息，原始卷积输入矩阵尺寸为5，卷积核尺寸为3，步幅为1，填充尺寸为0，输出矩阵尺寸为3，即 $I=5,K=3,S=1,P=0,O=3$。

第4步：写出图中转置卷积的大小和原始卷积的大小之间的关系

  当 $S=1,P=0$ 时，转置卷积的大小和原始卷积的大小之间有以下关系成立：

$$\begin{gathered} {\hat{I}}^{\prime }=O+(O-1) \\ {P}^{\prime }=K-2 \\ {K}^{\prime }=K \\ {S}^{\prime }=1 \\ {O}^{\prime }=O+K-1 \end{gathered}$$

参考文献

【1】零和博弈（来源于Wiki百科）：https://zh.wikipedia.org/wiki/零和博弈
【2】Jessen-Shannon散度（来源于Wiki百科）：https://en.wikipedia.org/wiki/Jensen–Shannon_divergence