第24章卷积神经网络

习题24.1

  设有输入矩阵$X=[x_{ij}{]}_{I\times J}$，核矩阵$W=[w_{mn}{]}_{M\times N}$，满足$M\ll I,N\ll J$，则称以下运算为二维数学卷积：

$$Y=W⊛X$$

产生输出矩阵$Y=[y_{kl}{]}_{K\times L}$，其中

$$\begin{gathered} y_{kl}=\sum _{m=1}^M\sum _{n=1}^N{w}_{mn}{x}_{i-m+1,j-n+1} \\ K=I-M+1,L=J-N+1 \end{gathered}$$

证明数学卷积和机器学习卷积有以下关系：

$$W⊛X=\text{rot180}(W)\ast X$$

这里$⊛$表示数学卷积，$\ast$表示机器学习卷积，rot180()表示对矩阵的180度旋转。

解答：

解答思路：

1. 给出机器学习二维卷积的定义
2. 计算$\text{rot180}(W)\ast X$输出矩阵$Y^{\prime }$
3. 验证$Y$与$Y^{\prime }$相等

解答步骤：

第1步：给出机器学习二维卷积的定义

  根据书中第24.1.2节的定义24.1的二维卷积的定义：

定义24.1（二维卷积） 给定一个 $I\times J$ 输入矩阵 $X=[x_{i,j}{]}_{I\times J}$，一个 $M\times N$ 核矩阵 $W=[w_{m,n}{]}_{M\times N}$，满足 $M\ll I,N\ll J$。让核矩阵在输入矩阵上从左到右再从上到下按顺序滑动，在滑动的每一个位置，核矩阵与输入矩阵的一个子矩阵重叠。求核矩阵与每一个子矩阵的内积，产生一个 $K\times L$ 输出矩阵 $Y=[y_{k,l}{]}_{K\times L}$，称此运算为卷积（convolution）或二维卷积。写作

$$\begin{array}{}\text{(24.4)}& Y=W\ast X\end{array}$$

其中, $Y=[y_{k,l}{]}_{K\times L}$。

$$\begin{array}{}\text{(24.5)}& y_{k,l}=\sum _{m=1}^M\sum _{n=1}^N{w}_{m,n}{x}_{k+m-1,l+n-1}\end{array}$$

其中，$k=1,2,\cdots ,K,l=1,2,\cdots ,L,K=I-M+1,L=J-N+1$。

第2步：计算$\text{rot180}(W)\ast X$输出矩阵$Y^{\prime }$

  令$W^{\prime }=\text{rot180}(W)=[w_{m,n}^{\prime }{]}_{M\times N}=[w_{M-m+1,N-n+1}{]}_{M\times N}$，则对于$\text{rot180}(W)\ast X$输出矩阵$Y^{\prime }=[y_{k,l}^{\prime }{]}_{K\times L}$有：

$$\begin{array}{rl}{y}_{k,l}^{\prime }& =\sum _{m=1}^M\sum _{n=1}^N{w}_{m,n}^{\prime }{x}_{k+m-1,l+n-1}\\ & =\sum _{m=1}^M\sum _{n=1}^N{w}_{M-m+1,N-n+1}{x}_{k+m-1,l+n-1}\end{array}$$

  令$p=M-m+1$，且当$m=1$时，$p=M$，当$m=M$时，$p=1$；令$q=N-n+1$，且当$n=1$，$q=N$，当$n=N$，$q=1$，则：

$$\begin{array}{rl}{y}_{k,l}^{\prime }& =\sum _{p=M}^1\sum _{q=N}^1{w}_{p,q}{x}_{k+M-p,l+N-q}\\ & =\sum _{p=1}^M\sum _{q=1}^N{w}_{p,q}{x}_{k+M-p,l+N-q}\end{array}$$

第3步：验证$Y$与$Y^{\prime }$相等

  对于$Y=W⊛X=[y_{kl}{]}_{K\times L}$，由题目可知：

$$\begin{gathered} y_{k,l}=\sum _{m=1}^M\sum _{n=1}^N{w}_{m,n}{x}_{i-m+1,j-n+1} \\ K=I-M+1,L=J-N+1 \end{gathered}$$

可令$i=k+M-1,j=l+N-1$，则

$$\begin{gathered} i-m+1=k+M-m \\ j-n+1=l+N-n \end{gathered}$$

可得：

$$y_{k,l}=\sum _{m=1}^M\sum _{n=1}^N{w}_{mn}{x}_{k+M-m,l+N-n}$$

  因此，$W⊛X=Y=Y^{\prime }=\text{rot180}(W)\ast X$，故原命题得证。

习题24.2

  假设有矩阵

$$A=\left[\begin{array}{cccc}3& 2& 0& 1\\ 0& 2& 1& 2\\ 2& 0& 0& 3\\ 2& 3& 1& 2\end{array}\right],B=\left[\begin{array}{ccc}2& 1& 2\\ 0& 0& 3\\ 0& 0& 2\end{array}\right]$$

其中，$A$是输入矩阵，$B$是核矩阵，可以求得数学卷积$B⊛A$是

$$B⊛A=\left[\begin{array}{cccccc}6& 7& 8& 6& 1& 3\\ 0& 4& 13& 15& 4& 7\\ 4& 2& 10& 16& 6& 14\\ 4& 8& 15& 15& 6& 17\\ 0& 0& 10& 9& 3& 12\\ 0& 0& 4& 6& 2& 4\end{array}\right]$$

试求数学卷积$A⊛B$，并验证数学卷积满足交换律。

解答：

解答思路：

1. 给出数学卷积的定义
2. 给出二维数学卷积的定义
3. 计算数学卷积$A⊛B$
4. 验证数学卷积满足交换律

解答步骤：

第1步：数学卷积的定义

  根据书中第24.1.2节的数学卷积的定义：

  在数学中，卷积（convolution）是定义在两个函数上的运算，表示用其中一个函数对另一个函数的形状进行的调整。这里考虑一维卷积。设 $f$ 和 $g$ 是两个可积的实值函数，则积分

$${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}f(\tau )g(t-\tau )\text{d}\tau$$

  定义了一个新的函数 $h(t)$，称为 $f$ 和 $g$ 的卷积，记作

$$h(t)=(f⊛g)(t)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}f(\tau )g(t-\tau )\text{d}\tau$$

其中，符号 $⊛$ 表示卷积运算。

第2步：二维数学卷积的定义

  见习题24.1中二维数学卷积：

$$Y=W⊛X$$

其中输入矩阵$X=[x_{ij}{]}_{I\times J}$，核矩阵$W=[w_{mn}{]}_{M\times N}$，满足$M\ll I,N\ll J$，产生输出矩阵$Y=[y_{kl}{]}_{K\times L}$，其中

$$\begin{gathered} y_{kl}=\sum _{m=1}^M\sum _{n=1}^N{w}_{mn}{x}_{i-m+1,j-n+1} \\ K=I-M+1,L=J-N+1 \end{gathered}$$

第3步：计算数学卷积$A⊛B$

  根据定义，计算$A⊛B$

$$A⊛B=\left[\begin{array}{cccccc}6& 7& 8& 6& 1& 3\\ 0& 4& 13& 15& 4& 7\\ 4& 2& 10& 16& 6& 14\\ 4& 8& 15& 15& 6& 17\\ 0& 0& 10& 9& 3& 12\\ 0& 0& 4& 6& 2& 4\end{array}\right]$$

第4步：验证数学卷积满足交换律

  不妨设

$$h^{\prime }(t)=(g⊛f)(t)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}g(\tau )f(t-\tau )\mathrm{d}\tau$$

  令 $t-\tau =\lambda$，$\mathrm{d}\lambda =-\mathrm{d}\tau$，且当$\tau \to +\mathrm{\infty }$时，$\lambda \to -\mathrm{\infty }$；当$\tau \to -\mathrm{\infty }$时，$\lambda \to +\mathrm{\infty }$，则：

$$\begin{array}{rl}{h}^{\prime }(t)& =-{\int }_{+\mathrm{\infty }}^{-\mathrm{\infty }}g(t-\lambda )f(\lambda )\mathrm{d}\lambda \\ & ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}g(t-\lambda )f(\lambda )\mathrm{d}\lambda \end{array}$$

  因此，$(g⊛f)(t)=(f⊛g)(t)$，即数学卷积满足交换律，原命题得证。

习题24.3

  验证机器学习卷积（互相关）不满足交换律。

解答：

解答思路：

1. 给出机器学习卷积定义
2. 计算$X\ast W$
3. 验证$X\ast W$与$W\ast X$不相等

解答步骤：

第1步：机器学习卷积定义

  根据书中第24章的本章概要的机器学习卷积的定义：

给定输入矩阵$X=[x_{ij}{]}_{I\times J}$，核矩阵$W=[w_{mn}{]}_{M\times N}$。让核矩阵在输入矩阵上按顺序滑动，（二维）卷积是定义在核矩阵与输入矩阵的子矩阵的内积，产生输出矩阵$Y=[y_{kl}{]}_{K\times L}$。

$$Y=W\ast X$$

其中，$Y=[y_{kl}{]}_{K\times L}$，${\displaystyle y_{kl}=\sum _{m=1}^M\sum _{n=1}^N{w}_{m,n}{x}_{k+m-1,l+n-1}}$。

第2步：计算$X\ast W$

  设$X\ast W$的输出矩阵为$Y^{\prime }=[y_{kl}^{\prime }{]}_{K^{\prime }\times L^{\prime }}$，则

$$y_{kl}^{\prime }=\sum _{i=1}^I\sum _{j=1}^J{x}_{i,j}{w}_{k+i-1,l+j-1}$$

其中$k=1,2,\cdots ,K^{\prime },l=1,2,\cdots ,L^{\prime },K^{\prime }=M-I+1,L^{\prime }=N-J+1$。

  令$p=k+i-1$，当$i=1$时，$p=k$，当$i=I$时，$p=k+I-1$；令$q=l+j-1$，当$j=1$，$q=l$，当$j=J$，$q=l+J-1$，则

$$y_{kl}^{\prime }=\sum _{p=k}^{k+I-1}\sum _{q=l}^{l+J-1}{w}_{p,q}{x}_{p-k+1,q-l+1}$$

第3步：验证$X\ast W$与$W\ast X$不相等

  综上，$Y^{\prime }=[y_{kl}^{\prime }{]}_{K^{\prime }\times L^{\prime }}\ne Y=[y_{kl}{]}_{K\times L}$，即 $X\ast W\ne W\ast X$，原命题得证。

习题24.4

  CNN也可以用于一维数据的处理，求图24.22所示的一维卷积。

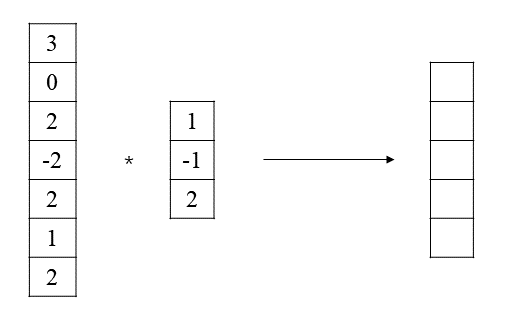
解答：

解答思路：

1. 根据二维卷积的定义，写出一维卷积的定义
2. 计算一维卷积的输出矩阵

解答步骤：

第1步：根据二维卷积的定义，写出一维卷积的定义

  给定一个$I\times 1$输入矩阵$X$和$M\times 1$核矩阵$W$，可将它们视作第2维度为1的二维矩阵，则产生的输出矩阵为

$$Y=W\ast X=[y_{k,1}{]}_{K\times 1}$$

其中

$$y_{k,1}=\sum _{m=1}^M{w}_{m,1}{x}_{k+m-1,1}$$

其中，$k=1,2,\cdots ,K,K=I-M+1$。

第2步：计算一维卷积的输出矩阵

  根据上述公式计算可得：

$$\begin{array}{rl}{y}_{1,1}& =\sum _{m=1}^3{w}_{m,1}{x}_{1+m-1,1}=3\times 1+0\times -1+2\times 2=7\\ y_{2,1}& =\sum _{m=1}^3{w}_{m,1}{x}_{2+m-1,1}=0\times 1+2\times -1+-2\times 2=-6\\ y_{3,1}& =\sum _{m=1}^3{w}_{m,1}{x}_{3+m-1,1}=2\times 1+-2\times -1+2\times 2=8\\ y_{4,1}& =\sum _{m=1}^3{w}_{m,1}{x}_{4+m-1,1}=-2\times 1+2\times -1+1\times 2=-2\\ y_{5,1}& =\sum _{m=1}^3{w}_{m,1}{x}_{5+m-1,1}=2\times 1+1\times -1+2\times 2=5\end{array}$$

  一维卷积的输出矩阵为

$$Y=\left[\begin{array}{c}7\\ -6\\ 8\\ -2\\ 5\end{array}\right]$$

习题24.5

  通过例24.2验证卷积运算不具有旋转可变性。假设对图像数据进行90度顺时针和逆时针旋转。

解答：

解答思路：

1. 将输入矩阵$X$顺时针旋转90度，计算卷积核为$W$时的输出矩阵
2. 将输入矩阵$X$逆时针旋转90度，计算卷积核为$W$时的输出矩阵
3. 验证旋转之后产生的输出矩阵与未旋转产生的输出矩阵不相等

解答步骤：

  例24.2给定的输入矩阵$X$和核矩阵$W$：

$$X=\left[\begin{array}{cccc}3& 2& 0& 1\\ 0& 2& 1& 2\\ 2& 0& 0& 3\\ 2& 3& 1& 2\end{array}\right],W=\left[\begin{array}{ccc}2& 1& 2\\ 0& 0& 3\\ 0& 0& 2\end{array}\right]$$

第1步：将输入矩阵$X$顺时针旋转90度，计算卷积核为$W$时的输出矩阵

  将输入矩阵$X$顺时针旋转90度，得：

$$X_{rot90}=\text{rot90}(X)=\left[\begin{array}{cccc}2& 2& 0& 3\\ 3& 0& 2& 2\\ 1& 0& 1& 0\\ 2& 3& 2& 1\end{array}\right]$$

  根据二维卷积定义，得到输出矩阵

$$Y_{rot90}=W\ast X_{rot90}=\left[\begin{array}{ccc}2& 1& 2\\ 0& 0& 3\\ 0& 0& 2\end{array}\right]\ast \left[\begin{array}{cccc}2& 2& 0& 3\\ 3& 0& 2& 2\\ 1& 0& 1& 0\\ 2& 3& 2& 1\end{array}\right]=\left[\begin{array}{cc}14& 16\\ 17& 8\end{array}\right]$$

第2步：将输入矩阵$X$逆时针旋转90度，计算卷积核为$W$时的输出矩阵

  将输入矩阵$X$逆时针旋转90度，得：

$$X_{rot-90}=\text{rot-90}(X)=\left[\begin{array}{cccc}1& 2& 3& 2\\ 0& 1& 0& 1\\ 2& 2& 0& 3\\ 3& 0& 2& 2\end{array}\right]$$

  根据二维卷积定义，得到输出矩阵：

$$Y_{rot-90}=W\ast X_{rot-90}=\left[\begin{array}{ccc}2& 1& 2\\ 0& 0& 3\\ 0& 0& 2\end{array}\right]\ast \left[\begin{array}{cccc}1& 2& 3& 2\\ 0& 1& 0& 1\\ 2& 2& 0& 3\\ 3& 0& 2& 2\end{array}\right]=\left[\begin{array}{cc}10& 20\\ 5& 17\end{array}\right]$$

第3步：验证旋转之后产生的输出矩阵与未旋转产生的输出矩阵不相等

  由例24.2可知，

$$Y=W\ast X=\left[\begin{array}{ccc}2& 1& 2\\ 0& 0& 3\\ 0& 0& 2\end{array}\right]\ast \left[\begin{array}{cccc}3& 2& 0& 1\\ 0& 2& 1& 2\\ 2& 0& 0& 3\\ 2& 3& 1& 2\end{array}\right]=\left[\begin{array}{cc}11& 18\\ 6& 22\end{array}\right]$$

  显然，$Y\ne Y_{rot90}\ne Y_{rot-90}$，即卷积运算不具有旋转可变性。

习题24.6

  证明感受野的关系式（24.19）成立。

解答：

解答思路：

1. 给出感受野的关系式
2. 写出感受野递推形式的计算公式
3. 用数学归纳法证明感受野关系式成立

解答步骤：

第1步：感受野的关系式

  根据书中第24.1.4节的感受野的关系式：

  考虑卷积神经网络全部由卷积层组成的情况，神经元的感受野的大小有以下关系成立。

$$\begin{array}{}\text{(24.19)}& R^{(l)}=1+\sum _{j=1}^l(F^{(j)}-1)\prod _{i=0}^{j-1}{S}^{(i)}\end{array}$$

设输入矩阵和卷积核都呈正方形。$R^{(l)}\times R^{(l)}$ 表示第 $l$ 层的神经元的感受野的大小，$F^{(j)}\times F^{(j)}$ 表示第 $j$ 层的卷积核的大小，$S^{(i)}$ 表示第 $i$ 层卷积的步幅，设 $S^{(0)}=1$。

第2步：写出感受野递推形式的计算公式

  每个卷积层的每个神经元只与上一层的一部分神经元相连，故我们可根据上一层卷积层情况推导出下一层的感受野，感受野递推形式的计算公式如下：

$$R^{(l)}=R^{(l-1)}+(F^{(l)}-1)I^{(l)}$$

其中，$R^{(l)}\times R^{(l)}$和$R^{(l-1)}\times R^{(l-1)}$分别表示第$l$和$l-1$层的神经元的感受野的大小，$F^{(j)}\times F^{(j)}$ 表示第 $j$ 层的卷积核的大小。$I^{(l)}$表示第$l$层输出特征图的特征间的间隔，由$I^{(l)}=I^{(l-1)}\cdot S^{l-1}$，设$I^{(0)}=1$。

第3步：用数学归纳法证明感受野关系式成立

  当$l=1$时，$R^1=1+(F^1-1)=F^1$，显然成立

  假设当 $l=n$ 时，

$$R^{(n)}=1+\sum _{j=1}^n(F^{(j)}-1)\prod _{i=0}^{j-1}{S}^{(i)}$$

  成立。

  当$l=n+1$时，

$$\begin{array}{rl}{R}^{(n+1)}& =R^{(n)}+(F^{(n+1)}-1)I^{n+1}\\ & =R^{(n)}+(F^{(n+1)}-1)I^n{S}^n\\ & =R^{(n)}+(F^{(n+1)}-1)I^{n-1}{S}^{n-1}{S}^n\\ & =R^{(n)}+(F^{(n+1)}-1)I^0{S}^0{S}^1\cdots S^{n-1}{S}^n\\ & =R^{(n)}+(F^{(n+1)}-1)\prod _{i=0}^n{S}^{(i)}\\ & =1+\sum _{j=1}^n(F^{(j)}-1)\prod _{i=0}^{j-1}{S}^{(i)}+(F^{(n+1)}-1)\prod _{i=0}^n{S}^{(i)}\\ & =1+\sum _{j=1}^{n+1}(F^{(j)}-1)\prod _{i=0}^{j-1}{S}^{(i)}\end{array}$$

结合$R^{(n)}$和$R^{(n+1)}$的关系式，可得到：

$$R^{(l)}=1+\sum _{j=1}^l(F^{(j)}-1)\prod _{i=0}^{j-1}{S}^{(i)}$$

习题24.7

  设计一个基于CNN的自然语言句子分类模型。假设句子是单词序列，每个单词用一个实数向量表示。

解答：

解答思路：

1. 给出自然语言句子分类模型的参考文献和相关的模型架构图
2. 使用PyTorch编程实现模型

解答步骤：

第1步：给出自然语言句子分类模型的参考文献和相关的模型架构图

  根据Chen,Yahui的Convolutional neural network for sentence classification. MS thesis. University of Waterloo论文，该论文提出了一种基于CNN的自然语言句子分类模型，其模型架构图如下：

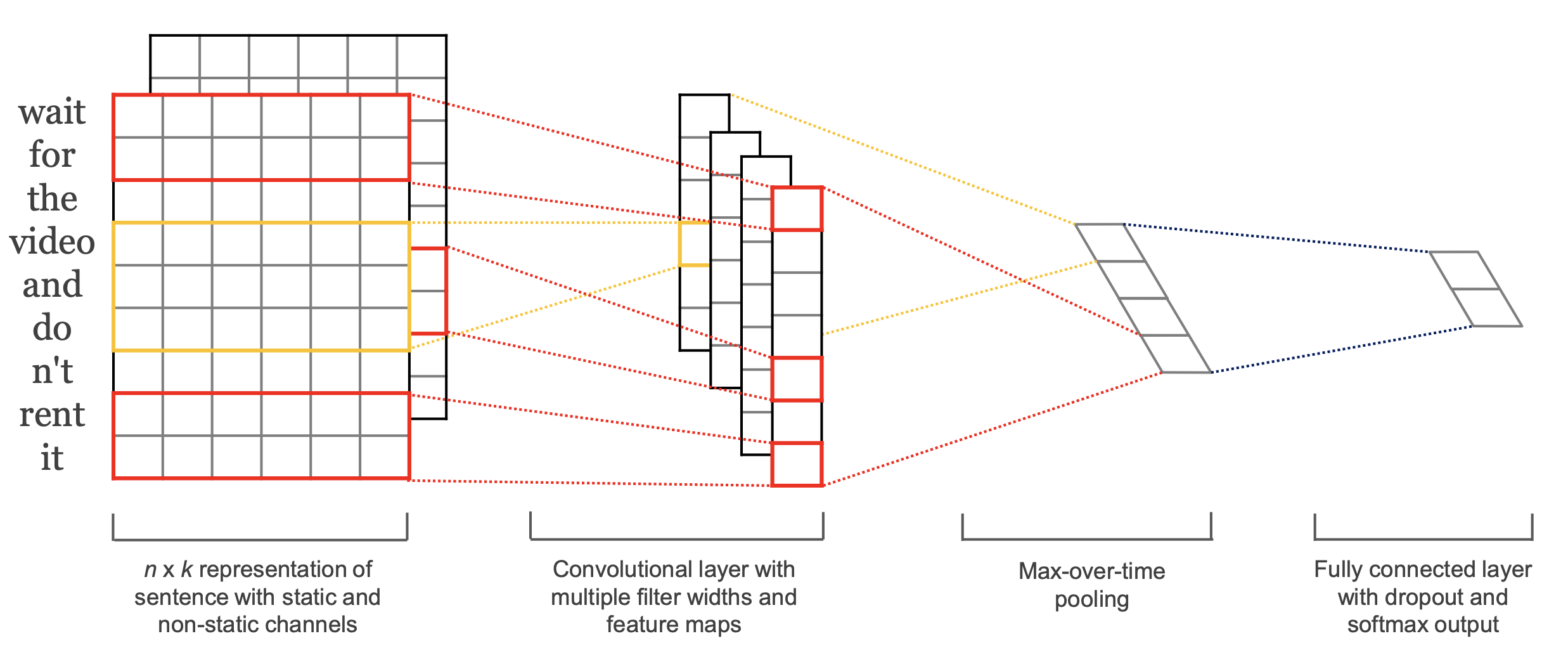
第2步：使用PyTorch编程实现模型

import time
import torch
from torch import nn, optim
from torch.utils.data import random_split, DataLoader
from torchtext.data import get_tokenizer, to_map_style_dataset
from torchtext.datasets import AG_NEWS
from torchtext.vocab import build_vocab_from_iterator

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# 加载AG_NEWS数据集
train_iter, test_iter = AG_NEWS(root='./data')

# 定义tokenizer
tokenizer = get_tokenizer('basic_english')


# 定义数据处理函数
def yield_tokens(data_iter):
    for _, text in data_iter:
        yield tokenizer(text)


# 构建词汇表
vocab = build_vocab_from_iterator(yield_tokens(train_iter), specials=["<unk>"])
vocab.set_default_index(vocab["<unk>"])

# 将数据集映射到MapStyleDataset格式
train_dataset = list(to_map_style_dataset(train_iter))
test_dataset = list(to_map_style_dataset(test_iter))
# 划分验证集
num_train = int(len(train_dataset) * 0.9)
train_dataset, val_dataset = random_split(train_dataset, [num_train, len(train_dataset) - num_train])

text_pipeline = lambda x: vocab(tokenizer(x))
label_pipeline = lambda x: int(x) - 1
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")


def collate_batch(batch):
    label_list, text_list, offsets = [], [], [0]
    for (_label, _text) in batch:
        label_list.append(label_pipeline(_label))
        processed_text = torch.tensor(text_pipeline(_text), dtype=torch.int64)
        text_list.append(processed_text)
        offsets.append(processed_text.size(0))
    label_list = torch.tensor(label_list, dtype=torch.int64)
    offsets = torch.tensor(offsets[:-1]).cumsum(dim=0)
    text_list = torch.cat(text_list)
    return label_list.to(device), text_list.to(device), offsets.to(device)


BATCH_SIZE = 64
# 构建数据集的数据加载器
train_dataloader = DataLoader(train_dataset, batch_size=BATCH_SIZE,
                              shuffle=True, collate_fn=collate_batch)
valid_dataloader = DataLoader(val_dataset, batch_size=BATCH_SIZE,
                              shuffle=True, collate_fn=collate_batch)
test_dataloader = DataLoader(test_dataset, batch_size=BATCH_SIZE,
                             shuffle=True, collate_fn=collate_batch)

class CNN_Text(nn.Module):
    def __init__(self, vocab_size, embed_dim, class_num=4, dropout=0.5, kernel_size: list = None):
        super(CNN_Text, self).__init__()
        if kernel_size is None:
            kernel_size = [3, 4, 5]
        self.embedding = nn.EmbeddingBag(vocab_size, embed_dim, sparse=False)
        self.convs = nn.ModuleList(
            [nn.Conv1d(in_channels=1, out_channels=256, kernel_size=k) for k in kernel_size])
        self.fc = nn.Sequential(
            nn.Dropout(p=dropout),
            nn.Linear(256 * len(kernel_size), 256),
            nn.ReLU(),
            nn.Dropout(p=dropout),
            nn.Linear(256, class_num)
        )

    def forward(self, text, offsets):
        embedded = self.embedding(text, offsets)
        embedded = embedded.unsqueeze(0)
        embedded = embedded.permute(1, 0, 2)
        conv_outputs = []
        for conv in self.convs:
            conv_outputs.append(nn.functional.relu(conv(embedded)))
        pooled_outputs = []
        for conv_output in conv_outputs:
            pooled = nn.functional.max_pool1d(conv_output, conv_output.shape[-1]).squeeze(-1)
            pooled_outputs.append(pooled)
        cat = torch.cat(pooled_outputs, dim=-1)
        return self.fc(cat)

# 设置超参数
vocab_size = len(vocab)
embed_dim = 64
class_num = len(set([label for label, _ in train_iter]))
lr = 1e-3
dropout = 0.5
epochs = 10

# 创建模型、优化器和损失函数
model = CNN_Text(vocab_size, embed_dim, class_num, dropout).to(device)
optimizer = optim.Adam(model.parameters(), lr=lr)
criterion = nn.CrossEntropyLoss()

def train(dataloader):
    model.train()

    for label, text, offsets in dataloader:
        optimizer.zero_grad()
        predicted_label = model(text, offsets)
        loss = criterion(predicted_label, label)
        loss.backward()
        torch.nn.utils.clip_grad_norm_(model.parameters(), 0.1)
        optimizer.step()

def evaluate(dataloader):
    model.eval()
    total_acc, total_count = 0, 0

    with torch.no_grad():
        for label, text, offsets in dataloader:
            predicted_label = model(text, offsets)
            criterion(predicted_label, label)
            total_acc += (predicted_label.argmax(1) == label).sum().item()
            total_count += label.size(0)
    return total_acc / total_count

max_accu = 0
for epoch in range(1, epochs + 1):
    epoch_start_time = time.time()
    train(train_dataloader)
    accu_val = evaluate(valid_dataloader)
    print('-' * 59)
    print('| end of epoch {:3d} | time: {:5.2f}s | '
          'valid accuracy {:8.1f}% '.format(epoch,
                                            time.time() - epoch_start_time,
                                            accu_val * 100))
    print('-' * 59)
    if max_accu < accu_val:
        best_model = model
        max_accu = accu_val

-----------------------------------------------------------
| end of epoch   1 | time: 13.36s | valid accuracy     57.3% 
-----------------------------------------------------------
-----------------------------------------------------------
| end of epoch   2 | time: 10.13s | valid accuracy     77.8% 
-----------------------------------------------------------
-----------------------------------------------------------
| end of epoch   3 | time: 10.27s | valid accuracy     83.3% 
-----------------------------------------------------------
-----------------------------------------------------------
| end of epoch   4 | time: 10.70s | valid accuracy     85.4% 
-----------------------------------------------------------
-----------------------------------------------------------
| end of epoch   5 | time: 10.66s | valid accuracy     86.1% 
-----------------------------------------------------------
-----------------------------------------------------------
| end of epoch   6 | time: 10.63s | valid accuracy     86.5% 
-----------------------------------------------------------
-----------------------------------------------------------
| end of epoch   7 | time: 10.72s | valid accuracy     86.6% 
-----------------------------------------------------------
-----------------------------------------------------------
| end of epoch   8 | time: 10.75s | valid accuracy     86.6% 
-----------------------------------------------------------
-----------------------------------------------------------
| end of epoch   9 | time: 10.65s | valid accuracy     86.8% 
-----------------------------------------------------------
-----------------------------------------------------------
| end of epoch  10 | time: 11.39s | valid accuracy     86.5% 
-----------------------------------------------------------

# 在测试集上测试模型
test_acc = 0.0
with torch.no_grad():
    for label, text, offsets in test_dataloader:
        output = best_model(text, offsets)
        pred = output.argmax(dim=1)
        test_acc += (pred == label).sum().item()
test_acc /= len(test_dataset)

print(f"Test Acc: {test_acc * 100 :.1f}%")

Test Acc: 86.9%

ag_news_label = {1: "World",
                 2: "Sports",
                 3: "Business",
                 4: "Sci/Tec"}

def predict(text, text_pipeline):
    with torch.no_grad():
        text = torch.tensor(text_pipeline(text))
        output = best_model(text, torch.tensor([0]))
        return output.argmax(1).item() + 1

ex_text_str = """
Our younger Fox Cubs (Y2-Y4) also had a great second experience of swimming competition in February when they travelled 
over to NIS at the end of February to compete in the SSL Development Series R2 event. For students aged 9 and under 
these SSL Development Series events are a great introduction to competitive swimming, focussed on fun and participation 
whilst also building basic skills and confidence as students build up to joining the full SSL team in Year 5 and beyond.
"""
best_model = best_model.to("cpu")
print("This is a %s news" % ag_news_label[predict(ex_text_str, text_pipeline)])

This is a World news

习题24.8

  设有输入矩阵$X$和核矩阵$W$：

$$X=[x_{ij}]=\left[\begin{array}{ccccc}{x}_{11}& x_{12}& x_{13}& x_{14}& x_{15}\\ x_{21}& x_{22}& x_{23}& x_{24}& x_{25}\\ x_{31}& x_{32}& x_{33}& x_{34}& x_{35}\\ x_{41}& x_{42}& x_{43}& x_{44}& x_{45}\end{array}\right],W=[w_{mn}]=\left[\begin{array}{ccc}{w}_{11}& w_{12}& w_{13}\\ w_{21}& w_{22}& w_{23}\\ w_{31}& w_{32}& w_{33}\end{array}\right]$$

有卷积$Y=W\ast X$：

$$Y=[y_{kl}]=\left[\begin{array}{ccc}{y}_{11}& y_{12}& y_{13}\\ y_{21}& y_{22}& y_{23}\\ y_{31}& y_{32}& y_{33}\end{array}\right]$$

求${\displaystyle \frac{\partial Y}{\partial W}}$和${\displaystyle \frac{\partial Y}{\partial X}}$，并具体地写出${\displaystyle \frac{\text{d}{y}_{kl}}{\text{d}{w}_{mn}}}$和${\displaystyle \frac{\text{d}{y}_{kl}}{\text{d}{x}_{ij}}}$。

解答：

解答思路：

1. 给出二维卷积定义
2. 计算 ${\displaystyle \frac{\partial Y}{\partial W}}$和${\displaystyle \frac{\partial Y}{\partial X}}$
3. 计算 ${\displaystyle \frac{\text{d}{y}_{kl}}{\text{d}{w}_{mn}}}$和${\displaystyle \frac{\text{d}{y}_{kl}}{\text{d}{x}_{ij}}}$

解答步骤：

第1步：二维卷积定义

  根据书中第24章的本章概要的二维卷积的定义：

  给定输入矩阵$X=[x_{ij}{]}_{I\times J}$，核矩阵$W=[w_{mn}{]}_{M\times N}$。让核矩阵在输入矩阵上按顺序滑动，（二维）卷积是定义在核矩阵与输入矩阵的子矩阵的内积，产生输出矩阵$Y=[y_{kl}{]}_{K\times L}$。

$$Y=W\ast X$$

其中，$Y=[y_{kl}{]}_{K\times L}$。

$$y_{kl}=\sum _{m=1}^M\sum _{n=1}^N{w}_{m,n}{x}_{k+m-1,l+n-1}$$

其中，$k=1,2,\cdots ,K,l=1,2,\cdots ,L,K=I-M+1,L=J-N+1$。

第2步：计算 ${\displaystyle \frac{\partial Y}{\partial W}}$和${\displaystyle \frac{\partial Y}{\partial X}}$

1. 计算 ${\displaystyle \frac{\partial Y}{\partial W}}$

$$\begin{array}{rl}\frac{\partial Y}{\partial W}& =\frac{\partial Y}{\partial w_{m,n}}\\ & =\sum _{k=1}^K\sum _{l=1}^L\frac{\partial y_{kl}}{\partial w_{m,n}}\cdot \frac{\partial Y}{\partial y_{kl}}\\ & =\sum _{k=1}^K\sum _{l=1}^L\frac{\partial (w_{m,n}{x}_{k+m-1,l+n-1})}{\partial w_{m,n}}\cdot \frac{\partial Y}{\partial y_{kl}}\\ & =\sum _{k=1}^K\sum _{l=1}^L{x}_{k+m-1,l+n-1}\cdot \frac{\partial Y}{\partial y_{kl}}\end{array}$$

2. 计算 ${\displaystyle \frac{\partial Y}{\partial X}}$

根据二维卷积的定义，可得：

$$\begin{gathered} m=i-k+1 \\ n=j-l+1 \end{gathered}$$

则：

$$\begin{array}{rl}\frac{\partial Y}{\partial X}& =\frac{\partial Y}{\partial x_{ij}}\\ & =\sum _{k=1}^K\sum _{l=1}^L\frac{\partial y_{kl}}{\partial x_{ij}}\cdot \frac{\partial Y}{\partial y_{kl}}\\ & =\sum _{k=1}^K\sum _{l=1}^L\frac{\partial (w_{i-k+1,j-l+1}{x}_{ij})}{\partial x_{ij}}\cdot \frac{\partial Y}{\partial y_{kl}}\\ & =\sum _{k=1}^K\sum _{l=1}^L{w}_{i-k+1,j-l+1}\cdot \frac{\partial Y}{\partial y_{kl}}\end{array}$$

第3步：计算 ${\displaystyle \frac{\text{d}{y}_{kl}}{\text{d}{w}_{mn}}}$和${\displaystyle \frac{\text{d}{y}_{kl}}{\text{d}{x}_{ij}}}$

1. 计算 ${\displaystyle \frac{\text{d}{y}_{kl}}{\text{d}{w}_{mn}}}$

$$\begin{array}{rl}\frac{\text{d}{y}_{kl}}{\text{d}{w}_{mn}}& =\frac{{\displaystyle \text{d}\left(\sum _{m=1}^M\sum _{n=1}^N{w}_{m,n}{x}_{k+m-1,l+n-1}\right)}}{d{w}_{mn}}\\ & =x_{k+m-1,l+n-1}\end{array}$$

2. 计算 ${\displaystyle \frac{\text{d}{y}_{kl}}{\text{d}{x}_{ij}}}$

  首先计算 ${\displaystyle \frac{\text{d}{y}_{kl}}{\text{d}{x}_{k+m-1,l+n-1}}}$

$$\begin{array}{rl}\frac{\text{d}{y}_{kl}}{\text{d}{x}_{k+m-1,l+n-1}}& =\frac{{\displaystyle \text{d}\left(\sum _{m=1}^M\sum _{n=1}^N{w}_{m,n}{x}_{k+m-1,l+n-1}\right)}}{\text{d}{x}_{k+m-1,l+n-1}}\\ & =w_{mn}\end{array}$$

  令$i=k+m-1$，且当$m=1$时，$i=k$，当$m=M$时，$i=k+M-1$；令$j=l+n-1$，且当$n=1$时，$j=l$，当$n=N$时，$j=l+N-1$。

  则当 $i\in [k,k+M-1]$ 且 $j\in [l,l+N-1]$时，可得：

$$\frac{\text{d}{y}_{kl}}{\text{d}{x}_{ij}}=w_{mn}=w_{i-k+1,i-l+1}$$

  当 $i\notin [k,k+M-1]$ 或 $j\notin [l,l+N-1]$时，可得：

$$\frac{\text{d}{y}_{kl}}{\text{d}{x}_{ij}}=0$$

  综上，

$$\frac{\text{d}{y}_{kl}}{\text{d}{x}_{ij}}=\{\begin{array}{ll}{w}_{i-k+1,i-l+1},& \text{if }i\in [k,k+M-1]\mathrm{且}j\in [l,l+N-1]\\ 0,& \text{otherwise}\end{array}$$

习题24.9

  设有输入矩阵$X$和核矩阵$W$：

$$X=\left[\begin{array}{ccc}{x}_{11}& x_{12}& x_{13}\\ x_{21}& x_{22}& x_{23}\\ x_{31}& x_{32}& x_{33}\end{array}\right],W=\left[\begin{array}{ccc}{w}_{11}& w_{12}& w_{13}\\ w_{21}& w_{22}& w_{23}\\ w_{31}& w_{32}& w_{33}\end{array}\right]$$

验证$\text{rot180}(W)\ast X=\text{rot180}(X)\ast W$成立。

解答：

解答思路：

1. 给出机器学习卷积的定义
2. 计算$\text{rot180}(W)\ast X$
3. 计算$\text{rot180}(X)\ast W$
4. 验证$\text{rot180}(W)\ast X$与$\text{rot180}(X)\ast W$是否相等

解答步骤：

第1步：给出机器学习卷积的定义

  根据书中第24章的本章概要的二维卷积的定义：

  给定输入矩阵$X=[x_{ij}{]}_{I\times J}$，核矩阵$W=[w_{mn}{]}_{M\times N}$。让核矩阵在输入矩阵上按顺序滑动，（二维）卷积是定义在核矩阵与输入矩阵的子矩阵的内积，产生输出矩阵$Y=[y_{kl}{]}_{K\times L}$。

$$Y=W\ast X$$

其中，$Y=[y_{kl}{]}_{K\times L}$。

$$y_{kl}=\sum _{m=1}^M\sum _{n=1}^N{w}_{m,n}{x}_{k+m-1,l+n-1}$$

其中，$k=1,2,\cdots ,K,l=1,2,\cdots ,L,K=I-M+1,L=J-N+1$。

第2步：计算$\text{rot180}(W)\ast X$

  由题意已知：

$$\text{rot180}(W)=[w_{m,n}^{\prime }]=[w_{4-m,4-n}]$$

  由机器学习卷积定义，可得：

$$\begin{array}{rl}{Y}^{\prime }& =\text{rot180}(W)\ast X\\ & =[y_{kl}^{\prime }]\\ & =\sum _{m=1}^3\sum _{n=1}^3{w}_{m,n}^{\prime }{x}_{k+m-1,l+n-1}\\ & =\sum _{m=1}^3\sum _{n=1}^3{w}_{4-m,4-n}{x}_{k+m-1,l+n-1}\end{array}$$

第3步：计算$\text{rot180}(X)\ast W$

  由题意已知：

$$\text{rot180}(X)=[x_{i,j}^{\prime }]=[x_{4-i,4-j}]$$

  由机器学习卷积定义，可得：

$$\begin{array}{rl}{Y}^{″}& =\text{rot180}(X)\ast W\\ & =[y_{kl}^{″}]\\ & =\sum _{i=1}^3\sum _{j=1}^3{x}_{i,j}^{\prime }{w}_{k+i-1,l+j-1}\\ & =\sum _{i=1}^3\sum _{j=1}^3{x}_{4-i,4-j}{w}_{k+i-1,l+j-1}\end{array}$$

第4步：验证$\text{rot180}(W)\ast X$与$\text{rot180}(X)\ast W$是否相等

  由上述计算可知：

$$\begin{gathered} Y^{\prime }=\sum _{m=1}^3\sum _{n=1}^3{w}_{4-m,4-n}{x}_{k+m-1,l+n-1} \\ {Y}^{″}=\sum _{i=1}^3\sum _{j=1}^3{x}_{4-i,4-j}{w}_{k+i-1,l+j-1} \end{gathered}$$

  令 $4-q=k+i-1$，且当$i=1$时，$q=4-k$，当$i=3$时，$q=2-k$；

  又令 $4-p=l+j-1$，且当$j=1$时，$p=4-l$，当$j=3$时，$p=2-l$，

  则

$$\begin{gathered} i=5-q-k \\ j=5-p-l \end{gathered}$$

  因此

$$\begin{array}{rl}{Y}^{″}& =[y_{k,l}^{″}]\\ & =\sum _{i=1}^3\sum _{j=1}^3{x}_{4-i,4-j}{w}_{k+i-1,l+j-1}\\ & =\sum _{q=4-k}^{2-k}\sum _{p=4-l}^{2-l}{w}_{4-q,4-p}{x}_{k+q-1,l+p-1}\end{array}$$

  综上，$Y^{\prime }=Y^{″}$，即 $\text{rot180}(W) * X = \text{rot180}(X) * W $，原命题得证。

习题24.10

  解释残差网络为什么能防止梯度消失和梯度爆炸。

解答：

解答思路：

1. 给出残差网络的基本概念
2. 描述梯度消失和梯度爆炸的现象
3. 解释残差网络能防止梯度消失和梯度爆炸的原因

解答步骤：

第1步：残差网络的基本概念

  根据书中第24章的本章概要的残差网络的描述：

  残差网络是为了解决深度神经网络训练困难而提出的深度学习方法。假设要学习的真实模型是函数 $h(x)$，也可以写作

$$h(x)=x+(h(x)-x)$$

  残差网络的想法是用一个神经网络 $f(x)$ 近似残差 $h(x)-x$，用 $x+f(x)$ 近似真实模型 $h(x)$，整个过程以递归的方式进行。

$$x_i=x_i-1+f_i(x_i-1),i=1,2,\cdots ,n$$

  残差网络由很多个残差单元串联连接组成。每一个残差单元相当于一般的前馈网络的两层，每一层由线性变换和非线性变换组成，还有一个残差连接。
  残差单元的输入是向量 $x$，输出是向量 $y$ 时，整个单元的运算是

$$\begin{gathered} f(x)=W_2\text{relu}(W_{1}x) \\ y=\text{relu}(x+f(x)) \end{gathered}$$

  残差网络可以展开成多个神经网络模块的集成，有很强的表示和学习能力。

第2步：梯度消失和梯度爆炸的现象

  根据书中第23.2.5节的梯度消失与梯度爆炸：

  深度神经网络学习中有时会出现梯度消失(vanishing gradient)或者梯度爆炸(exploding gradient)现象。使用反向传播算法时，首先通过正向传播计算神经网络各层的输出，然后通过反向传播神经网络各层的误差以及梯度，接着利用梯度下降公式对神经网络各层的参数进行更新。在这个过程中，各层的梯度，特别是前面层的梯度，有时会接近0（梯度消失）或接近无穷（梯度爆炸）。梯度消失会导致参数更新停止，梯度爆炸会导致参数溢出，都会使学习无法有效地进行。 反向传播中，首先计算误差向量：

$$\begin{array}{}\text{(23.57)}& {\delta }^{(t-1)}=\{\text{diag}\left(\frac{\partial a}{\partial z^{(t-1)}}\right)\cdot {W^{(t)}}^T\}\cdot {\delta }^{(t)}\end{array}$$

之后计算梯度：

$$\begin{array}{}\text{(23.58)}& \{\begin{array}{l}{\mathrm{\nabla }}_{W^{(t)}}L={\delta }^{(t)}\cdot {h^{(t-1)}}^T\\ {\mathrm{\nabla }}_{b^{(t)}}L={\delta }^{(t)}\end{array}\end{array}$$

造成梯度消失和梯度爆炸的原因有两种：

1. 每一层的误差向量实际由矩阵的连乘决定，连乘得到的矩阵的元素可能会接近0，也可能会接近无穷，导致梯度的元素也会接近0或接近无穷，而且越是前面的层，这个问题就越严重。
2. 得到每一层的误差向量之前，每个元素乘以激活函数的导数，如果激活函数的导数过小，也容易引起梯度消失，而且越是前面的层，这个问题就越严重。

  假设 $L$ 表示神经网络的层数，$w_{i,j}^{(l)}$ 表示第 $l$ 层中第 $i$ 个神经元到第 $l+1$ 层中第 $j$ 个神经元的权重，$a_i^{(l)}$ 表示第 $l$ 层中第 $i$ 个神经元的激活值，$z_i^{(l)}$ 表示第 $l$ 层中第 $i$ 个神经元的加权输入，$g(z)$ 表示激活函数，$y$ 表示网络的输出值，$y_i$ 表示输出向量的第 $i$ 个元素。则网络的输出可以表示为：

$$y=g\left(z^{(L)}\right)=g\left({\mathit{w}}^{(L)}g\left({\mathit{w}}^{(L-1)}g(\cdots g\left({\mathit{w}}^{(1)}\mathit{x}\right))\right)\right)$$

其中 $\mathit{x}$表示输入变量。

  对于一个损失函数 $J(y,\hat{y})$，网络的参数 $\mathit{w}$ 可以通过梯度下降法来更新：

$${\mathit{w}}_{t+1}={\mathit{w}}_t-\eta \frac{\partial J(y,\hat{y})}{\partial \mathit{w}}$$

  在反向传播过程中，可以通过链式法则来计算每个神经元的梯度。具体地，对于第 $l$ 层中第 $i$ 个神经元的梯度，可以表示为：

$$\frac{\partial J}{\partial z_i^{(l)}}=\sum _{j=1}^{m^{(l+1)}}\frac{\partial J}{\partial z_j^{(l+1)}}\frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}}$$

其中 $m^{(l+1)}$ 表示第 $l+1$ 层的神经元数量。然后，可以使用梯度下降法来更新参数。

  因为梯度是从输出层向输入层反向传播的，则梯度的大小可以表示为：

$$\left|\frac{\partial J}{\partial z_i^{(l)}}\right|=\left|\sum _{j=1}^{m^{(l+1)}}\frac{\partial J}{\partial z_j^{(l+1)}}\frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}}\right|.$$

  由于 $z_j^{(l+1)}$ 依赖于 $z_i^{(l)}$，因此 $\frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}}$ 可能会接近0或接近无穷，导致梯度爆炸或梯度消失的情况。

  如果 $\displaystyle \left| \frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}} \right| > 1 $，那么在反向传播时，梯度会呈现指数级增长，导致梯度爆炸的问题。这种情况通常会导致权重的值变得非常大，从而使模型无法收敛。

  相反，如果 ${\displaystyle \left|\frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}}\right|<1}$，那么在反向传播时梯度会逐渐变小，导致梯度消失的问题。这种情况通常会导致网络无法学习到深层特征，从而导致模型性能下降。

第3步：解释残差网络能防止梯度消失和梯度爆炸的原因

  在残差网络中，每个残差单元可以表示为 $y=f(x)+x$，其中 $x$ 表示输入，$f(x)$ 表示卷积层的输出，$y$ 表示残差单元的输出。从数学的角度来看，这个残差单元可以被看作是一个恒等映射加上一个残差映射，即 $y=x+\mathrm{\Delta }(x)$，其中 $\mathrm{\Delta }(x)=f(x)-x$ 表示残差。

  简单地，考虑这个残差单元的导数。计算 $y$ 对 $x$ 的导数有：

$$\frac{\partial y}{\partial x}=\frac{\partial y}{\partial f(x)}\frac{\partial f(x)}{\partial x}+\frac{\partial y}{\partial x}=\frac{\partial f(x)}{\partial x}+1$$

  残差网络能防止梯度消失和梯度爆炸的原因如下：

1. 由于残差网络中的 ${\displaystyle \frac{\partial f(x)}{\partial x}}$不可能一直为-1，因此在残差网络中不容易出现梯度消失的问题。

2. 由于残差网络中的残差映射是通过将输入直接加到输出上实现的，因此它不会影响导数的大小。这意味着如果 ${\displaystyle \frac{\partial y}{\partial x}}$ 接近于 1，那么 ${\displaystyle \frac{\partial J}{\partial x}}$（$J$ 表示损失函数）的值也会比较稳定，不会出现梯度消失或梯度爆炸的问题。

3. 由于残差映射中的 $\mathrm{\Delta }(x)$ 只包含了局部信息，而没有涉及到全局信息，因此它通常不会影响梯度的大小。这意味着即使 ${\displaystyle \frac{\partial y}{\partial x}}$ 很小，梯度也可以通过残差映射传递到后面的层中，从而避免了梯度消失的问题。

参考文献

【1】Yoon Kim. 2014. Convolutional Neural Networks for Sentence Classification[J]. cs.CL, abs/1408.5882