第18章概率潜在语义分析

习题18.1

证明生成模型与共现模型是等价的。

解答：

解答思路：

生成模型的定义
共现模型的定义
证明生成模型与共现模型是等价的

解答步骤：

第1步：生成模型

根据书中第18.1.2节的生成模型的定义：

假设有单词集合 $W = {w_{1}, w_{2}, \dots, w_{M}}$ ，其中 $M$ 是单词个数；文本（指标）集合 $D = {d_{1}, d_{2}, \dots, d_{N}}$ ，其中 $N$ 是文本个数；话题集合 $Z = {z_{1}, z_{2}, \dots, z_{K}}$ ，其中 $K$ 是预先设定的话题个数。随机变量 $w$ 取值于单词集合；随机变量 $d$ 取值于文本集合，随机变量 $z$ 取值于话题集合。概率分布 $P (d)$ 、条件概率分布 $P (z | d)$ 、条件概率分布 $P (w | z)$ 皆属于多项分布，其中 $P (d)$ 表示生成文本 $d$ 的概率， $P (z | d)$ 表示文本 $d$ 生成话题 $z$ 的概率， $P (w | z)$ 表示话题 $z$ 生成单词 $w$ 的概率。
每个单词-文本对 $(w, d)$ 的生成概率由以下公式决定：
$\begin{matrix} (1) & \begin{aligned} P (w, d) & = P (d) P (w | d) \\ = P (d) \sum_{z} P (w, z | d) \\ = P (d) \sum_{z} P (z | d) P (w | z) \end{aligned} \end{matrix}$
即生成模型的定义。
生成模型假设在话题 $z$ 给定条件下，单词 $w$ 与文本 $d$ 条件独立，即
$P (w, z | d) = P (z | d) P (w | z)$

第2步：共现模型

根据书中第18.1.3节的共现模型的定义：

每个单词-文本对 $(w, d)$ 的概率由以下公式决定：
$\begin{matrix} (2) & P (w, d) = \sum_{z \in Z} P (z) P (w | z) P (d | z) \end{matrix}$
即共现模型的定义。
共现模型假设在话题 $z$ 给定条件下，单词 $w$ 与文本 $d$ 是条件独立的，即
$P (w, d | z) = P (w | z) P (d | z)$

第3步：证明生成模型与共现模型是等价的

结合公式(1)和公式(2)，可得：

\begin{aligned} P (w, d) & = P (d) \sum_{z} P (z | d) P (w | z) \\ = \sum_{z} P (w | z) P (z | d) P (d) \\ = \sum_{z} P (w, z | d) P (d) \\ = \sum_{z} P (w, d, z) \\ = \sum_{z} P (z) P (w, d | z) \\ = \sum_{z} P (z) P (w | z) P (d | z) \end{aligned}

可知生成模型与共现模型的概率公式是等价的，故证得生成模型与共现模型是等价的。

习题18.2

推导共现模型的EM算法。

解答：

解答思路：

EM算法的一般步骤
推导共现模型的 $Q$ 函数
推导共现模型的E步
推导共现模型的M步
写出共现模型的EM算法

解答步骤：

第1步：EM算法

根据书中第18.2节的EM算法介绍：

EM算法是一种迭代算法，每次迭代包括交替的两步：E步，求期望；M步，求极大。E步是计算 $Q$ 函数，即完全数据的对数似然函数对不完全数据的条件分布的期望。M步是对 $Q$ 函数极大化，更新模型参数。详细介绍见第9章。

第2步：推导共现模型的 $Q$ 函数推导

设单词集合为 $W = {w_{1}, w_{2}, \dots, w_{M}}$ ，文本集合为 $D = {d_{1}, d_{2}, \dots, d_{N}}$ ，话题集合为 $Z = {z_{1}, z_{2}, \dots, z_{K}}$ 。给定单词-文本共现数据 $T = {n (w_{i}, d_{j})}, i = 1, 2, \dots, M, j = 1, 2, \dots, N$ ，目标是估计概率潜在语义模型（共现模型）的参数。

根据书中第18.1.3节的共现模型定义：

文本-单词共现数据 $T$ 的生成概率为所有单词-文本对 $(w, d)$ 的生成概率的乘积：
$\begin{matrix} (1) & P (T) = \prod_{(w, d)} P (w, d)^{n (w, d)} \end{matrix}$
每个单词-文本对 $(w, d)$ 的概率由以下公式决定：
$\begin{matrix} (2) & P (w, d) = \sum_{z \in Z} P (z) P (w | z) P (d | z) \end{matrix}$
即共现模型的定义。

对公式（1）使用极大似然估计，结合公式（2），对数似然函数是

\begin{aligned} \log P (T) & = \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \log P (w_{i}, d_{j}) \\ = \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \log [\sum_{k = 1}^{K} P (z_{k}) P (w_{i} | z_{k}) P (d_{j} | z_{k})] \end{aligned}

由于 $\log$ 函数是上凸函数，可以基于Jessen不等式，得：

\begin{aligned} \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \log [\sum_{k = 1}^{K} P (z_{k}) P (w_{i} | z_{k}) P (d_{j} | z_{k})] \\ ⩾ & \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \sum_{k = 1}^{K} \log [P (z_{k}) P (w_{i} | z_{k}) P (d_{j} | z_{k})] \end{aligned}

可以得到 $Q$ 函数：

\begin{aligned} Q & = E_{Z} [\log P (T) | z] \\ = E_{Z} {\sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \sum_{k = 1}^{K} \log [P (z_{k}) P (w_{i} | z_{k}) P (d_{j} | z_{k})]} \\ = \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) E_{Z} {\sum_{k = 1}^{K} \log [P (z_{k}) P (w_{i} | z_{k}) P (d_{j} | z_{k})]} \\ = \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \sum_{k = 1}^{K} P (z_{k} | w_{i}, d_{j}) \log [P (z_{k}) P (w_{i} | z_{k}) P (d_{j} | z_{k})] \end{aligned}

第3步：推导共现模型的E步

根据贝叶斯公式计算

P (z_{k} | w_{i}, d_{j}) = \frac{P (z_{k}) P (w_{i} | z_{k}) P (d_{j} | z_{k})}{\sum_{k = 1}^{K} P (z_{k}) P (w_{i} | z_{k}) P (d_{j} | z_{k})}

第4步：推导共现模型的M步

通过约束最优化求解 $Q$ 函数的极大值，这时 $P (z_{k})$ 、 $P (w_{i} | z_{k})$ 和 $P (d_{j} | z_{k})$ 是变量。因为变量 $P (z_{k})$ 、 $P (w_{i} | z_{k})$ 和 $P (d_{j} | z_{k})$ 形成概率分布，满足约束条件

\begin{array}{ll} \sum_{k = 1}^{K} P (z_{k}) = 1 \\ \sum_{i = 1}^{M} P (w_{i} | z_{k}) = 1, k = 1, 2, \dots, K \\ \sum_{j = 1}^{N} P (d_{j} | z_{k}) = 1, k = 1, 2, \dots, K \end{array}

使用拉格朗日法，引入拉格朗日乘子 $α, β, γ$ ，定义拉格朗日函数 $Λ$

Λ = Q + α (1 - \sum_{k = 1}^{K} P (z_{k})) + \sum_{k = 1}^{K} β_{k} (1 - \sum_{i = 1}^{M} P (w_{i} | z_{k})) + \sum_{k = 1}^{K} γ_{k} (1 - \sum_{j = 1}^{N} P (d_{j} | z_{k}))

将拉格朗日函数 $Λ$ 分别对 $P (z_{k})$ 、 $P (w_{i} | z_{k})$ 和 $P (d_{j} | z_{k})$ 求偏导数，并令其等于0，得到下面的方程组

\begin{array}{lll} \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) P (z_{k} | w_{i}, d_{j}) - α P (z_{k}) = 0, & k = 1, 2, \dots, K \\ \sum_{j = 1}^{N} n (w_{i}, d_{j}) P (z_{k} | w_{i}, d_{j}) - β_{k} P (w_{i} | z_{k}) = 0, & i = 1, 2, \dots, M; & k = 1, 2, \dots, K \\ \sum_{i = 1}^{M} n (w_{i}, d_{j}) P (z_{k} | w_{i}, d_{j}) - γ_{k} P (d_{j} | z_{k}) = 0, & j = 1, 2, \dots, N; & k = 1, 2, \dots, K \end{array}

解方程组得M步的参数估计公式：

\begin{array}{ll} p (z_{k}) = \frac{\sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) P (z_{k} | w_{i}, d_{j})}{\sum_{j = 1}^{N} n (d_{j})} \\ p (w_{i} | z_{k}) = \frac{\sum_{j = 1}^{N} n (w_{i}, d_{j}) P (z_{k} | w_{i}, d_{j})}{\sum_{m = 1}^{M} \sum_{j = 1}^{N} n (w_{m}, d_{j}) P (z_{k} | w_{m}, d_{j})} \\ p (d_{j} | z_{k}) = \frac{\sum_{i = 1}^{M} n (w_{i}, d_{j}) P (z_{k} | w_{i}, d_{j})}{\sum_{i = 1}^{M} \sum_{l = 1}^{N} n (w_{i}, d_{l}) P (z_{k} | w_{i}, d_{l})} \end{array}

第5步：共现模型的EM算法

输入：设单词集合为 $W = {w_{1}, w_{2}, \dots, w_{M}}$ ，文本集合为 $D = {d_{1}, d_{2}, \dots, d_{N}}$ ，话题集合为 $Z = {z_{1}, z_{2}, \dots, z_{K}}$ ，共现数据 ${n (w_{i}, d_{j})}, i = 1, 2, \dots, M, j = 1, 2, \dots, N$ ；
输出： $P (z_{k})$ 、 $P (w_{i} | z_{k})$ 和 $P (d_{j} | z_{k})$ 。
（1）设置参数 $P (z_{k})$ 、 $P (w_{i} | z_{k})$ 和 $P (d_{j} | z_{k})$ 的初始值。
（2）迭代执行以下E步、M步，直到收敛为止。
E步：

P (z_{k} | w_{i}, d_{j}) = \frac{P (z_{k}) P (w_{i} | z_{k}) P (d_{j} | z_{k})}{\sum_{k = 1}^{K} P (z_{k}) P (w_{i} | z_{k}) P (d_{j} | z_{k})}

M步：

\begin{array}{ll} p (z_{k}) = \frac{\sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) P (z_{k} | w_{i}, d_{j})}{\sum_{j = 1}^{N} n (d_{j})} \\ p (w_{i} | z_{k}) = \frac{\sum_{j = 1}^{N} n (w_{i}, d_{j}) P (z_{k} | w_{i}, d_{j})}{\sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) P (z_{k} | w_{i}, d_{j})} \\ p (d_{j} | z_{k}) = \frac{\sum_{i = 1}^{M} n (w_{i}, d_{j}) P (z_{k} | w_{i}, d_{j})}{\sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) P (z_{k} | w_{i}, d_{j})} \end{array}

习题18.3

对以下文本数据集进行概率潜在语义分析。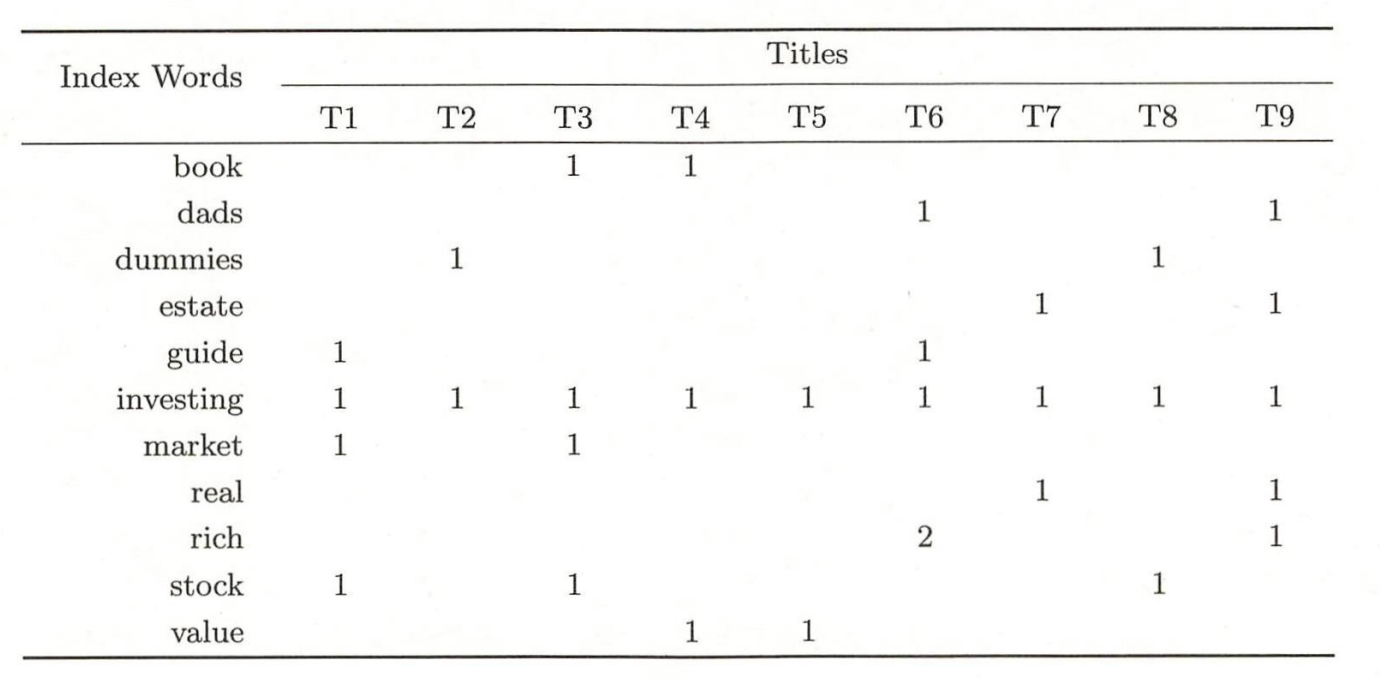

解答：

解答思路：

给出概率潜在语义模型参数估计的EM算法
自编程实现概率潜在语义模型参数估计的EM算法
对文本数据集进行概率潜在语义分析

解答步骤：

第1步：概率潜在语义模型参数估计的EM算法

根据书中第18章的算法18.1的概率潜在语义模型参数估计的EM算法：

算法18.1（概率潜在语义模型参数估计的EM算法）
输入：设单词集合为 $W = {w_{1}, w_{2}, \dots, w_{M}}$ ，文本集合为 $D = {d_{1}, d_{2}, \dots, d_{N}}$ ，话题集合为 $Z = {z_{1}, z_{2}, \dots, z_{K}}$ ，共现数据 ${n (w_{i}, d_{j})}, i = 1, 2, \dots, M, j = 1, 2, \dots, N$ ；
输出： $P (w_{i} | z_{k})$ 和 $P (z_{k} | d_{j})$ 。
（1）设置参数 $P (w_{i} | z_{k})$ 和 $P (z_{k} | d_{j})$ 的初始值。
（2）迭代执行以下E步、M步，直到收敛为止。
E步：
$P (z_{k} | w_{i}, d_{j}) = \frac{P (w_{i} | z_{k}) P (z_{k} | d_{j})}{\sum_{k = 1}^{K} P (w_{i} | z_{k}) P (z_{k} | d_{j})}$
M步：
$\begin{array}{ll} p (w_{i} | z_{k}) = \frac{\sum_{j = 1}^{N} n (w_{i}, d_{j}) P (z_{k} | w_{i}, d_{j})}{\sum_{m = 1}^{M} \sum_{j = 1}^{N} n (w_{m}, d_{j}) P (z_{k} | w_{m}, d_{j})} \\ p (d_{j} | z_{k}) = \frac{\sum_{i = 1}^{M} n (w_{i}, d_{j}) P (z_{k} | w_{i}, d_{j})}{n (d_{j})} \end{array}$

第2步：自编程实现概率潜在语义模型参数估计的EM算法

python

import numpy as np


class EMPlsa:
    def __init__(self, max_iter=100, random_state=2022):
        """
        基于生成模型的EM算法的概率潜在语义模型
        :param max_iter: 最大迭代次数
        :param random_state: 随机种子
        """
        self.max_iter = max_iter
        self.random_state = random_state

    def fit(self, X, K):
        """
        :param X: 单词-文本矩阵
        :param K: 话题个数
        :return: P(w_i|z_k) 和 P(z_k|d_j)
        """
        # M, N分别为单词个数和文本个数
        M, N = X.shape

        # 计算n(d_j)
        n_d = [np.sum(X[:, j]) for j in range(N)]

        # (1)设置参数P(w_i|z_k)和P(z_k|d_j)的初始值
        np.random.seed(self.random_state)
        p_wz = np.random.random((M, K))
        p_zd = np.random.random((K, N))

        # (2)迭代执行E步和M步，直至收敛为止
        for _ in range(self.max_iter):
            # E步
            P = np.zeros((M, N, K))
            for i in range(M):
                for j in range(N):
                    for k in range(K):
                        P[i][j][k] = p_wz[i][k] * p_zd[k][j]
                    P[i][j] /= np.sum(P[i][j])

            # M步
            for k in range(K):
                for i in range(M):
                    p_wz[i][k] = np.sum([X[i][j] * P[i][j][k] for j in range(N)])
                p_wz[:, k] /= np.sum(p_wz[:, k])

            for k in range(K):
                for j in range(N):
                    p_zd[k][j] = np.sum([X[i][j] * P[i][j][k] for i in range(M)]) / n_d[j]

        return p_wz, p_zd

第3步：对文本数据集进行概率潜在语义分析

python

# 输入文本-单词矩阵，共有9个文本，11个单词
X = np.array([[0, 0, 1, 1, 0, 0, 0, 0, 0],
              [0, 0, 0, 0, 0, 1, 0, 0, 1],
              [0, 1, 0, 0, 0, 0, 0, 1, 0],
              [0, 0, 0, 0, 0, 0, 1, 0, 1],
              [1, 0, 0, 0, 0, 1, 0, 0, 0],
              [1, 1, 1, 1, 1, 1, 1, 1, 1],
              [1, 0, 1, 0, 0, 0, 0, 0, 0],
              [0, 0, 0, 0, 0, 0, 1, 0, 1],
              [0, 0, 0, 0, 0, 2, 0, 0, 1],
              [1, 0, 1, 0, 0, 0, 0, 1, 0],
              [0, 0, 0, 1, 1, 0, 0, 0, 0]])

# 设置精度为3
np.set_printoptions(precision=3, suppress=True)

# 假设话题的个数是3个
k = 3

em_plsa = EMPlsa(max_iter=100)

p_wz, p_zd = em_plsa.fit(X, 3)

print("参数P(w_i|z_k)：")
print(p_wz)
print("参数P(z_k|d_j)：")
print(p_zd)

参数P(w_i|z_k)：
[[0.    0.162 0.   ]
 [0.    0.    0.2  ]
 [0.116 0.081 0.   ]
 [0.115 0.    0.1  ]
 [0.    0.081 0.1  ]
 [0.423 0.271 0.2  ]
 [0.    0.162 0.   ]
 [0.115 0.    0.1  ]
 [0.    0.    0.3  ]
 [0.    0.243 0.   ]
 [0.231 0.    0.   ]]
参数P(z_k|d_j)：
[[0.    1.    0.    0.553 1.    0.    1.    0.    0.   ]
 [1.    0.    1.    0.447 0.    0.    0.    1.    0.   ]
 [0.    0.    0.    0.    0.    1.    0.    0.    1.   ]]

第18章 概率潜在语义分析 ​

习题18.1 ​

习题18.2 ​

习题18.3 ​

第18章概率潜在语义分析

习题18.1

习题18.2

习题18.3