第19章 马尔可夫链蒙特卡罗法

习题19.1

  用蒙特卡罗积分法求

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{x}^2\exp (-\frac{x^2}{2})\mathrm{d}x$$

解答：

解答思路：

1. 给出蒙特卡罗积分计算方法。
2. 将被积分的函数分解，得到其数学期望表示形式。
3. 自编程实现，使用样本均值求近似计算积分。

解答步骤

第1步：蒙特卡罗积分计算方法

  根据书中第19.1.3节的关于蒙特卡罗积分法的描述：

  假设有一个函数 $h(x)$，目标是计算该函数的积分

$${\int }_{\mathcal{X}}h(x)\mathrm{d}x$$

  如果能够将函数 $h(x)$ 分解成一个函数 $f(x)$ 和一个概率密度函数 $p(x)$ 的乘积的形式, 那么就有

$${\int }_{\mathcal{X}}h(x)\mathrm{d}x={\int }_{\mathcal{X}}f(x)p(x)\mathrm{d}x=E_{p(x)}[f(x)]$$

于是函数 $h(x)$ 的积分可以表示为函数 $f(x)$ 关于概率密度函数 $p(x)$ 的数学期望。实际上, 给定一个概率密度函数 $p(x)$, 只要取 ${\displaystyle f(x)=\frac{h(x)}{p(x)}}$，就可得上式。就是说, 任何一个函数的积分都可以表示为某一个函数的数学期望的形式。而函数的数学期望又可以通过函数的样本均值估计。于是，就可以利用样本均值来近似计算积分。

$${\int }_{\mathcal{X}}h(x)\mathrm{d}x=E_{p(x)}[f(x)]\approx \frac{1}{n}\sum _{i=1}^{n}f(x_i)$$

第2步：将所积分的函数分解，其得到数学期望表示形式

  取概率密度函数为标准正态分布的密度函数 ${\displaystyle p(x)=\frac{1}{\sqrt{2\pi }}\exp (-\frac{x^2}{2})}$，则

$$f(x)=\frac{h(x)}{p(x)}=\frac{{\displaystyle x^2\exp (-\frac{x^2}{2})}}{{\displaystyle \frac{1}{\sqrt{2\pi }}\exp (-\frac{x^2}{2})}}=\sqrt{2\pi }{x}^2$$

  将原函数积分表示为函数 $f(x)$ 关于概率密度函数 $p(x)$ 的数学期望

$${\int }_{\mathcal{X}}{x}^2\exp (-\frac{x^2}{2})\mathrm{d}x={\int }_{\mathcal{X}}f(x)p(x)\mathrm{d}x=E_{p(x)}[f(x)]$$

第3步：自编程实现，使用样本均值求近似计算积分

import numpy as np


class MonteCarloIntegration:
    def __init__(self, func_f, func_p):
        # 所求期望的函数
        self.func_f = func_f
        # 抽样分布的概率密度函数
        self.func_p = func_p

    def solve(self, num_samples):
        """
        蒙特卡罗积分法
        :param num_samples: 抽样样本数量
        :return: 样本的函数均值
        """
        samples = self.func_p(num_samples)
        vfunc_f = lambda x: self.func_f(x)
        vfunc_f = np.vectorize(vfunc_f)
        y = vfunc_f(samples)
        return np.sum(y) / num_samples

def func_f(x):
    """定义函数f"""
    return x ** 2 * np.sqrt(2 * np.pi)


def func_p(n):
    """定义在分布上随机抽样的函数g"""
    return np.random.standard_normal(int(n))


# 设置样本数量
num_samples = 1e6

# 使用蒙特卡罗积分法进行求解
monte_carlo_integration = MonteCarloIntegration(func_f, func_p)
result = monte_carlo_integration.solve(num_samples)
print("抽样样本数量:", num_samples)
print("近似解:", result)

抽样样本数量: 1000000.0
近似解: 2.5071535842506965

习题19.2

  证明如果马尔可夫链是不可约的，且有一个状态是非周期的，则其他所有状态也是非周期的，即这个马尔可夫链是非周期的。

解答：

解答思路：

1. 给出马尔科夫链的基本定义
2. 给出不可约的定义
3. 给出非周期的定义
4. 证明如果马尔可夫链是不可约的，则所有状态周期都相同
5. 证明原命题

解答步骤：

第1步：马尔可夫链

  根据书中第19章的定义19.1马尔科夫链的基本定义：

定义19.1（马尔科夫链） 考虑一个随机变量的序列$X=\{X_0,X_1,\cdots ,X_t,\cdots \}$，这里$X_t$表示时刻$t$的随机变量，$t=0,1,2,\cdots$。每个随机变量$X_t(t=0,1,2,\cdots )$的取值集合相同，称为状态空间，表示为$\mathcal{S}$。随机变量可以是离散的，也可以是连续的。以上随机变量的序列构成随机过程（stochastic process）。

  假设在时刻0的随机变量$X_0$遵循概率分布$P(X_0)={\pi }_0$，称为初始状态分布。在某个时刻$t⩾1$的随机变量$X_t$与前一时刻的随机变量$X_{t-1}$之间有条件分布$P(X_t|X_{t-1})$，如果$X_t$只依赖于$X_{t-1}$，而不依赖于过去的随机变量$\{X_0,X_1,\cdots ,X_{t-2}\}$，这一性质称为马尔可夫性，即

$$P(X_t|X_0,X_1,\cdots ,X_{t-1})=P(X_t|X_{t-1}),t=1,2,\cdots$$

具有马尔可夫性的随机序列$X=\{X_0,X_1,\cdots ,X_t,\cdots \}$称为马尔可夫链，或马尔可夫过程。条件概率分布$P(X_t|X_{t-1})$称为马尔可夫链的转移概率分布。转移概率分布决定了马尔可夫链的特性。

  根据书中第19.2.2节的状态转移概率：

$$P_{ij}^t=P(X_t=i|X_0=j)$$

表示时刻0从状态$j$出发，时刻$t$到达状态$i$的$t$步转移概率。

第2步：不可约的定义

  根据书中第19章的定义19.3的不可约的定义：

  定义19.3（不可约） 设有马尔可夫链 $X=\{X_0,X_1,\cdots ,X_t,\cdots \}$，状态空间为 $\mathcal{S}$，对于任意状态 $i,j\in \mathcal{S}$，如果存在一个时刻 $t(t>0)$ 满足

$$P(X_t=i|X_0=j)>0$$

也就是说，时刻0从状态 $j$ 出发, 时刻 $t$ 到达状态 $i$ 的概率大于0，则称此马尔可夫链 $X$ 是不可约的（irreducible），否则称马尔可夫链是可约的（reducible）。

第3步：非周期的定义

  根据书中第19章的定义19.4的非周期的定义：

定义19.4（非周期） 设有马尔可夫链 $X=\{X_0,X_1,\cdots ,X_t,\cdots \}$，状态空间为 $\mathcal{S}$，对于任意状态 $i\in \mathcal{S}$，如果时刻0从状态 $i$ 出发，$t$ 时刻返回状态的所有时间长 $\{t:P(X_t=i|X_0=i)>0\}$ 的最大公约数是1，则称此马尔可夫链 $X$ 是非周期的（aperiodic），否则称马尔可夫链是周期的（periodic）。

第4步：证明如果马尔可夫链是不可约的，则所有状态周期都相同

  如果该马尔可夫链是不可约的，则对于 $\mathrm{\forall }i,j\in S$，必然存在时刻 $m,n(m>0,n>0)$ 满足

$$p_{ij}^m>0,p_{ji}^n>0$$

根据状态转移概率的定义，有 $p_{ij}^m=P(X_m=i|X_0=j),p_{ji}^n=P(X_n=j|X_0=i)$

  可得

$$p_{ii}^{m+n}=\sum _{k\in S}{p}_{ik}^m{p}_{ki}^n⩾p_{ij}^m{p}_{ji}^n>0$$

  则必然存在 $s$ 使得 $P_{jj}^s>0$，且满足

$$P_{ii}^{m+n+s}⩾P_{ij}^m{P}_{jj}^s{P}_{ji}^n>0$$

  假设状态 $i,j$ 的周期分别是 $d(i),d(j)$，由上两式可知

$$\begin{gathered} (m+n)modd(i)=0 \\ (m+n+s)modd(i)=0 \end{gathered}$$

  所以 $smodd(i)=0$。

  又因为 $P_{jj}^s>0$，所以 $smodd(j)=0$。因此 $d(i)modd(j)=0$。同理可得 $d(j)modd(i)=0$

  故 $d(i)==d(j)$，可得如果马尔可夫链是不可约的，所有状态周期都是相同的。

第5步：证明原命题

  在不可约的马尔可夫链中如果有一个状态的是非周期的，即其周期为1，则其他所有状态的周期也为1，所以该马尔可夫链是非周期的。原命题得证。

习题19.3

  验证具有以下转移概率矩阵的马尔可夫链是可约的，但是非周期的。

$$P=\left[\begin{array}{cccc}1/2& 1/2& 0& 0\\ 1/2& 0& 1/2& 0\\ 0& 1/2& 0& 0\\ 0& 0& 1/2& 1\end{array}\right]$$

解答：

解答思路：

1. 给出平稳分布的定义
2. 计算该马尔可夫链的平稳分布
3. 验证该马尔可夫链是可约的
4. 验证该马尔可夫链是非周期的

解答步骤：

第1步：平稳分布的定义

  根据书中第19章的定义19.2的平稳分布的定义：

  定义19.2（平稳分布） 设有马尔可夫链 $X=\{X_0,X_1,\cdots ,X_t,\cdots \}$，其状态空间为 $\mathcal{S}$，转移概率矩阵为 $P=(p_{ij})$，如果存在状态空间 $\mathcal{S}$ 上的一个分布

$$\pi =\left[\begin{array}{c}{\pi }_1\\ {\pi }_2\\ ⋮\end{array}\right]$$

使得

$$\pi =P\pi$$

则称 $\pi$ 为马尔可夫链 $X=\{X_0,X_1,\cdots ,X_t,\cdots \}$ 的平稳分布。

  根据书中第19章的引理19.1：

  引理19.1 给定一个马尔可夫链 $ X = {X_0, X_1, \cdots, X_t, \cdots }$，状态空间为 $\mathcal{S}$，转移概率矩阵为 $P=(p_{ij})$，则分布 $\pi =({\pi }_1,{\pi }_2,\cdots {)}^T$ 为 $X$ 的平稳分布的充分必要条件是 $ \pi = (\pi_1, \pi_2, \cdots )^T$ 是下列方程组的解：

$$\begin{array}{l}{\displaystyle x_i=\sum _j{p}_{ij}{x}_j,i=1,2,\cdots }\\ x_i⩾0,i=1,2,\cdots \\ {\displaystyle \sum _i{x}_i=1}\end{array}$$

第2步：计算该马尔可夫链的平稳分布

  设平稳分布为 $\pi =(x_1,x_2,x_3,x_4{)}^T$，则由引理19.1可得

$$\begin{array}{l}{\displaystyle x_1=\frac{1}{2}{x}_1+\frac{1}{2}{x}_2}\\ {\displaystyle x_2=\frac{1}{2}{x}_1+\frac{1}{2}{x}_3}\\ {\displaystyle x_3=\frac{1}{2}{x}_2}\\ {\displaystyle x_4=\frac{1}{2}{x}_3+1x_4}\\ x_1+x_2+x_3+x_4=1\\ x_i⩾0,i=1,2,3,4\end{array}$$

解方程组，得到唯一的平稳分布

$$\pi =(0,0,0,1{)}^T$$

第3步：验证该马尔可夫链是不可约的

  此马尔可夫链，转移到状态4后，就在该状态上循环跳转，不能到达状态1、状态2和状态3，最后停留在状态4，故该马尔可夫链是可约的。

第4步：验证该马尔可夫链是非周期的

1. 对于状态1，它返回状态1的最小时间长为1，故其所有时间长的最大公约数是1；
2. 对于状态2，它通过$2\to 1\to 2$返回状态2的时间长为2，通过$2\to 1\to 1\to 2$返回状态2的时间长为3，故其所有时间长的最大公约数是1
3. 对于状态3，它通过$3\to 2\to 3$返回状态3的时间长为2，通过$3\to 2\to 1\to 1\to 2\to 3$返回状态3的时间长为5，故其所有时间长的最大公约数是1
4. 对于状态4，它返回状态4的最小时间长为1，故其所有时间长的最大公约数是1

综上，该马尔可夫链是非周期的。

习题19.4

  验证具有以下转移概率矩阵的马尔可夫链是不可约的，但是周期性的。

$$P=\left[\begin{array}{cccc}0& 1/2& 0& 0\\ 1& 0& 1/2& 0\\ 0& 1/2& 0& 1\\ 0& 0& 1/2& 0\end{array}\right]$$

解答：

解答思路：

1. 计算该马尔可夫链的平稳分布
2. 验证该马尔可夫链是不可约的
3. 验证该马尔可夫链是周期性的

解答步骤：

第1步：计算该马尔可夫链的平稳分布

  根据书中第19章的定义19.2的平稳分布的定义和引理19.1（同习题19.4），设平稳分布为 $\pi =(x_1,x_2,x_3,x_4{)}^{\mathrm{T}}$，则由引理19.1可得：

$$\begin{array}{l}{\displaystyle x_1=\frac{1}{2}{x}_2}\\ {\displaystyle x_2=1x_1+\frac{1}{2}{x}_3}\\ {\displaystyle x_3=\frac{1}{2}{x}_2+1x_4}\\ {\displaystyle x_4=\frac{1}{2}{x}_3}\\ x_1+x_2+x_3+x_4=1\\ x_i⩾0,i=1,2,3,4\end{array}$$

解方程组，得到唯一的平稳分布

$$\pi =(\frac{1}{6},\frac{1}{3},\frac{1}{3},\frac{1}{6}{)}^T$$

第2步：验证该马尔可夫链是不可约的

  观察到平稳分布各项均大于0，说明此马尔可夫链从任意状态出发，经过若干步之后，可以到达任意状态，故该马尔可夫链是不可约的。

第3步：验证该马尔可夫链是周期性的

  该马尔可夫链的转移仅发生在相邻奇偶状态之间，从每个状态出发，返回该状态的时刻都是2的倍数：$\{2,4,6,\cdots ,2n\},n\in N^{\ast }$。故该马尔可夫链是周期性的，其周期为2。

习题19.5

  证明可逆马尔可夫链一定是不可约的。

解答：

解答思路

1. 给出可逆马尔可夫链的定义
2. 构造特殊的可逆马尔可夫链
3. 验证其是可约的，原命题不成立

解答步骤

第1步：可逆马尔可夫链

  根据书中第19章的定义19.6的可逆马尔可夫链的定义：

  定义19.6（可逆马尔可夫链） 设有马尔可夫链 $ X = {X_0, X_1, \cdots, X_t, \cdots }$，状态空间为 $\mathcal{S}$，转移概率矩阵为 $P$，如果有状态分布 $\pi =({\pi }_1,{\pi }_2,\cdots {)}^T$，对于任意状态 $i,j\in \mathcal{S}$，对任意一个时刻 $t$ 满足

$$P(X_t=i|X_{t-1}=j){\pi }_j=P(X_{t-1}=j|X_t=i){\pi }_i,i,j=1,2,\cdots$$

或简写为

$$p_{ji}{\pi }_j=p_{ij}{\pi }_i,i,j=1,2,\cdots$$

则称此马尔可夫链 $X$ 为可逆马尔可夫链，上式称为细致平衡方程。

第2步：构造特殊的可逆马尔可夫链

  对于以单位矩阵做转移矩阵的马尔可夫链，其转移矩阵P

$$P=\left[\begin{array}{cccc}1& 0& \cdots & 0\\ 0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& 1\end{array}\right]$$

  对于任意平稳分布 $\pi$，满足$P\pi =\pi$ 恒成立，所以该马尔可夫链是可逆的。

第3步：验证其是可约的，原命题被证伪

  对于任意状态 $i\in S$，跳转到其他的状态 $j\in S(j\ne i)$ 的概率始终为0，即 $p_{i,j}^t=0,\mathrm{\forall }t\in N^{\ast }$。所以该马尔可夫链是可约的。

  这与原命题矛盾，故原命题不成立。

习题19.6

  从一般的Metropolis-Hastings算法推导出单分量Metropolis-Hastings算法。

解答：

解答思路：

1. 给出一般的Metropolis-Hastings算法
2. 给出单分量Metropolis-Hastings算法的基本思想
3. 推导单分量Metropolis-Hastings算法

解答步骤：

第1步：一般的Metropolis-Hastings算法

  根据书中第19章的算法19.2的Metropolis-Hastings算法：

算法19.2（Metropolis-Hastings算法）
输入：抽样的目标分布的密度函数$p(x)$，函数$f(x)$；
输出：$p(x)$的随机样本$x_{m+1},x_{m+2},\cdots ,x_n$，函数样本均值$f_{mn}$；
参数：收敛步数$m$，迭代步数$n$。
（1）任意选择一个初始值$x_0$
（2） 对 $i=1,2,\cdots ,n$循环执行
  （a）设状态$x_{i-1}=x$，按照建议分布$q(x,x^{\prime })$随机抽取一个候选状态$x^{\prime }$。
  （b）计算接受概率

$$\alpha (x,x^{\prime })=min\{1,\frac{p(x^{\prime })q(x^{\prime },x)}{p(x)q(x,x^{\prime })}\}$$

  （c）从区间$(0,1)$中按均匀分布随机抽取一个数$u$。
     若 $u⩽\alpha (x,x^{\prime })$，则状态 $x_i=x^{\prime }$；否则，状态 $x_i=x$。
（3）得到样本集合 $ { x_{m+1}, x_{m+2}, \cdots, x_n }$
计算

$$f_{mn}=\frac{1}{n-m}\sum _{i=m+1}^{n}f(x_i)$$

2. 理解单分量 Metropolis-Hastings 算法的基本思想

  根据书中第19.4.3节的单分量Metropolis-Hastings算法：

  在 Metropolis-Hastings 算法中，通常需要对多元变量分布进行抽样，有时对多元变量分布的抽样是困难的。可以对多元变量的每一变量的条件分布依次分别进行抽样，从而实现对整个多元变量的一次抽样, 这就是单分量 Metropolis-Hastings 算法。
  假设马尔可夫链的状态由 $k$ 维随机变量表示

$$x=(x_1,x_2,\cdots ,x_k{)}^T$$

其中 $x_j$ 表示随机变量 $x$ 的第 $j$ 个分量，$j=1,2,\cdots ,k$，而 $x^{(i)}$ 表示马尔可夫链在时刻 $i$ 的状态

$$x^{(i)}=(x_1^{(i)},x_2^{(i)},\cdots ,x_k^{(i)}{)}^T,i=1,2,\cdots ,n$$

其中 $x_j^{(i)}$ 是随机变量 $x^{(i)}$ 的第 $j$ 个分量，$j=1,2,\cdots ,k$。
  为了生成容量为 $n$ 的样本集合 $\{x^{(1)},x^{(2)},\cdots ,x^{(n)}\}$，单分量 Metropolis-Hastings 算法由下面的 $k$ 步迭代实现 Metropolis-Hastings 算法的一次迭代。
  设在第 $(i-1)$ 次迭代结束时分量 $x_j$ 的取值为 $x_j^{(i-1)}$，在第 $i$ 次迭代的第 $j$ 步，对分量 $x_j$ 根据 Metropolis-Hastings 算法更新，得到其新的取值 $x_j^{(i)}$。首先，由建议分布 $q(x_j^{(i-1)},x_j|x_{-j}^{(i)})$ 抽样产生分量 $x_j$ 的候选值 $x{{}^{\prime }}_j^{(i)}$，这里 $x_{-j}^{(i)}$ 表示在第 $i$ 次迭代的第 $(j-1)$ 步后的 $x^{(i)}$ 除去 $x_j^{(i-1)}$ 的所有值，即

$$x_{-j}^{(i)}=(x_1^{(i)},\cdots ,x_{j-1}^{(i)},x_{j+1}^{(i-1)},\cdots ,x_k^{(i-1)}{)}^T$$

其中分量 $1,2,\cdots ,j-1$ 已经更新。然后，按照接受概率

$$\alpha (x_j^{(i-1)},x{{}^{\prime }}_j^{(i)}|x_{-j}^{(i)})=min\{1,\frac{p(x{{}^{\prime }}_j^{(i)}|x_{-j}^{(i)})q(x{{}^{\prime }}_j^{(i)},x_j^{(i-1)}|x_{-j}^{(i)})}{p(x_j^{(i-1)}|x_{-j}^{(i)})q(x_j^{(i-1)},x{{}^{\prime }}_j^{(i)}|x_{-j}^{(i)})}\}$$

抽样决定是否接受候选值 $x{{}^{\prime }}_j^{(i)}$ 。如果 $x{{}^{\prime }}_j^{(i)}$ 被接受，则令 $x_j^{(i)}=x{{}^{\prime }}_j^{(i)}$；否则令 $x_j^{(i)}=x_j^{(i-1)}$。其余分量在第 $j$ 步不改变。马尔可夫链的转移概率为

$$p(x_j^{(i-1)},x{{}^{\prime }}_j^{(i)}|x_{-j}^{(i)})=\alpha (x_j^{(i-1)},x{{}^{\prime }}_j^{(i)}|x_{-j}^{(i)})q(x_j^{(i-1)},x{{}^{\prime }}_j^{(i)}|x_{-j}^{(i)})$$

3. 推导单分量 Metropolis-Hastings 算法

单分量 Metropolis-Hastings 算法
输入：抽样的目标分布的密度函数 $p(x)$，函数 $f(x)$，其中 $x={(x_1,x_2,\cdots ,x_k)}^T$；
输出：$p(x)$ 的随机样本 $\{x^{(m+1)},x^{(m+2)},\cdots ,x^{(n)}\}$，函数样本均值 $f_{mn}$；
参数：收敛步数 $m$, 迭代步数 $n$。
（1）任意选择一个初始值 $x_0$
（2）对 $i=1,2,\cdots ,n$ 循环执行
  设在第 $(i-1)$ 次迭代结束时分量 $x_j$ 的取值为 $x_j^{(i-1)}$
  （a）对 $j=1,2,\cdots ,k$ 循环执行
    （i）在第 $i$ 次迭代的第 $j$ 步，由建议分布 $q(x_j^{(i-1)},x_j|x_{-j}^{(i)})$ 抽样产生分量 $x_j$ 的候选值 $x{{}^{\prime }}_j^{(i)}$，
        这里 $x_{-j}^{(i)}$ 表示在第 $i$ 次迭代的第 $(j-1)$ 步后的 $x^{(i)}$ 除去 $x_j^{(i-1)}$ 的所有值，即

$$x_{-j}^{(i)}=(x_1^{(i)},\cdots ,x_{j-1}^{(i)},x_{j+1}^{(i-1)},\cdots ,x_k^{(i-1)}{)}^T$$

    （ii）计算接受概率

$$\alpha (x_j^{(i-1)},x{{}^{\prime }}_j^{(i)}|x_{-j}^{(i)})=min\{1,\frac{p(x{{}^{\prime }}_j^{(i)}|x_{-j}^{(i)})q(x{{}^{\prime }}_j^{(i)},x_j^{(i-1)}|x_{-j}^{(i)})}{p(x_j^{(i-1)}|x_{-j}^{(i)})q(x_j^{(i-1)},x{{}^{\prime }}_j^{(i)}|x_{-j}^{(i)})}\}$$

    （iii）从区间 $(0,1)$ 中按均匀分布随机抽取一个数 $u$。
        若 $u⩽\alpha (x_j^{(i-1)},x{{}^{\prime }}_j^{(i)}|x_{-j}^{(i)})$，则状态 $x_j^{(i)}=x{{}^{\prime }}_j^{(i)}$；否则，状态 $x_j^{(i)}=x_j^{(i-1)}$。
（3）得到样本集合 $\{x^{(m+1)},x^{(m+2)},\cdots ,x^{(n)}\}$
计算

$$f_{mn}=\frac{1}{n-m}\sum _{i=m+1}^{n}f(x^{(i)})$$

习题19.7

  假设进行伯努利实验，后验概率为 $P(\theta |y)$，其中变量 $y\in \{0,1\}$ 表示实验可能的结果，变量 $\theta$ 表示结果为 1 的概率。再假设先验概率 $P(\theta )$ 遵循 Beta 分布 $B(\alpha ,\beta )$，其中 $\alpha =1,\beta =1$；似然函数 $P(y|\theta )$ 遵循二项分布$ \text{Bin}(n, k, \theta)$，其中 $n=10,k=4$，即实验进行 10 次其中结果为 1 的次数为 4。试用 Metropolis-Hastings 算法求后验概率分布 $P(\theta |y)\propto P(\theta )P(y|\theta )$ 的均值和方差。（提示：可采用 Metropolis 选择，即假设建议分布是对称的。）

解答：

解题思路

1. 给出 Metropolis-Hastings 算法
2. 写出目标分布和建议分布
3. 自编程实现 Metropolis-Hastings 算法求解

解答步骤

第1步：Metropolis-Hastings 算法

  Metropolis-Hastings 算法的步骤详见书中第373~374页算法19.2。

第2步：写出目标分布和建议分布

  根据题意，可知后验概率 $P(\theta )\propto B(1,1)$，后验函数 $P(y|\theta )\propto \text{Bin}(10,4,\theta )$

  则后验概率分布

$$\begin{array}{rl}P(\theta |y)& \propto P(\theta )P(y|\theta )\\ & \propto B(1,1)\text{Bin}(10,4,\theta )\end{array}$$

  可取建议分布为 $B(1,1)$，接受分布为 $\text{Bin}(10,4,\theta )$

第3步：自编程实现 Metropolis-Hastings 算法求解

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import beta, binom


class MetropolisHastings:
    def __init__(self, proposal_dist, accepted_dist, m=1e4, n=1e5):
        """
        Metropolis Hastings

        :param proposal_dist: 建议分布
        :param accepted_dist: 接受分布
        :param m: 收敛步数
        :param n: 迭代步数
        """
        self.proposal_dist = proposal_dist
        self.accepted_dist = accepted_dist
        self.m = m
        self.n = n

    @staticmethod
    def __calc_acceptance_ratio(q, p, x, x_prime):
        """
        计算接受概率

        :param q: 建议分布
        :param p: 接受分布
        :param x: 上一状态
        :param x_prime: 候选状态
        """
        prob_1 = p.prob(x_prime) * q.joint_prob(x_prime, x)
        prob_2 = p.prob(x) * q.joint_prob(x, x_prime)
        alpha = np.min((1., prob_1 / prob_2))
        return alpha

    def solve(self):
        """
        Metropolis Hastings 算法求解
        """
        all_samples = np.zeros(self.n)
        # (1) 任意选择一个初始值
        x_0 = np.random.random()
        for i in range(int(self.n)):
            x = x_0 if i == 0 else all_samples[i - 1]
            # (2.a) 从建议分布中抽样选取
            x_prime = self.proposal_dist.sample()
            # (2.b) 计算接受概率
            alpha = self.__calc_acceptance_ratio(self.proposal_dist, self.accepted_dist, x, x_prime)
            # (2.c) 从区间 (0,1) 中按均匀分布随机抽取一个数 u
            u = np.random.uniform(0, 1)
            # 根据 u <= alpha，选择 x 或 x_prime 进行赋值
            if u <= alpha:
                all_samples[i] = x_prime
            else:
                all_samples[i] = x

        # (3) 随机样本集合
        samples = all_samples[self.m:]
        # 函数样本均值
        dist_mean = samples.mean()
        # 函数样本方差
        dist_var = samples.var()
        return samples[self.m:], dist_mean, dist_var

    @staticmethod
    def visualize(samples, bins=50):
        """
        可视化展示
        :param samples: 抽取的随机样本集合
        :param bins: 频率直方图的分组个数
        """
        fig, ax = plt.subplots()
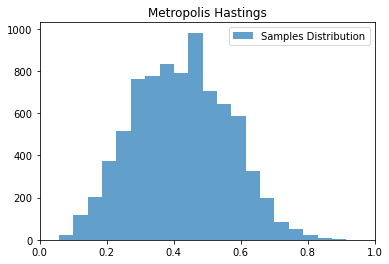
        ax.set_title('Metropolis Hastings')
        ax.hist(samples, bins, alpha=0.7, label='Samples Distribution')
        ax.set_xlim(0, 1)
        ax.legend()
        plt.show()

class ProposalDistribution:
    """
    建议分布
    """

    @staticmethod
    def sample():
        """
        从建议分布中抽取一个样本
        """
        # B(1,1)
        return beta.rvs(1, 1, size=1)

    @staticmethod
    def prob(x):
        """
        P(X = x) 的概率
        """
        return beta.pdf(x, 1, 1)

    def joint_prob(self, x_1, x_2):
        """
        P(X = x_1, Y = x_2) 的联合概率
        """
        return self.prob(x_1) * self.prob(x_2)

class AcceptedDistribution:
    """
    接受分布
    """

    @staticmethod
    def prob(x):
        """
        P(X = x) 的概率
        """
        # Bin(4, 10)
        return binom.pmf(4, 10, x)

import warnings
warnings.filterwarnings("ignore")

# 收敛步数
m = 1000
# 迭代步数
n = 10000

# 建议分布
proposal_dist = ProposalDistribution()
# 接受分布
accepted_dist = AcceptedDistribution()

metropolis_hastings = MetropolisHastings(proposal_dist, accepted_dist, m, n)

# 使用 Metropolis-Hastings 算法进行求解
samples, dist_mean, dist_var = metropolis_hastings.solve()
print("均值:", dist_mean)
print("方差:", dist_var)

# 对结果进行可视化
metropolis_hastings.visualize(samples, bins=20)

均值: 0.4214185307283342
方差: 0.019466091658555083

习题19.8

  设某试验可能有五种结果，其出现的概率分别为

$$\frac{\theta }{4}+\frac{1}{8},\frac{\theta }{4},\frac{\eta }{4},\frac{\eta }{4}+\frac{3}{8},\frac{1}{2}(1-\theta -\eta )$$

模型含有两个参数 $\theta$ 和 $\eta$，都介于 0 和 1 之间。现有 22 次试验结果的观测值为

$$y=(y_1,y_2,y_3,y_4,y_5)=(14,1,1,1,5)$$

其中 $y_i$ 表示 22 次试验中第 $i$ 个结果出现的次数，$i=1,2,\cdots ,5$。试用吉布斯抽样估计参数 $\theta$ 和 $\eta$ 的均值和方差。

解答

解题思路

1. 给出吉布斯抽样算法
2. 定义目标概率的密度函数和各参数的满条件分布
3. 自编程实现吉布斯抽样算法进行求解

解答步骤

第1步：吉布斯抽样算法

  根据书中第19.5.2节的吉布斯抽样算法的描述：

算法19.3(吉布斯抽样)
输入：目标概率分布的密度函数 $p(x)$，函数 $f(x)$；
输出：$p(x)$ 的随机样本 $x_{m+1},x_{m+2},\cdots ,x_n$，函数样本均值 $f_{mn}$；
参数：收敛步数 $m$，迭代步数 $n$。
（1）初始化。给出初始样本 $x^{(0)}={(x_1^{(0)},x_2^{(0)},\cdots ,x_k^{(0)})}^T$。
（2）对 $i$ 循环执行
设第 $(i-1)$ 次迭代结束时的样本为 $x^{(i-1)}={(x_1^{(i-1)},x_2^{(i-1)},\cdots ,x_k^{(i-1)})}^T$，则第 $i$ 次迭代进行如下几步操作：

$$\{\begin{array}{l}\text{(1) 由满条件分布 }p(x_1|x_2^{(i-1)},\cdots ,x_k^{(i-1)})\text{ 抽取 }{x}_1^{(i)}\\ ⋮\\ \text{(j) 由满条件分布 }p(x_j|x_1^{(i)},\cdots ,x_{j-1}^{(i)},x_{j+1}^{(i-1)},\cdots ,x_k^{(i-1)})\text{ 抽取 }{x}_j^{(i)}\\ ⋮\\ \text{(k) 由满条件分布 }p(x_k|x_1^{(i)},\cdots ,x_{k-1}^{(i)})\text{ 抽取 }{x}_k^{(i)}\end{array}$$

得到第 $i$ 次迭代值 $x^{(i)}={(x_1^{(i)},x_2^{(i)},\cdots ,x_k^{(i)})}^T$。
（3）得到样本集合

$$\{x^{(m+1)},x^{(m+2)},\cdots ,x^{(n)}\}$$

（4）计算

$$f_{mn}=\frac{1}{n-m}\sum _{i=m+1}^{n}f(x^{(i)})$$

第2步：定义目标概率的密度函数和各参数的满条件分布

  根据题意，可知目标概率的分布函数为

$$\begin{array}{rl}P& =(p_1,p_2,p_3,p_4,p_5)\\ & =(\frac{\theta }{4}+\frac{1}{8},\frac{\theta }{4},\frac{\eta }{4},\frac{\eta }{4}+\frac{3}{8},\frac{1}{2}(1-\theta -\eta ))\end{array}$$

  可得：

$$\begin{array}{l}{\displaystyle \frac{\theta }{4}+\frac{1}{8}>0}\\ {\displaystyle \frac{\theta }{4}>0}\\ {\displaystyle \frac{\eta }{4}>0}\\ {\displaystyle \frac{\eta }{4}+\frac{3}{8}>0}\\ {\displaystyle \frac{1}{2}(1-\theta -\eta )>0}\\ {\displaystyle \frac{\theta }{4}+\frac{1}{8}+\frac{\theta }{4}+\frac{\eta }{4}+\frac{\eta }{4}+\frac{3}{8}+\frac{1}{2}(1-\theta -\eta )=1}\\ 0<\theta <1\\ 0<\eta <1\end{array}$$

  求解得到：

$$\begin{array}{l}\theta +\eta <1\\ 0<\theta <1\\ 0<\eta <1\end{array}$$

  则参数 $\theta$ 和 $\eta$ 的满分布条件概率为

$$\begin{gathered} P(\theta |y,\eta )=({(\frac{\theta }{4}+\frac{1}{8})}^{14},\frac{\theta }{4},\frac{\eta }{4},\frac{\eta }{4}+\frac{3}{8},{(\frac{1}{2}(1-\theta -\eta ))}^5),\theta \in (0,1-\eta ) \\ P(\eta |y,\theta )=({(\frac{\theta }{4}+\frac{1}{8})}^{14},\frac{\theta }{4},\frac{\eta }{4},\frac{\eta }{4}+\frac{3}{8},{(\frac{1}{2}(1-\theta -\eta ))}^5),\eta \in (0,1-\theta ) \end{gathered}$$

第2步：编程实现吉布斯抽样算法进行求解

import matplotlib.pyplot as plt
import numpy as np


class GibbsSampling:
    def __init__(self, target_dist, j, m=1e4, n=1e5):
        """
        Gibbs Sampling 算法

        :param target_dist: 目标分布
        :param j: 变量维度
        :param m: 收敛步数
        :param n: 迭代步数
        """
        self.target_dist = target_dist
        self.j = j
        self.m = int(m)
        self.n = int(n)

    def solve(self):
        """
        Gibbs Sampling 算法求解
        """
        # (1) 初始化
        all_samples = np.zeros((self.n, self.j))
        # 任意选择一个初始值
        x_0 = np.random.random(self.j)
        # x_0 = np.array([0.5, 0.5])
        # (2) 循环执行
        for i in range(self.n):
            x = x_0 if i == 0 else all_samples[i - 1]
            # 满条件分布抽取
            for k in range(self.j):
                x[k] = self.target_dist.sample(x, k)
            all_samples[i] = x
        # (3) 得到样本集合
        samples = all_samples[self.m:]
        # (4) 计算函数样本均值
        dist_mean = samples.mean(0)
        dist_var = samples.var(0)
        return samples[self.m:], dist_mean, dist_var

    @staticmethod
    def visualize(samples, bins=50):
        """
        可视化展示
        :param samples: 抽取的随机样本集合
        :param bins: 频率直方图的分组个数
        """
        fig, ax = plt.subplots()
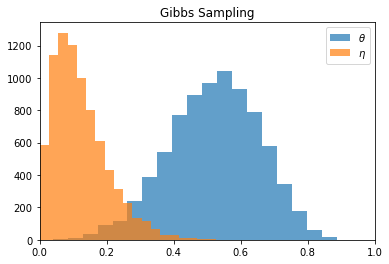
        ax.set_title('Gibbs Sampling')
        ax.hist(samples[:, 0], bins, alpha=0.7, label='$\\theta$')
        ax.hist(samples[:, 1], bins, alpha=0.7, label='$\\eta$')
        ax.set_xlim(0, 1)
        ax.legend()
        plt.show()

class TargetDistribution:
    """
    目标概率分布
    """

    def __init__(self):
        # 联合概率值过小，可对建议分布进行放缩
        self.c = self.__select_prob_scaler()

    def sample(self, x, k=0):
        """
        使用接受-拒绝方法从满条件分布中抽取新的分量 x_k
        """
        theta, eta = x
        if k == 0:
            while True:
                new_theta = np.random.uniform(0, 1 - eta)
                alpha = np.random.uniform()
                if (alpha * self.c) < self.__prob([new_theta, eta]):
                    return new_theta
        elif k == 1:
            while True:
                new_eta = np.random.uniform(0, 1 - theta)
                alpha = np.random.uniform()
                if (alpha * self.c) < self.__prob([theta, new_eta]):
                    return new_eta

    def __select_prob_scaler(self):
        """
        选择合适的建议分布放缩尺度
        """
        prob_list = []
        step = 1e-3
        for theta in np.arange(step, 1, step):
            for eta in np.arange(step, 1 - theta + step, step):
                prob = self.__prob((theta, eta))
                prob_list.append(prob)
        searched_max_prob = max(prob_list)
        upper_bound_prob = searched_max_prob * 10
        return upper_bound_prob

    @staticmethod
    def __prob(x):
        """
        P(X = x) 的概率
        """
        theta = x[0]
        eta = x[1]
        p1 = (theta / 4 + 1 / 8) ** 14
        p2 = theta / 4
        p3 = eta / 4
        p4 = (eta / 4 + 3 / 8)
        p5 = 1 / 2 * (1 - theta - eta) ** 5
        p = (p1 * p2 * p3 * p4 * p5)
        return p

# 收敛步数
m = 1e3
# 迭代步数
n = 1e4

# 目标分布
target_dist = TargetDistribution()

# 使用 Gibbs Sampling 算法进行求解
gibbs_sampling = GibbsSampling(target_dist, 2, m, n)

samples, dist_mean, dist_var = gibbs_sampling.solve()

print(f'theta均值：{dist_mean[0]}, theta方差：{dist_var[0]}')
print(f'eta均值：{dist_mean[1]}, eta方差：{dist_var[1]}')

# 对结果进行可视化
GibbsSampling.visualize(samples, bins=20)

theta均值：0.5200493163002229, theta方差：0.018093366768230302
eta均值：0.12315468306475189, eta方差：0.006544978550617504