2.1.3. Swing 算法

当你在电商平台购买了一件T恤后，系统会向你推荐什么？如果是其他款式的T恤，这属于替代性推荐；如果是配套的裤子或配饰，这就是互补性推荐。传统的Item-based协同过滤在处理这类细粒度的商品关系时往往力不从心——它将所有用户-物品交互一视同仁，无论是用户深思熟虑的购买，还是偶然的误点击、好奇心驱动的浏览，都被赋予相同的权重。这种做法不仅难以区分真正的兴趣关联和随机噪声，更无法有效捕捉物品间的替代性与互补性关系。

图2.1.3 产品之间的替代性和互补性关系

Swing Score (Yang et al., 2020) 提供了一个新的解题思路。它不再简单地统计共同购买次数，而是深入分析用户-物品二部图中的内部子结构，通过捕捉那些在用户行为中反复出现、具备较强“鲁棒性”的共同购买关系来度量物品相似性。其核心洞察是：如果多个用户在其他共同购买行为较少的情况下，同时购买了同一对物品，那么这对物品之间的关联性就更可信。

基于这一思想，Swing算法能够构建更准确的产品索引，并在此基础上衍生出Surprise算法来专门处理互补商品推荐的挑战。

Swing算法的实现可以分为两个主要步骤：先构建用户-物品二部图，再通过分析图中用户对的共同交互模式（即swing结构）来计算物品相似度。

用户-物品二部图构建

我们首先将用户与物品的交互数据转化为一个二部图。在这个图中，一边是所有用户节点，另一边是所有物品节点。如果用户对某个物品发生了点击、购买等行为，就在对应的用户节点与物品节点之间添加一条边。这个二部图为后续的相似度计算提供了结构化的数据基础。

物品相似度计算

构建好二部图后，我们来计算任意一对物品 \(i\) 与 \(j\) 的相似度。设 \(U_i\) 和 \(U_j\) 分别表示与物品 \(i\) 和 \(j\) 有过交互的用户集合，\(I_u\) 表示用户 \(u\) 交互过的所有物品集合。

具体计算过程如下：

用户交集提取：首先找到同时与物品 \(i\) 和 \(j\) 相连的用户集合 \(U_i \cap U_j\)。

内部子结构分析：对集合中的每一对用户 \((u, v)\)，统计他们的其他共同购买行为。如果用户 \(u\) 与 \(v\) 的其他交互行为重合较少（即 \(|I_u \cap I_v|\) 较小），则认为他们在共同选择物品 \(i\) 和 \(j\) 上的行为更具特异性，应该为这对物品贡献更高的相似度得分。

Swing score 的基础计算公式为：

(2.1.14)\[s(i, j) = \sum_{u \in U_i \cap U_j} \sum_{v \in U_i \cap U_j} \frac{1}{\alpha + |I_u \cap I_v|}\]

其中，\(\alpha\) 是平滑系数，用来防止分母过小导致数值不稳定。

让我们通过一个具体例子来理解这个公式。如 图2.1.4 所示，红色边连接的子图表示一个swing结构。用户A和B有四个swing结构，分别是 \([A, h, B]\)、\([A, t, B]\)、\([A, r, B]\)、\([A, p, B]\)。

图2.1.4 Swing Score 计算示意图

假设 \(\alpha = 1\)，那么：

• 用户对 \([A, B]\) 的贡献分数为：\(\frac{1}{1 + 4} = \frac{1}{5}\)

• 用户对 \([B, C]\) 的贡献分数为：\(\frac{1}{1 + 2} = \frac{1}{3}\)

• 用户对 \([A, C]\) 的贡献分数为：\(\frac{1}{1 + 2} = \frac{1}{3}\)

因此，物品h和p之间的swing score为：\(s(h, p) = \frac{1}{5} + \frac{1}{3} + \frac{1}{3} = \frac{13}{15}\)，而物品h和t（或r）之间的swing score为：\(s(h, t) = s(h, r) = \frac{1}{3}\)。

用户权重调整：为了降低活跃用户对计算结果的过度影响，我们引入用户权重 \(w_u = \frac{1}{\sqrt{|I_u|}}\)。最终的物品相似度计算公式为：

(2.1.15)\[s(i, j) = \sum_{u \in U_i \cap U_j} \sum_{v \in U_i \cap U_j} w_u \cdot w_v \cdot \frac{1}{\alpha + |I_u \cap I_v|}\]

这个公式能够精准刻画物品之间的关联强度，为推荐系统提供更可靠的相似度度量。

2.1.3.1. Surprise 算法：互补商品推荐的进阶方案

虽然Swing Score已经能够有效捕捉物品间的关联关系，但在处理互补商品推荐时仍面临挑战。相比替代关系，互补关系具有明确的时序性和方向性——用户通常先购买主商品，再购买配套商品（如先买手机再买手机壳）。为了更好地挖掘这类关系，Swing论文基于Swing Score提出了Surprise算法。

Surprise算法的设计基于一个重要观察：真正的互补关系主要发生在不同商品类别之间，且购买时间间隔越短，互补性越强。同时，为了解决用户共购数据稀疏的问题，该算法通过商品聚类将稀疏的商品级别共现信号聚合到聚类级别，从而获得更可靠的互补关系证据。

Surprise算法从类别、商品和聚类三个层面来衡量互补相关性：

类别层面

在这一层面，我们利用商品与类别之间的映射关系构建user-category矩阵。基于这个矩阵，可以计算类别 \(i\) 与类别 \(j\) 之间的相关性：

(2.1.16)\[\theta_{i,j} = p(c_{i,j} \mid c_j) = \frac{N(c_{i,j})}{N(c_j)}\]

其中，\(N(c_{i,j})\) 表示先购买类别 \(i\) 后又购买类别 \(j\) 这一事件发生的次数，\(N(c_j)\) 表示购买类别 \(j\) 的次数。考虑到不同类别的数量差异，我们采用最大相对落点作为划分阈值来筛选相关类别。

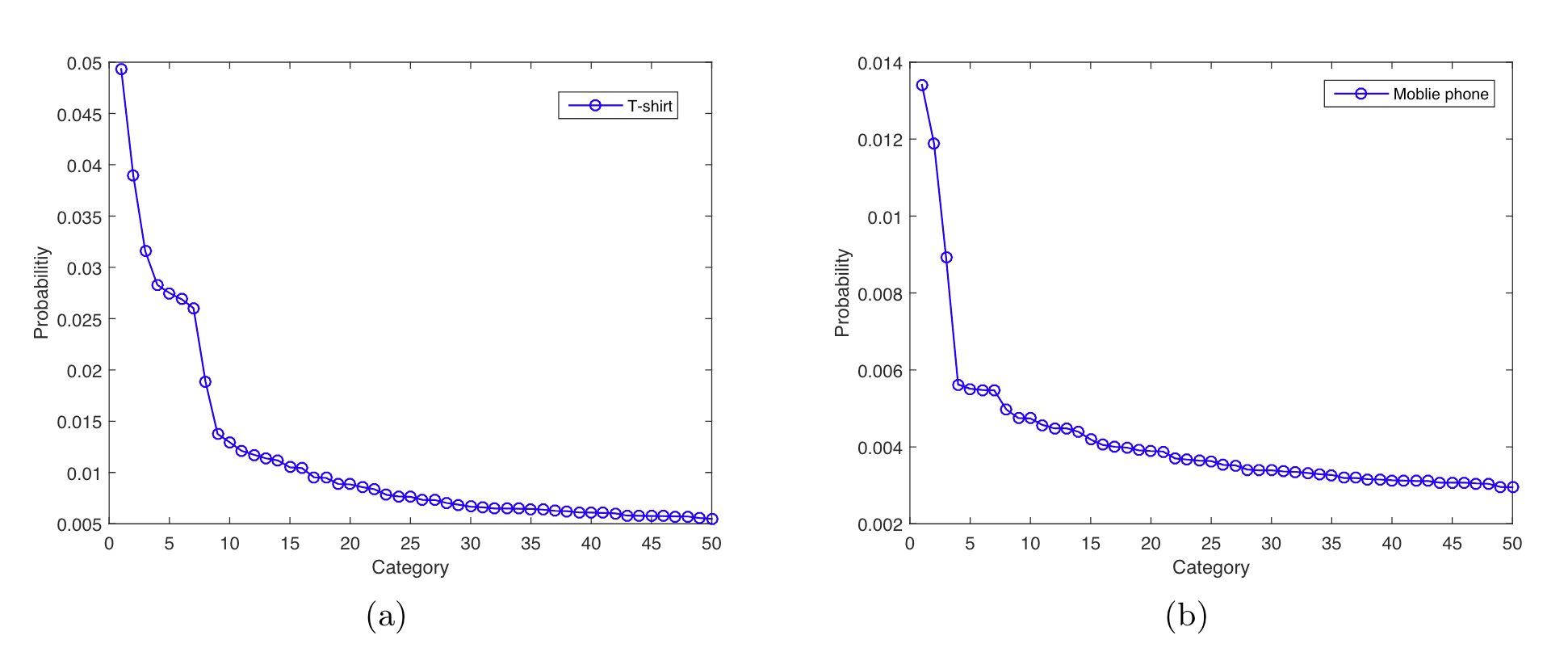
图2.1.5 最大相对落点示意图

例如，图(a)中T恤类选取了前八个相关类别，而图(b)中手机类选择了前三个相关类别。

商品层面

针对类别相关的商品对，Surprise算法重点考虑两个因素：购买顺序的重要性（如先买手机后买充电宝比反之更合理）以及时间间隔的影响（间隔越短，互补性越强）。

商品层面的互补相关性计算公式为：

(2.1.17)\[s_{1}(i, j) = \frac{\sum_{u \in U_i \cap U_j} \frac{1}{1 + \left| t_{ui} - t_{uj} \right|}}{\lVert U_i \rVert \times \lVert U_j \rVert}\]

其中，\(t_{ui}\) 和 \(t_{uj}\) 分别表示用户 \(u\) 购买物品 \(i\) 和 \(j\) 的时间，且只有当 \(j\) 属于 \(i\) 的相关类别且购买时间晚于 \(i\) 时才计入计算。

聚类层面

考虑到实际业务中商品数量可能达到数十亿的规模，传统聚类算法难以胜任。Surprise算法采用标签传播算法 (Raghavan et al., 2007) 在大规模Item-Item图上进行聚类，这里的邻居关系通过Swing算法计算，边权重即为Swing分数。

这种方法不仅高效（通常15分钟内可对数十亿商品完成聚类），还能显著缓解数据稀疏问题。设 \(L(i)\) 表示商品 \(i\) 的聚类标签，则聚类层面的相似度可以表示为：

(2.1.18)\[s_2(i,j) = s_1(L(i), L(j))\]

线性组合

最终，Surprise算法采用线性组合的方式融合不同层面的信息：

(2.1.19)\[s(i, j) = \omega \cdot s_{1}(i, j) + (1 - \omega) \cdot s_{2}(i, j)\]

其中，\(\omega\) 是权重超参数，\(s_{2}(i, j)\) 代表聚类层面的互补相关性。

通过这种多层次的综合分析，Surprise算法成功拓展了Swing Score的应用范围，为互补商品推荐提供了一套系统而高效的解决方案。该方法不仅利用了类别信息和标签传播技术有效解决了数据稀疏问题，还能够准确捕捉商品间的时序和方向性关系，从而提升推荐系统的整体效果。

2.1.3.2. 代码实践

首先，我们导入funrec库中的核心组件：

import sys

import funrec

Swing算法的核心在于Swing Score的计算，它通过分析用户-物品二部图中的swing结构来度量物品相似度：

def calculate_swing_similarity(item_users, user_items, user_weights, item_i, item_j, alpha=1.0):
    """
    计算两个物品之间的Swing Score相似度
    参考funrec.models.swing.Swing._calculate_swing_similarity_optimized()的核心逻辑
    """
    # 找到同时与物品i和j交互的用户（共同用户）
    common_users = item_users[item_i].intersection(item_users[item_j])

    if len(common_users) < 2:
        return 0.0  # 至少需要2个共同用户才能计算Swing score

    swing_score = 0.0
    common_users_list = list(common_users)

    # 计算所有共同用户对的贡献
    for u in common_users_list:
        for v in common_users_list:
            if u == v:
                continue

            # 找到用户u和v的共同交互物品
            common_items_uv = user_items[u].intersection(user_items[v])

            # 使用预计算的用户权重
            user_weight_u = user_weights[u]  # 1.0 / sqrt(|I_u|)
            user_weight_v = user_weights[v]  # 1.0 / sqrt(|I_v|)

            # Swing Score核心公式
            contribution = (user_weight_u * user_weight_v) / (alpha + len(common_items_uv))
            swing_score += contribution

    return swing_score

构建、训练和评估Swing算法：

import os
import sys
import funrec
from funrec.utils import build_metrics_table

# 加载配置
config = funrec.load_config('swing')

# 加载数据
train_data, test_data = funrec.load_data(config.data)

# 准备特征
feature_columns, processed_data = funrec.prepare_features(config.features, train_data, test_data)

# 训练模型
models = funrec.train_model(config.training, feature_columns, processed_data)

# 评估模型
metrics = funrec.evaluate_model(models, processed_data, config.evaluation, feature_columns)

print(build_metrics_table(metrics))

+---------------+--------------+----------------+---------------+
|   hit_rate@10 |   hit_rate@5 |   precision@10 |   precision@5 |
+===============+==============+================+===============+
|        0.6194 |       0.5042 |         0.1282 |        0.1629 |
+---------------+--------------+----------------+---------------+