3.5.1. 多塔结构

在多目标建模领域，如 MMoE 所展现的那样，专家网络（Expert）用于挖掘不同任务之间共享的底层特征表示，而门控网络（Gate）则动态分配专家权重，根据不同任务的特性需求进行适配。这种由 “共享专家 + 任务专属门控” 构成的架构，具备了同时捕捉共性（共享专家所提取的通用特征）与特性（门控网络赋予的特定权重）的能力。

多场景建模与多任务学习类似但关注点不同：多任务学习处理相同场景/分布下的不同任务（如单样本同时预估CTR、CVR），而多场景建模处理不同场景/分布下的相同任务（如不同场景预估相同CTR）。前者是对于一条样本预估多个不同的目标值，后者是对于不同的样本预估相同的目标值。多场景建模若采用独立模型，会忽视场景共性，导致小场景效果差且资源消耗剧增；若混合样本训练单一模型，则会忽视场景差异，降低预测精度。

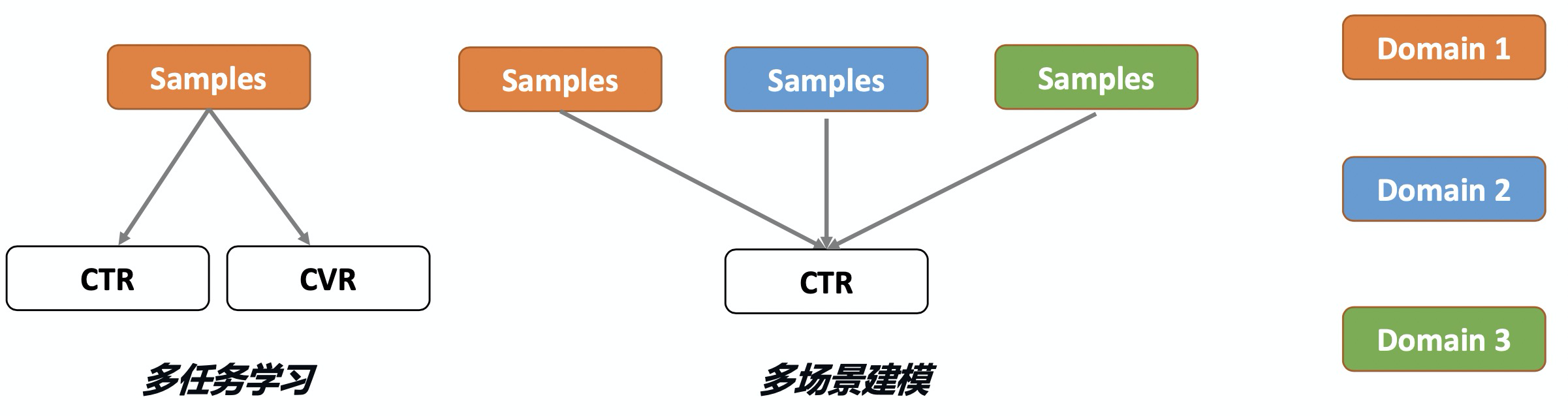
图3.5.1 多目标与多场景建模的差异(图片来自阿里妈妈博客)

本小节将会介绍基于多塔结构建模时，在利用多场景共性的前提下，显式地使用不同场景的信号来捕捉场景的特性。

3.5.1.1. HMoE

在多任务建模小节中，介绍了MMoE（Mixture-of-Experts）底层通过多专家网络作为多任务的共享特征，顶层对于不同的任务使用门控机制融合专家特征实现不同任务差异化的学习。在多场景建模中HMoE (Li et al., 2020) 借鉴了MMoE的思路，底层同样适用多专家网络提取提取多个场景的特征作为共享特征，只不过顶层的多个塔不再是多个任务的输出，而是多个场景的输出，HMoE模型结构如下：

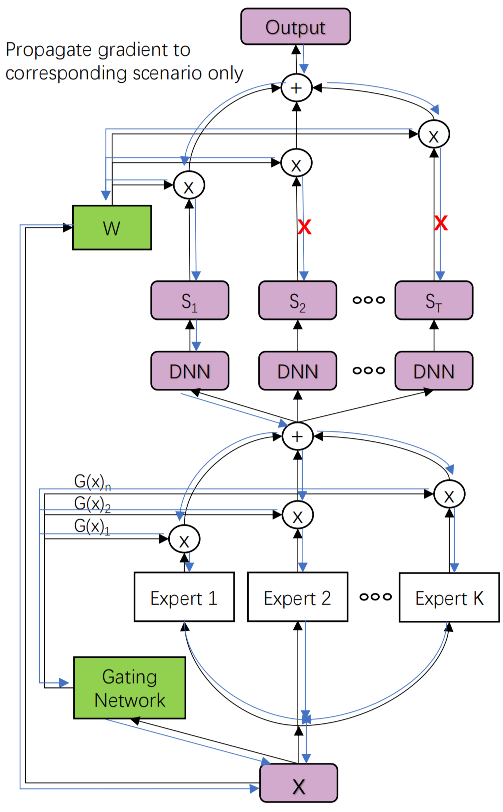
图3.5.2 HMoE模型结构

模型的底层使用多个专家抽取多个场景的特征，并通过一组门控网络将多个专家的输出结果进行融合，最后输入给上层不同的场景塔。

(3.5.1)\[M(x) = \sum_{i=1}^{K} G_i(x) E_i(x)\]

原论文中是对于所有场景的塔都使用同一组门控融合后的专家特征，这种方式可以看成是多任务建模中的Shared-Bottom式的特征共享，只不过以多个FCN的融合输出替代了单个FCN的输出。从MMoE的经验来看，如果多个任务之间的相关性较差，底层这种特征硬共享可能会出现负迁移的现象。所以这种方式也不一定就是多场景建模的最优方案，也可以尝试对于不同的场景，使用不同门控融合后的专家特征。如第\(t\)个场景的输入特征表示为\(M_t(x) = \sum_{i=1}^{K} G_i^t(x) E_i(x)\)，最终哪种效果更好可以根据自己的场景做实验得到。

在得到了底层多场景特征之后，模型单场景的最终预估值不是简单的直接使用对应场景Tower打分，而是将多个场景输出打分融合为单个场景的打分。第\(t\)个场景的模型打分表示如下：

(3.5.2)\[out_t = \sum_{i=1}^{T} W_i(x) S_i(x)\]

其中\(W_i(x)\)是场景\(i\)的融合权重，原论文中对于不同的场景下打分融合的\(W\)是否共享也未明确说明，但可以根据MMoE的思路，给每个场景都学习一个融合的权重，即第\(t\)个场景的预估值可以表示为：\(out_t = \sum_{i=1}^{T} W_i^t(x) S_i(x)\)

从最终单场景由多个场景打分融合可以看出，对于某个场景\(t\)的样本，HMoE不仅需要计算它在场景\(t\)下的打分，还需要计算它在场景下的打分，计算场景\(t\)最终的打分时，其他场景的打分对\(t\)场景也是有参考价值的。

虽然在前向推理时可以将一条样本预估出不同场景的打分，但是对于某个场景\(t\)的样本来说应该只影响当前场景的参数（主要是场景塔的参数），否则\(a\)场景下的样本直接影响\(b\)场景的参数，很容易导致模型对于场景的感知下降，进而让整个多场景的模型效果变差。因此在计算融合打分时候，需要抑制其他场景打分的梯度回传，最终场景\(t\)的打分表示如下

(3.5.3)\[out_t(x) = W_t(x) S_t(x) + \sum_{j=1, j \neq t}^{T} W_j(x) \underbrace{S_j(x)}_{\text{stop gradient}}\]

不共享融合权重的打分公式为：\(out_t(x) = W_t^t(x) S_t(x) + \sum_{j=1, j \neq t}^{T} W_j^t(x) \underbrace{S_j(x)}_{\text{stop gradient}}\)

HMoE核心代码如下，其中包括了是否共享门控和融合打分权重的部分。

# 构建dnn的输入
dnn_inputs = concat_group_embedding(group_embedding_feature_dict, 'dnn')

# 创建多个专家
expert_output_list = [
    DNNs(shared_expert_dnn_units, name=f"expert_{i}")(dnn_inputs)
    for i in range(shared_expert_nums)
]
expert_concat = tf.keras.layers.Lambda(lambda x: tf.stack(x, axis=1))(expert_output_list)  # (None, expert_num, dims)

# 每域独立 Gate 融合专家输出
domain_tower_input_list = []
for i in range(num_domains):
    gate_output = DNNs(gate_dnn_units, name=f"gate_{i}")(dnn_inputs)
    gate_output = tf.keras.layers.Dense(shared_expert_nums, use_bias=False, activation='softmax', name=f"gate_{i}_softmax")(gate_output)
    gate_output = tf.keras.layers.Lambda(lambda x: tf.expand_dims(x, axis=-1))(gate_output)  # (None, expert_num, 1)
    gate_expert_output = tf.keras.layers.Lambda(lambda x: x[0] * x[1])([gate_output, expert_concat])
    gate_expert_output = tf.keras.layers.Lambda(lambda x: tf.reduce_sum(x, axis=1, keepdims=False))(gate_expert_output)
    domain_tower_input_list.append(gate_expert_output)

# 定义每个域的塔（Tower）
domain_tower_output_list = []
for i in range(num_domains):
    domain_dnn_input = domain_tower_input_list[i]
    task_output = DNNs(domain_tower_units, name=f"tower_{i}")(domain_dnn_input)
    domain_tower_output_list.append(task_output)

# 域间权重（参数化，可选预处理）
if domain_weight_units is not None:
    domain_weight_input = DNNs(domain_weight_units, name="domain_weight_dnn")(dnn_inputs)
else:
    domain_weight_input = dnn_inputs
domain_weight = tf.keras.layers.Dense(num_domains, activation='softmax', name="domain_weight")(domain_weight_input)  # (None, num_domains)

# 融合domain信息（own + cross with stop_gradient）
mixed_output_list = []
for i in range(num_domains):
    wi = tf.keras.layers.Lambda(lambda w: w[:, i:i+1])(domain_weight)
    weighted_output = tf.keras.layers.Lambda(lambda x: x[0] * x[1])([domain_tower_output_list[i], wi])
    for j in range(num_domains):
        if i == j:
            continue
        grad_output = tf.keras.layers.Lambda(lambda x: tf.stop_gradient(x))(domain_tower_output_list[j])
        wj = tf.keras.layers.Lambda(lambda w: w[:, j:j+1])(domain_weight)
        weighted_output = tf.keras.layers.Add()([
            weighted_output,
            tf.keras.layers.Multiply()([wj, grad_output])
        ])
    mixed_output_list.append(weighted_output)

# 将所有domain的数据拼接成batch并输出 logits
final_domain_output = tf.keras.layers.Concatenate(axis=0)(mixed_output_list)
dnn_logits = PredictLayer(activation=None, name="dnn_logits")(final_domain_output)

代码实践

from funrec import run_experiment

run_experiment('hmoe')

+--------+--------+------------+
|    auc |   gauc |   val_user |
+========+========+============+
| 0.5972 | 0.5471 |        217 |
+--------+--------+------------+

3.5.1.2. STAR

STAR（Star Topology Adaptive Recommender）:cite:sheng2021one 模型采用星型拓扑结构，实现场景私有参数和场景共享参数同时建模场景差异性和共性。场景私有参数以及场景共享参数最终聚合得到每个场景的模型。STAR结构如下图所示。

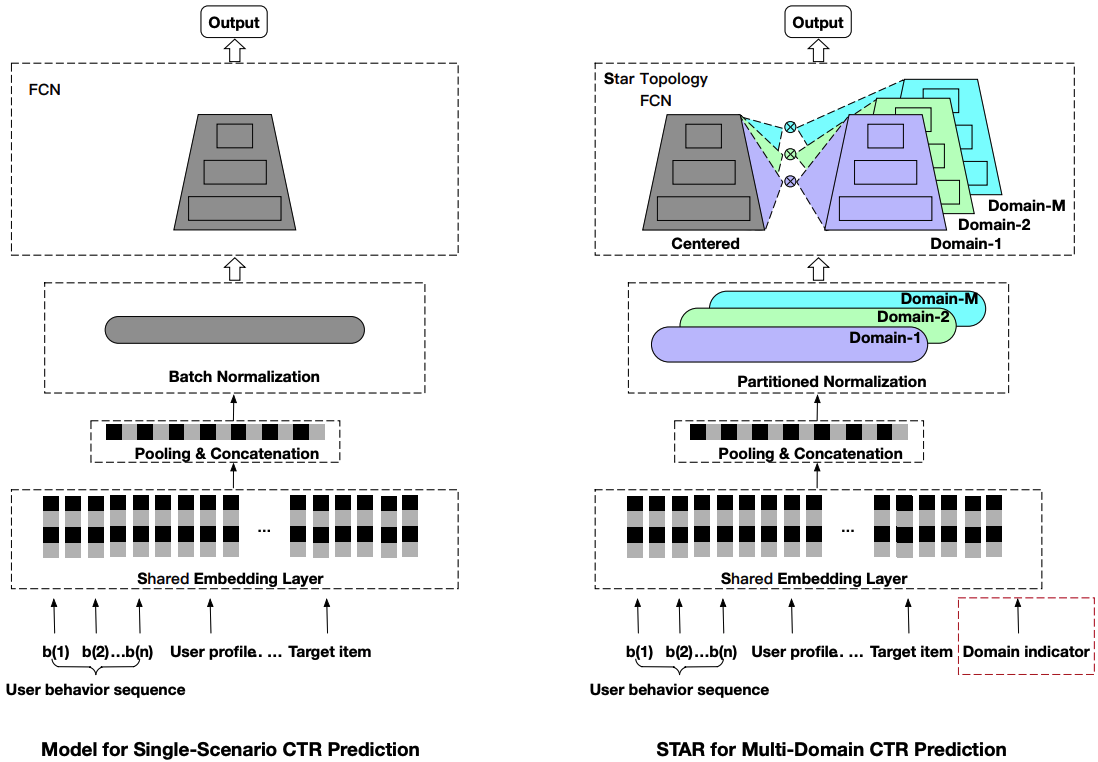
图3.5.3 STAR模型结构

相比于单场景的模型，STAR有三个针对多场景建模的创新思路值得学习，分别是星型拓扑结构的全连接网络（STAR Topology Fully-Connected Network），Partitioned Normalization 以及辅助网络，下面将以此进行介绍。

STAR Topology Fully-Connected Network

星形拓扑全连接结构的核心思想是对于每一个全连接网络（FCN）都有场景共享和场景独占的部分，每个场景最终的参数由共享和独占参数通过element-wise product融合计算得到。

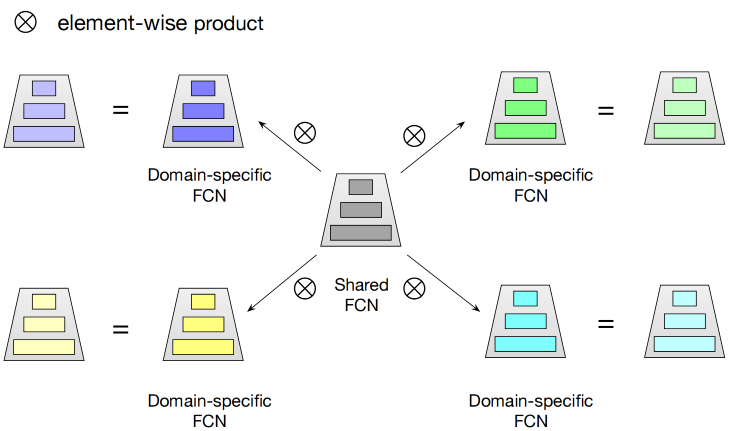
图3.5.4 STAR FCN结构

具体而言，对于第\(p\)个场景的FCN的最终参数\(W_p^{\star},b_p^{\star}\)表示如下：

(3.5.4)\[\begin{split}W_p^{\star} = W_p \otimes W \\ b_p^{\star} = b_p + b\end{split}\]

其中\(W_p,W\)分别表示第\(p\)个场景独有和全场景共享的参数，\(b_p,b\)也一样。

如果用\(in_p\)表示第\(p\)个场景FCN的输入，则该层星形FCN的输出\(out_p\)表示为：

(3.5.5)\[out_p = \phi((W_p^\star)^\top in_p + b_p^\star),\]

其中\(\phi\)是激活函数。

STAR Topology Fully-Connected Network的具体实现如下：

class StarTopologyFCN(tf.keras.layers.Layer):
    """
    星型拓扑 FCN（简化版）
    - 核心思想：中心共享参数 + 各域的轻量适配器（增量参数），
    """
    def __init__(self,
                 num_domain,
                 hidden_units,
                 activation="relu",
                 dropout=0.,
                 l2_reg=0.,
                 **kwargs):
        super(StarTopologyFCN, self).__init__( **kwargs)
        self.num_domain = num_domain
        self.hidden_units = list(hidden_units)
        self.activation = tf.keras.activations.get(activation)
        self.dropout = tf.keras.layers.Dropout(dropout)
        self.l2_reg = l2_reg

    def build(self, input_shape):
        # inputs 形状为 (x, domain_index)，这里只取特征 x 的维度
        input_shape = input_shape[0]
        input_dim = input_shape[-1]
        layer_dims = [input_dim] + self.hidden_units

        # 共享参数（星型中心）：每一层的共享权重 / 共享偏置
        self.shared_kernels = [
            self.add_weight(
                name=f"shared_kernel_{i}",
                shape=(layer_dims[i], layer_dims[i+1]),
                initializer="glorot_uniform",
                regularizer=tf.keras.regularizers.l2(self.l2_reg),
                trainable=True,
            ) for i in range(len(self.hidden_units))
        ]
        self.shared_biases = [
            self.add_weight(
                name=f"shared_bias_{i}",
                shape=(layer_dims[i+1],),
                initializer="zeros",
                trainable=True,
            ) for i in range(len(self.hidden_units))
        ]

        # 域适配器（辐射边）：用 Embedding 为每个域生成增量参数（kernel / bias）
        self.domain_kernel_embs = [
            tf.keras.layers.Embedding(
                self.num_domain,
                layer_dims[i] * layer_dims[i+1],
                embeddings_initializer="glorot_uniform",
                embeddings_regularizer=tf.keras.regularizers.l2(self.l2_reg),
            ) for i in range(len(self.hidden_units))
        ]
        self.domain_bias_embs = [
            tf.keras.layers.Embedding(
                self.num_domain,
                layer_dims[i+1],
                embeddings_initializer="zeros",
            ) for i in range(len(self.hidden_units))
        ]

    def call(self, inputs, training=None):
        # x: [B, Din]；domain_index: [B]
        x, domain_index = inputs
        for i in range(len(self.hidden_units)):
            # 取出域增量参数并重塑到矩阵形状
            delta_w = self.domain_kernel_embs[i](domain_index)                      # [B, Din*Dout]
            delta_w = tf.reshape(delta_w, (-1,) + self.shared_kernels[i].shape.as_list())  # [B, Din, Dout]
            # 星型融合：共享权重 + 域增量（也可改为乘法，视实验而定）
            w = self.shared_kernels[i] + delta_w                                    # [B, Din, Dout]
            delta_b = self.domain_bias_embs[i](domain_index)                        # [B, Dout]
            b = self.shared_biases[i] + delta_b                                     # [B, Dout]

            # 线性层（按样本/域使用其专属参数）
            x = tf.expand_dims(x, axis=1)                                           # [B, 1, Din]
            x = tf.matmul(x, w) + tf.expand_dims(b, 1)                              # [B, 1, Dout]
            x = tf.squeeze(x, axis=1)                                               # [B, Dout]

            # 激活 + Dropout（保持轻量）
            x = self.activation(x)
            x = self.dropout(x, training=training)
        return x

Partitioned Normalization

在神经网络训练时，为了加快模型的收敛常会在模型中加入BN(Batch Normalization)。但是在多场景建模中，样本只在相同的场景内才满足独立同分布，多个场景混合的样本得到的统计量会忽略了不同场景独有的分布差异。为此应该让多场景中不同的场景独享统计量，这就是PN(Partitioned Normalization)提出的主要动机。

在介绍PN之前，先简单回顾一下经典的BN的原理：

(3.5.6)\[\mathbf{z'} = \gamma \frac{\mathbf{z} - \mathbf{E}}{\sqrt{\mathrm{Var} + \epsilon}} + \beta\]

其中\(\mathbf{E},\mathrm{Var}\)分别是移动的均值和方差，\(\gamma,\beta\)是可学习的参数用来对数据进行缩放和平移。

PN相比BN来说，不仅可学习的缩放和平移参数包括场景共享和独占两部分的参数，统计的移动均值和方差也是在不同场景样本上得到的，具体表示如下：

(3.5.7)\[\mathbf{z'} = (\gamma * \gamma_p) \frac{\mathbf{z} - \mathbf{E_p}}{\sqrt{\mathrm{Var_p} + \epsilon}} + (\beta + \beta_p)\]

其中\(\gamma,\beta\)和\(\gamma_p,\beta_p\)分别表示场景共享和独占的参数，\(\mathbf{E_p},\mathrm{Var_p}\)表示在场景\(p\)的样本中统计得到的移动均值和方差。由于PN是基于Batch样本计算的，为了得到不同场景下更稳定的均值和方差，训练时的Batch Size可以调的稍微大一些。

Partitioned Normalization的具体实现如下：

class PartitionedNormalization(tf.keras.layers.Layer):
    """
    领域分区归一化（简化版）
    - 核心思想：按 domain 将 batch 切分，对每个子批次单独做 BN，
      再把结果写回原位置，避免跨域统计混淆。
    - 实现要点：掩码取出 -> 逐域 BN -> scatter 回填。
    """
    def __init__(self, num_domain, name=None, **kwargs):
        super(PartitionedNormalization, self).__init__(name=name)
        self.num_domain = num_domain
        # 每个域一个 BN（带缩放与中心化），更直观体现“分区归一化”
        self.bn_list = [
            tf.keras.layers.BatchNormalization(center=True, scale=True, name=f"bn_{i}")
            for i in range(num_domain)
        ]

    def _grid_indices(self, rows, dim):
        y = tf.range(dim)
        x_grid, y_grid = tf.meshgrid(rows, y)
        return tf.transpose(tf.stack([x_grid, y_grid], axis=-1), [1, 0, 2])

    def call(self, inputs, training=None):
        # x: [B, D]；domain_index: [B]
        x, domain_index = inputs
        domain_index = tf.cast(tf.reshape(domain_index, [-1]), tf.int32)
        dim = tf.shape(x)[-1]

        y = x
        for i, bn in enumerate(self.bn_list):
            mask = tf.equal(domain_index, i)
            def update():
                xi = tf.boolean_mask(x, mask)                    # 取该域样本
                yi = bn(xi, training=training)                   # 用该域统计做 BN
                rows = tf.boolean_mask(tf.range(tf.shape(x)[0]), mask)
                grid = self._grid_indices(rows, dim)             # 生成 (row, col) 坐标
                return tf.reshape(tf.tensor_scatter_nd_update(y, grid, yi), tf.shape(y))

            y = tf.cond(tf.reduce_any(mask), update, lambda: y)
        return y

辅助网络

为了进一步加强场景特征对模型输出的影响，在STAR中还会单独构建一个场景的辅助网络(Auxiliary Network)，辅助网络将场景特征和其他特征共同输入到浅层网络中得到一个辅助的Logits，最终和主网络的Logits相加计算得到最终的CTR预估值：

(3.5.8)\[pCTR = Sigmoid(Logits_{main} + Logits_{aux})\]

STAR模型的实现代码如下：

# 核心思路：主干 Star FCN + 辅助 DNN，两者按域归一化后融合
# 1) 输入层：构建所有特征的输入，并取出域特征（用于分域）
input_layer_dict = build_input_layer(feature_columns)
domain_input = input_layer_dict[domain_feature_name]

# 2) 获取 dnn 组与 domain 组的表示
dnn_inputs = concat_group_embedding(group_embedding_feature_dict, 'dnn')          # [B, dnn_dim]
domain_embeddings = concat_group_embedding(group_embedding_feature_dict, 'domain') # [B, domain_dim]

# 3) 主干分支（Star FCN）：对 dnn
fcn_inputs = PartitionedNormalization(num_domain=num_domains, name="fcn_pn_layer")(
    [dnn_inputs, domain_input]
)
fcn_output = StarTopologyFCN(num_domains, star_dnn_units, star_fcn_activation,
                                dropout, l2_reg, name="star_fcn_layer")([fcn_inputs, domain_input])
fcn_logit = PredictLayer(activation=None, name='fcn_logits')(fcn_output)

# 4) 辅助分支（Aux DNN）：将域嵌入与 dnn 输入拼接，进行轻量 DNN
aux_inputs = concat_func([domain_embeddings, dnn_inputs], axis=-1)                 # [B, domain_dim + dnn_dim]
aux_inputs = PartitionedNormalization(num_domain=num_domains, name="aux_pn_layer")(
    [aux_inputs, domain_input]
)
aux_output = DNNs(aux_dnn_units, dropout_rate=dropout)(aux_inputs)
aux_logit = PredictLayer(activation=None, name='aux_logits')(aux_output)

# 5) 融合：主干与辅助分支的 logit 相加，得到最终的表征
final_logits = add_tensor_func([fcn_logit, aux_logit])

final_prediction = PredictLayer(activation=None, name='final_prediction')(final_logits)

代码实践

run_experiment('star')

+--------+--------+------------+
|    auc |   gauc |   val_user |
+========+========+============+
| 0.6648 | 0.6244 |        693 |
+--------+--------+------------+