4.2. 基于个性化的重排¶

上一节我们探讨了基于贪心策略的重排序方法，如MMR (Maximal Marginal Relevance) 和 DPP (Determinantal Point Processes)。这些方法通过显式定义多样性、相关性或覆盖度的优化目标，在初始排序列表上进行局部调整。它们计算高效且可解释性强，但在处理复杂的物品间相互影响和深度个性化方面存在局限：目标函数往往需要手工设计，难以捕捉高阶、非线性的交互模式；同时，将用户个性化信息深度融入列表级优化也颇具挑战。

接下来会介绍两个经典的个性化重排模型：PRM和PRS。

4.2.1. PRM¶

PRM (Personalized Re-Ranking Model) (Pei et al., 2019) 的提出，标志着重排序技术从基于规则/启发式向数据驱动、端到端学习的重要转变。其核心思想是：利用强大的序列建模能力（Transformer）自动学习列表中物品间复杂的相互影响，并将细粒度的用户个性化信息深度融入整个重排序过程，通过最大化列表级效用目标（如点击率）进行全局优化。 PRM不再依赖预设的多样性公式，而是让模型直接从数据中学习最优的物品组合方式，同时精准反映用户的独特偏好。下图展示了PRM的整体架构：

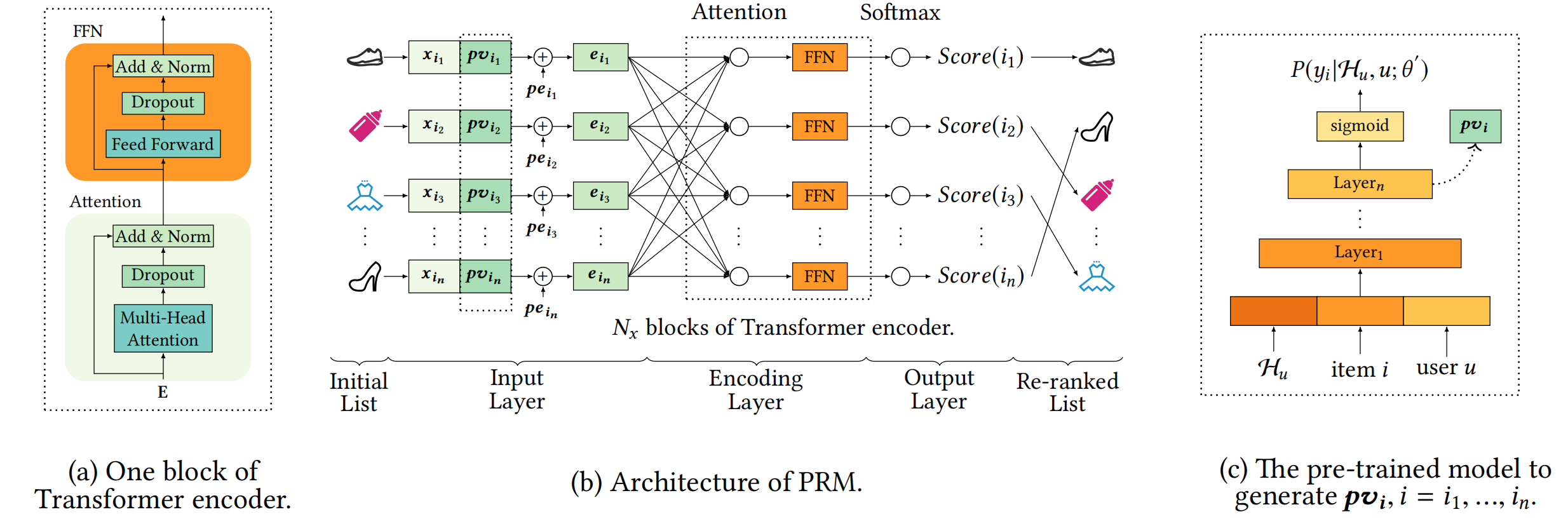
../_images/prm_architecture.png — 图4.2.1 PRM模型架构¶

输入层

输入层的核心任务是为初始列表 \(S = [i_1, i_2, ..., i_n]\) 中的每个物品 \(i_j\) 准备一个信息丰富且适合后续处理的初始表示。这个表示需要包含两个至关重要的方面：

物品自身特征 (\(X\))：例如物品ID嵌入、类别、标签、统计特征等基础信息。
用户对该物品的个性化偏好 (\(PV\))：这是PRM实现“个性化”重排序的灵魂所在！它编码了用户\(u\)与物品\(i_j\)之间独特的互动关系和偏好程度。PV 的生成是其关键创新点，我们将在后面详细探讨。

PRM采用了一个直观且有效的方法：将物品的原始特征向量 \(x_j\) 与其对应的个性化向量 \(pv_j\) 拼接（Concatenate）起来，形成一个更全面的基础表示 \([x_j; pv_j]\)。

然而，仅有个性化和物品特征还不够。基础排序模型给出的初始列表 \(S = [i_1, i_2, ..., i_n]\) 本身包含潜在的序列信息（例如，排名靠前的物品可能相关性更高）。为了利用这一信息，PRM引入了标准的位置嵌入 (Positional Embedding, PE)。这就像给列表中的每个位置（第1位、第2位…第n位）赋予一个独特的、可学习的向量标识。最终，每个物品进入编码层之前的输入表示\(E\)是其融合特征与位置信息的叠加：

(4.2.1)¶\[E = [\text{物品自身特征}(x_j) ; \text{个性化向量}(pv_j)] + \text{位置嵌入}(pe_j)\]

这个组合结果通常会经过一个简单的前馈网络（线性变换）进行维度调整，以适应后续Transformer编码器的输入要求。

编码层

输入层提供了带有个性化烙印和位置信息的物品序列。编码层的核心使命是利用 Transformer 架构的强大序列建模能力，让列表中的所有物品能够充分“沟通”和“互动”，从而捕捉它们之间复杂的、高阶的相互影响。这对于重排序至关重要，因为：

用户是否点击列表中的第 j 个物品，很可能受到第 k 个（甚至更远）物品的显著影响（例如，它们是替代品、互补品，或者提供了多样性）。
这种影响往往是长距离的，不受物品在列表中初始物理位置的限制。

Transformer的核心武器是自注意力机制 (Self-Attention)。它赋予了序列中每个物品一项能力：可以动态地“关注”序列中的所有其他物品（包括它自己）。其工作原理是计算每个物品的查询向量(Query)与其他物品的键向量(Key)的相似度，得到一个注意力权重。这个权重决定了在更新当前物品表示时，应该聚合(Value) 多少来自其他物品的信息。公式 \(Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d}}) V\)精炼地描述了这个加权聚合过程。

为了更全面、更鲁棒地捕捉列表中物品间复杂的相互影响，PRM采用了多头注意力，这些多头注意力模块被组织在标准的 Transformer 编码器块(Block) 中，每个块包含一个多头自注意力层和一个前馈神经网络层。PRM通过堆叠多层，使模型能够在初始交互表示的基础上，逐层提炼更复杂、更高阶的物品间依赖关系。最终，编码层输出每个物品的高级表示\(F^{N_x}\)，它深度融合了物品自身特征、用户个性化偏好以及在整个列表上下文感知到的深度交互信息。

输出层

PRM采用了一个轻量级但有效的输出结构：对每个物品的高级表示 \(F^{N_x}\) 应用一个线性变换（\(W^f \cdot F^{N_x} + b^f\)），将其映射为一个标量分数（或称 logit）。这个分数初步反映了该物品在重排序后的列表中的相对价值。将列表中所有物品的标量分数输入一个 Softmax 函数。Softmax 在此扮演两个关键角色：

归一化：将所有分数转换为一个概率分布 \(P(y_i | X, PV; \hat{\theta})\)，其中 \(y_i\) 表示物品 \(i\) 在最终列表中被认为是最合适（或最可能被点击）的概率。所有物品的概率之和为1。
隐含相对关系建模： Softmax 函数的特性使得每个物品的最终概率不仅取决于它自身的分数，也取决于它与列表中所有其他物品分数的相对比较。这天然地符合重排序需要评估物品间相对重要性的需求

个性化向量 (PV) 的生成

回顾整个流程，个性化向量 \(PV\) 是PRM区别于普通重排序模型、实现真正“个性化”的关键所在。那么，\(PV\) 从何而来？PRM采用了一个巧妙且实用的策略：利用预训练的点击率预估模型来生成PV。

预训练模型的作用：这个模型在海量的用户历史行为数据（用户ID、物品ID、上下文特征、历史点击/转化日志）上进行训练。它的核心任务是学习预测：给定用户 \(u\) 及其行为历史 \(H_u\)，用户点击某个候选物品 \(i\) 的概率 \(P(y_i | H_u, u; \theta')\)。
提取个性化向量： PRM 并不直接使用预训练模型预测的点击概率本身。相反，它提取该模型在输出最终点击概率（通常经过Sigmoid激活）之前的那个隐藏层的激活值。这个隐藏层的向量，蕴含了预训练模型学习到的、关于“用户 \(u\) 对物品 \(i\) 偏好程度”的丰富、抽象的信息，将其作为物品 \(i\) 相对于用户 \(u\) 的个性化向量 \(pv_i\)。
输入PRM：对于初始列表 \(S = [i_1, i_2, ..., i_n]\) 中的每个物品 \(i_j\)，都通过上述预训练模型计算出其对应的 \(pv_j\)，然后作为关键输入送入PRM的输入层。

PRM核心代码如下：

def build_prm_model(feature_columns,
                    max_seq_len=30,
                    transformer_blocks=2,
                    nums_head=1,
                    dropout_rate=0.1,
                    intermediate_dim=64,
                    pos_emb_trainable=True,
                  ):
    input_layer_dict = build_input_layer(feature_columns)
    group_embedding_feature_dict = build_group_feature_embedding_table_dict(feature_columns, input_layer_dict, prefix="embedding/")
    user_part_embedding = concat_group_embedding(group_embedding_feature_dict, 'user_part') # BxD
    # 复制成序列长度份数
    user_part_embedding = tf.keras.layers.Lambda(lambda x: tf.tile(tf.expand_dims(x, axis=1),
        [1, max_seq_len, 1]))(user_part_embedding) # [None, max_len, dim]

    item_part_embedding = concat_group_embedding(group_embedding_feature_dict, 'item_part', axis=-1, flatten=False) # Bxmax_seq_lenxK
    pv_embeddings = input_layer_dict['pv_emb'] # Bxmax_seq_lenxD
    item_embeddings = input_layer_dict['item_emb'] # Bxmax_seq_lenxD

    page_embedding = concat_func([user_part_embedding, item_part_embedding, pv_embeddings, item_embeddings], axis=-1) # [None, max_len, dim]

    position_embedding = PositionEncodingLayer(
        dims=feature_columns[0].emb_dim,
        max_len=max_seq_len,
        trainable=pos_emb_trainable,
        initializer='glorot_uniform')(page_embedding)

    enc_inputs = add_func([page_embedding, position_embedding])

    for _ in range(transformer_blocks):
        enc_inputs = TransformerEncoder(
                                        intermediate_dim,
                                        nums_head,
                                        dropout_rate,
                                        activation="relu",
                                        normalize_first=True,
                                        is_residual=True
                                    )(enc_inputs)

    enc_output = tf.keras.layers.Dense(intermediate_dim, activation='tanh')(enc_inputs)
    enc_output = tf.keras.layers.Dense(1)(enc_output)
    flat = tf.keras.layers.Flatten()(enc_output)
    score_output = tf.keras.layers.Activation(activation='softmax')(flat)

    # 构建模型
    model = tf.keras.Model(inputs=list(input_layer_dict.values()), outputs=score_output)
    return model

代码实践

import sys
import funrec
from funrec.utils import build_metrics_table

config = funrec.load_config('prm')
train_data, test_data = funrec.load_data(config.data)
feature_columns, processed_data = funrec.prepare_features(config.features, train_data, test_data)
model = funrec.train_model(config.training, feature_columns, processed_data)
metrics = funrec.evaluate_model(model, processed_data, config.evaluation, feature_columns)
print(build_metrics_table(metrics))

+----------+---------+--------------+-------------+------------+-----------+--------------+-------------+------------+-----------+--------+-------+
|   map@10 |   map@5 |   new_map@10 |   new_map@5 |   new_p@10 |   new_p@5 |   old_map@10 |   old_map@5 |   old_p@10 |   old_p@5 |   p@10 |   p@5 |
+==========+=========+==============+=============+============+===========+==============+=============+============+===========+========+=======+
|   0.2504 |  0.2456 |       0.2504 |      0.2456 |     0.0706 |     0.087 |       0.2954 |      0.2824 |     0.0936 |    0.1196 | 0.0706 | 0.087 |
+----------+---------+--------------+-------------+------------+-----------+--------------+-------------+------------+-----------+--------+-------+

4.2.2. PRS¶

虽然PRM通过Transformer架构实现了端到端的个性化重排序，但它仍然存在一个根本性的局限：缺乏对排列组合影响的深度理解。想象这样一个场景：用户面对商品列表 [A, B, C] 时毫无购买欲望，但当看到 [B, A, C] 这个排列时却购买了商品A。这种现象被称为 排列变异影响 (Permutation-Variant Influence)。一个可能的解释是：将价格较高的商品B放在前面，会让用户觉得商品A相对便宜，从而激发购买欲望。

../_images/prs_permutation_influence.png — 图4.2.2 排列变异影响¶

这个观察引出了一个重要问题：传统的重排序方法（包括PRM）主要关注单个物品的分数优化，却忽略了物品排列顺序本身对用户行为的影响。

PRS (Feng et al., 2021) 的设计哲学可以用一个简单而深刻的题目来概括：如果我们能够评估所有可能的物品排列组合，并选择其中用户体验最佳的那一个，会怎样？ 当然，对于包含n个物品的列表，所有可能的排列数量是n!，这在计算上是不可行的。PRS的巧妙之处在于提出了一个两阶段的解决方案：

PMatch阶段：通过智能搜索算法快速筛选出少数几个“有希望”的候选排列
PRank阶段：使用专门的神经网络模型精确评估这些候选排列的质量，选出最优解

这种设计既保证了计算效率，又能够捕捉到排列组合对用户体验的深层影响。

PRS整体架构

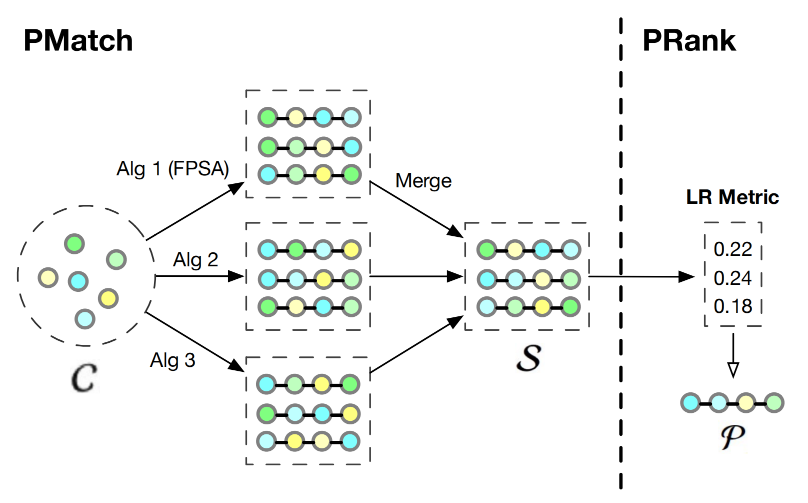
../_images/prs_framework.png — 图4.2.3 PRS框架整体架构¶

4.2.2.1. PMatch阶段：智能候选排列生成¶

PMatch (Permutation-Matching) 阶段的使命是从指数级的排列空间中，高效地识别出最有潜力的候选排列。这个阶段采用了一种名为FPSA (Fast Permutation Searching Algorithm) 的创新算法，它结合了目标导向的beam search和两个关键的用户行为预测模型。

离线训练：双模型预测体系

PMatch阶段需要两个point-wise预测模型的支持：

CTR模型：预测用户点击某个物品的概率 \(P_{CTR}(i|u)\)
Next模型：预测用户在浏览完当前物品后继续浏览下一个物品的概率 \(P_{Next}(i|u)\)

Next模型的引入是PRS的一个重要创新。它反映了这样一个现实：用户的浏览行为具有连续性，某个物品不仅要能吸引用户点击，还要能够“引导”用户继续探索列表中的后续内容。这两个模型都采用标准的point-wise建模方式：

(4.2.2)¶\[f_{CTR}(x_u, x_i) = \sigma(W_{CTR} \cdot [x_u; x_i] + b_{CTR})\]

(4.2.3)¶\[f_{Next}(x_u, x_i) = \sigma(W_{Next} \cdot [x_u; x_i] + b_{Next})\]

其中 \(x_u\) 和 \(x_i\) 分别表示用户和物品的特征向量，\(\sigma\) 是sigmoid激活函数。两个模型都使用交叉熵损失进行训练。

在线服务：FPSA算法

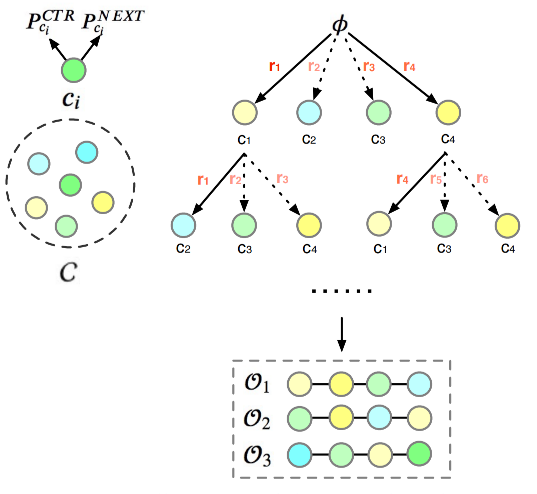
../_images/prs_fpsa.png — 图4.2.4 FPSA结构图¶

上图展示了FPSA算法在整个PRS框架中的位置和核心组件。我们可以看到：

输入处理：算法接收来自ranking阶段的候选物品集合C，每个物品都有丰富的特征表示
双模型预测体系：
- CTR模型：预测每个物品的点击概率 \(P^{CTR}_i\)
- Next模型：预测用户浏览完物品i后继续浏览的概率 \(P^{NEXT}_i\)
Beam Search核心：通过树状搜索逐步构建候选排列，每一步都基于奖励函数进行剪枝
奖励计算机制：融合rPV和rIPV两个指标，平衡浏览深度和点击收益

FPSA算法的核心创新在于将用户的浏览行为建模为一个序列决策过程。传统的重排序方法往往独立地评估每个物品，而FPSA认识到：物品在序列中的价值不仅取决于自身特征，更取决于它在整个浏览路径中的作用。

算法定义了两个关键的奖励指标：

rPV (Page View Reward)：衡量排列能够带来的总浏览深度，鼓励选择那些能引导用户深度浏览的物品组合
rIPV (Item Page View Reward)：衡量排列中物品被点击的总概率，确保排列具有足够的商业价值

FPSA算法流程如下

FPSA核心代码如下：

def fpsa_algorithm(items, ctr_scores, next_scores, beam_size=5, max_length=10, alpha=0.5, beta=0.5):
    """
    Fast Permutation Searching Algorithm (根据Algorithm 1实现)

    Args:
        items: 候选物品列表 (对应Algorithm 1的Input ranking list C)
        ctr_scores: 每个物品的CTR分数字典 (对应P^CTR)
        next_scores: 每个物品的Next分数字典 (对应P^NEXT)
        beam_size: beam search的大小 (对应Beam size integer k)
        max_length: 输出序列的最大长度 (对应Output length n)
        alpha, beta: 融合系数 (对应Fusion coefficient float $\alpha, \beta$)

    Returns:
        候选排列集合 (对应Output: Candidate list set S)
    """
    S = [()]  # 候选列表集合，初始包含空序列
    R = {}    # 估计奖励集合

    for i in range(1, max_length + 1):
        St = S.copy()

        S = []
        R = {}

        for O in St:
            for ci in items:
                if ci not in O:
                    Ot = O + (ci,)

                    r = calculate_estimated_reward(Ot, ctr_scores, next_scores, alpha, beta)

                    R[Ot] = r
                    S.append(Ot)

        S = sorted(S, key=lambda x: R[x], reverse=True)[:beam_size]

    return S

def calculate_estimated_reward(O, ctr_scores, next_scores, alpha, beta):
    """
    计算估计奖励 (对应Algorithm 1的第19-28行 Calculate-Estimated-Reward函数)

    Args:
        O: 当前排列序列
        ctr_scores: CTR分数字典
        next_scores: Next分数字典
        alpha, beta: 融合系数

    Returns:
        估计奖励值
    """
    if not O:
        return 0.0

    r_pv = 1.0
    r_ipv = 0.0

    p_expose = 1.0

    for ci in O:
        p_ctr_ci = ctr_scores[ci]
        p_next_ci = next_scores[ci]

        r_ipv = r_ipv + p_expose * p_ctr_ci

        p_expose *= p_next_ci

    r_pv = p_expose

    r_sum = alpha * r_pv + beta * r_ipv

    return r_sum

# 使用示例保持不变
def get_ctr_score(item):
    """获取物品的CTR分数"""
    # 这里应该调用预训练的CTR模型
    pass

def get_next_score(item):
    """获取物品的Next分数"""
    # 这里应该调用预训练的Next模型
    pass

# 完整的FPSA调用
def run_fpsa(items, beam_size=5, max_length=10):
    # 预计算所有物品的CTR和Next分数
    ctr_scores = {item: get_ctr_score(item) for item in items}
    next_scores = {item: get_next_score(item) for item in items}

    # 运行FPSA算法
    candidates = fpsa_algorithm(
        items=items,
        ctr_scores=ctr_scores,
        next_scores=next_scores,
        beam_size=beam_size,
        max_length=max_length,
        alpha=0.5,  # 可调节的融合系数
        beta=0.5
    )

    return candidates

这个算法的精妙之处在于：

rPV 鼓励选择那些能够引导用户深度浏览的物品排列
rIPV 确保排列中的物品具有足够的吸引力
曝光概率的递减 真实地模拟了用户浏览行为：越往后的物品，被用户看到的概率越低

4.2.2.2. PRank阶段：深度排列评估¶

PRank (Permutation-Ranking) 阶段接收PMatch生成的候选排列，使用一个专门设计的神经网络模型DPWN (Deep Permutation-Wise Network) 来精确评估每个排列的质量。

DPWN模型架构

DPWN的设计理念是：排列中每个物品的价值不仅取决于它自身的特征，更取决于它在整个序列上下文中的位置和作用。为了捕捉这种复杂的序列依赖关系，DPWN采用了Bi-LSTM架构：

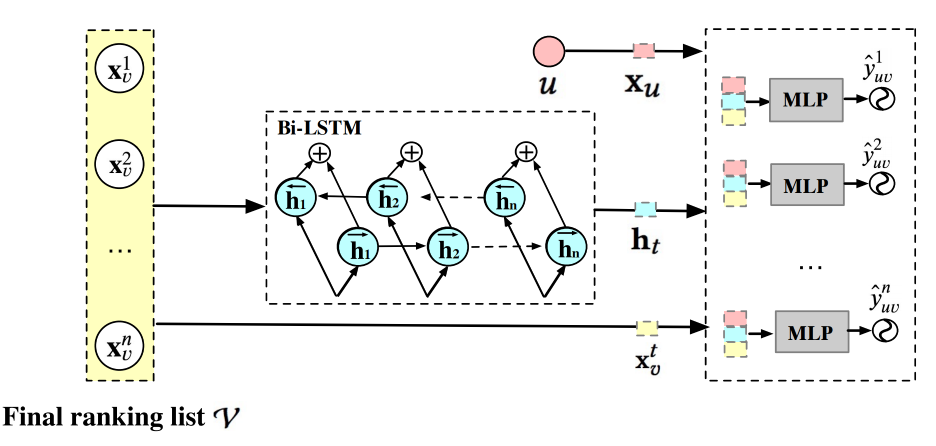
../_images/prs_dpwn_architecture.png — 图4.2.5 DPWN模型架构¶

模型结构介绍

序列编码层：对于输入序列中的第t个物品，DPWN使用双向LSTM计算其上下文表示：

(4.2.4)¶\[\overrightarrow{h_t} = LSTM_{forward}(x_{v_t}, \overrightarrow{h_{t-1}})\]

(4.2.5)¶\[\overleftarrow{h_t} = LSTM_{backward}(x_{v_t}, \overleftarrow{h_{t+1}})\]

(4.2.6)¶\[h_t = [\overrightarrow{h_t}; \overleftarrow{h_t}]\]

其中 \(x_{v_t}\) 是第t个物品的特征向量，\(h_t\) 是融合了前向和后向信息的隐状态。

特征融合层：将序列表示与用户特征和物品特征进行融合：

(4.2.7)¶\[z_t = [h_t; x_u; x_{v_t}]\]

其中 \(x_u\) 是用户特征向量。

预测层：通过多层感知机预测每个位置的点击概率：

(4.2.8)¶\[p_t = \sigma(MLP(z_t))\]

List Reward (LR) 计算

PRank阶段的核心评估指标是List Reward，它被定义为排列中所有物品预测点击概率的总和：

(4.2.9)¶\[LR(O) = \sum_{t=1}^{|O|} p_t\]

这个简单而有效的指标反映了整个排列的预期收益。在线服务时，PRank会计算每个候选排列的LR值，并选择LR最高的排列作为最终输出。