3.5.2. 动态权重建模¶
在前一小节,我们探讨了 HMoE 和 STAR 这类基于多塔结构的多场景建模方案。它们通过为不同场景构建独立的“专家”网络或塔底参数,有效地捕获了场景间的特异性信息,解决了模型在跨场景迁移时因参数冲突导致的性能下降问题。这类模型的核心思想是“分而治之”,通过物理隔离的参数空间来保障场景的独特性。
为了在保持模型参数高效共享的同时,实现更细粒度、更灵活的场景感知能力,研究者们提出了“动态权重建模”的新范式。 这类方法的核心理念不再是构建物理隔离的参数塔,而是让模型的核心网络参数在不同场景下共享一个基础,但通过动态生成的、与场景/样本高度相关的“权重”来调制(Modulate)这些共享参数的行为。这相当于为共享网络“注入”了场景和样本的上下文信息,使其能够根据当前上下文动态调整其计算逻辑。
本节将重点介绍几种具有代表性的动态权重建模方案,它们展示了如何巧妙地设计“权重生成器”来调制共享网络。它们通过引入动态性,在参数效率、灵活性和性能之间取得了更优的平衡,为构建更加智能、自适应的多场景推荐系统提供了有力工具。
3.5.2.1. PEPNET¶
PEPNet(Parameter and Embedding Personalized Network) (Chang et al., 2023) 核心目标是解决多场景多任务中的双重跷跷板效应(Double Seesaw Phenomenon)。
场景跷跷板(Domain Seesaw):混合训练时不同场景数据分布差异导致表征无法对齐;
任务跷跷板(Task Seesaw):多任务间稀疏性与依赖关系失衡导致目标相互抑制;
PEPNet通过两大模块实现动态权重调控,形成“底层场景适配 + 顶层任务适配”的分层个性化,这也是PEPNet实现参数个性化的核心思路,PEPNet模型结构如下:
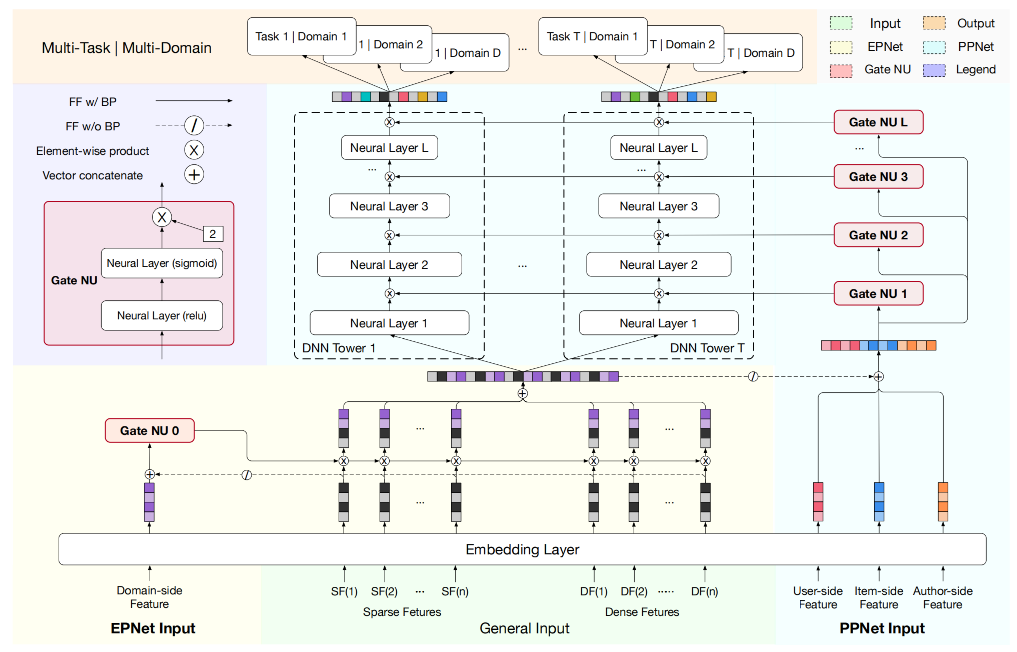
图3.5.5 PEPNet模型结构¶
在介绍PEPNet的量大核心组件之前,需要先简单介绍一个通过模块Gate NU,EPNet与PPNet均基于轻量级门控单元Gate NU构建,以极低参数量实现参数个性化,Gate NU受语音识别领域LHUC (Swietojanski et al., 2016) 模型启发,通过两层网络生成动态缩放权重:
其中\(\mathbf{x}\)为个性化先验特征(如场景ID或用户画像),\(\gamma\)为缩放强度(经验值设为2)。输出\(\boldsymbol{\delta}\)与目标参数维度对齐,通过逐元素相乘(\(\otimes\))实现调制。Gate NU的代码实现如下:
class GateNU(tf.keras.layers.Layer):
"""
两层门控网络(NU):用于为不同分支/专家动态生成权重或系数。
结构:Dense(ReLU) -> Dense(Sigmoid) -> gamma 缩放。
"""
def __init__(self,
hidden_units,
gamma=2.,
l2_reg=0.):
assert len(hidden_units) == 2
self.gamma = gamma
self.dense_layers = [
tf.keras.layers.Dense(hidden_units[0], activation="relu", kernel_regularizer=tf.keras.regularizers.l2(l2_reg)), # 第一层:非线性特征提取
tf.keras.layers.Dense(hidden_units[1], activation="sigmoid", kernel_regularizer=tf.keras.regularizers.l2(l2_reg)) # 第二层:输出 (0,1) 门值
]
super(GateNU, self).__init__()
def call(self, inputs):
output = self.dense_layers[0](inputs) # [B, hidden_units[0]]
# 乘以 gamma 对 Sigmoid 输出进行缩放。
output = self.gamma * self.dense_layers[1](output) # [B, hidden_units[1]]
return output
3.5.2.1.1. EPNet:场景感知的嵌入个性化¶
在实际的推荐模型中,特征Embedding层的参数量往往是最大的,共享底层Embedding也成为了业界标准的做法。但在多场景建模中,这种底层共享的机制更多的强调的是不同场景之间的共性,忽略了不同场景下Embedding的差异性。为此EPNet在Embedding层的基础上,将场景先验信息通过门控机制的方式以较低的参数量实现Embedding层的场景个性化。
EPNet 中Embedding层的门控单元\(U_{ep}\),以场景共享Embedding \(E\)和输入的场景先验特征的Embedding \(E(\mathcal{F}_d)\)拼接后的结果作为输入,EPNet的场景个性化输出\(\delta_{domain}\)表示如下:
其中,\(U_{ep}\)是EPNet模块的Gate NU网络。
为了让场景感知的个性化模块EPNet不影响底层共享Embedding的学习,在计算个性化门控结果时让共享Embedding层的梯度不反向传播,\(\oslash\)表示的是Stop Gredient。
然后,通过元素级乘积得到场景个性化的Embedding表征\(O_{ep}\):
通过将场景个性化先验信息整合到Embedding层中,EPNet可以有效地平衡多场景之间的共性和差异。
EPNet的实现代码如下:
class EPNet(tf.keras.layers.Layer):
def __init__(self,
l2_reg=0.,
**kwargs):
self.l2_reg = l2_reg
self.gate_nu = None
super(EPNet, self).__init__( **kwargs)
def build(self, input_shape):
assert len(input_shape) == 2
shape1, shape2 = input_shape
self.gate_nu = GateNU(hidden_units=[shape2[-1], shape2[-1]], l2_reg=self.l2_reg)
def call(self, inputs, *args, **kwargs):
domain, emb = inputs
# stop_gradient 阻断系数支路对 emb 的反向梯度,避免过度耦合。
return self.gate_nu(tf.concat([domain, tf.stop_gradient(emb)], axis=-1)) * emb # 输出形状 [B, D_emb]
3.5.2.1.2. PPNet:用户感知的参数个性化¶
EPNet解决的是多场景跷跷板问题,PPNet则更多考虑的是多任务之间的跷跷板。相比MMOE,PLE等其他多任务模型是任务级的个性化而言,PPNet则可以看成是样本粒度的个性化。PEPNet将用户ID、内容ID及作者ID作为个性化的先验特征,同时拼接上述EPNet得到的场景个性化的Embedding \(O_{ep}\)作为所有任务塔DNN参数个性化门控\(U_{pp}\)的输入。
为了防止PPNet模块影响到EPNet的参数更新,在计算\(\delta_{task}\)时\(O_{ep}\)部分不能梯度回传,\(\delta_{task}\)表示的是用户个性化门控的输出结果。
在得到了用户个性化的门控结果后,将其应用在所有任务塔中每个DNN网络上,从模型的结构图中可以看出不同任务塔中DNN的个性化门控是共享一份的,对于某个task的第\(l\)层DNN网络的参数个性化表达如下:
其中,\(L\)表示任务塔DNN网络的总层数,\(\mathbf{H}^{(l)}\)表示第\(l\)层DNN的输出同时也是第\(l+1\)层DNN的输入,\(\mathbf{O}^{(l)}_{pp}\)表示的是任务塔中第\(l\)层DNN的输出乘上个性化参数门控\(\delta_{task}\)后的输出结果。
PPNet实现代码如下:
class PPNet(tf.keras.layers.Layer):
# 核心:用 persona 生成逐层、逐塔的门控系数,对输出按维度缩放
def __init__(self,
multiples,
hidden_units,
activation,
dropout=0.,
l2_reg=0.,
**kwargs):
self.hidden_units = hidden_units
self.l2_reg = l2_reg
self.multiples = multiples
# 每个塔一份同结构的层
self.dense_layers = [
[tf.keras.layers.Dense(u, activation=activation,
kernel_regularizer=tf.keras.regularizers.l2(l2_reg))
for u in hidden_units]
for _ in range(multiples)
]
self.dropout_layers = [
[tf.keras.layers.Dropout(dropout) for _ in hidden_units]
for _ in range(multiples)
]
self.gate_nu = []
super(PPNet, self).__init__( **kwargs)
def build(self, input_shape):
# 为每层生成 gate:输出维度 units*multiples,后续按塔切片
self.gate_nu = [
GateNU([units * self.multiples, units * self.multiples], l2_reg=self.l2_reg)
for units in self.hidden_units
]
def call(self, inputs, training=None, **kwargs):
inputs, persona = inputs
# 先计算各层 gate(persona ⊕ stop_gradient(inputs))
gate_list = []
concat_in = tf.concat([persona, tf.stop_gradient(inputs)], axis=-1)
for i, gate in enumerate(self.gate_nu):
g = gate(concat_in) # [B, units*multiples]
g = tf.split(g, self.multiples, axis=1) # 每塔 [B, units]
gate_list.append(g)
# 按塔前向:逐层 Dense 后用 gate 做逐维调制
outputs = []
for n in range(self.multiples):
x = inputs
for i in range(len(self.hidden_units)):
x = gate_list[i][n] * self.dense_layers[n][i](x)
x = self.dropout_layers[n][i](x, training=training)
outputs.append(x)
return outputs
代码实践
from funrec import run_experiment
run_experiment('mmoe')
+----------------+---------------+-----------------+-------------+-----------------+----------------+------------------+--------------+---------------------+--------------------+----------------------+
| auc_is_click | auc_is_like | auc_long_view | auc_macro | gauc_is_click | gauc_is_like | gauc_long_view | gauc_macro | val_user_is_click | val_user_is_like | val_user_long_view |
+================+===============+=================+=============+=================+================+==================+==============+=====================+====================+======================+
| 0.6 | 0.425 | 0.4637 | 0.4962 | 0.5726 | 0.4467 | 0.4633 | 0.4942 | 928 | 530 | 925 |
+----------------+---------------+-----------------+-------------+-----------------+----------------+------------------+--------------+---------------------+--------------------+----------------------+
3.5.2.2. APG¶
在上一小节中,介绍了PEPNet通过场景/个性化的先验信号作为门控网络的输入,然后将门控网络的输出作用在底层Embedding和多目标塔的DNN层上,分别实现了基于门控的场景和多任务塔参数的个性化。本节将要介绍的APG (Adaptive Parameter Generation):cite:yan2022apg 模型同样希望实现样本粒度的个性化,但是做法却与PEPNet不太相同。APG 的核心思想是根据样本的不同动态生成相应的参数,从而提升模型的容量和表达能力。
APG通过样本感知的输入来生成自适应参数,这种方式可以应用在大多数的混合样本分布建模的问题中,多场景建模也不例外。具体来说,它提出了三种策略来生成样本的条件表示
Group-wise策略,适用于样本可以被分组成不同Group的情况,同一Group内的样本具有相似的模式,此时可以将Group相关特征作为输入
Mix-wise策略,将多种因素考虑进来生成,能够实现更细粒度的样本组划分,甚至可以做到 “千样本千模型”,如将<user, item> pair向量作为输入。
Self-wise策略,不需要先验知识的输入,直接将Deep CTR Models的隐层输出作为参数生成的输入。
在APG中通过MLP来自适应生成参数,将需要感知样本的输入\(\mathbf{z_i}\)输入到MLP中,然后Reshape成一个矩阵,
生成的参数矩阵,等价于MLP网络中的参数矩阵,通过矩阵乘法和激活函数实现和MLP一样的功能,如点击率模型的预估可以表示如下:
APG的核心思想比较简单,但要实际的上生产还需要经过一些优化。
低秩参数优化:借鉴低秩相关方法,APG假设自适应参数存在低秩关系,将参数矩阵分解成三个子矩阵相乘的形式。通过设置较小的秩值,可以有效控制计算和存储开销,同时在需要时也可以通过增大秩值来增加参数空间,参数分解表达式如下:
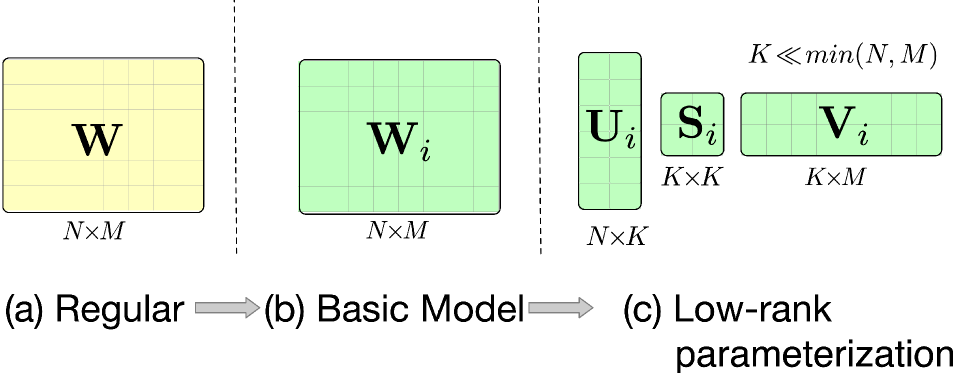
图3.5.6 参数分解¶
分解前向计算:在低秩参数化的基础上,APG设计了一种分解前向计算的方式,让输入依次乘以各个子矩阵。这种方式避免了计算开销较大的子矩阵乘操作,降低了整体的计算复杂度,
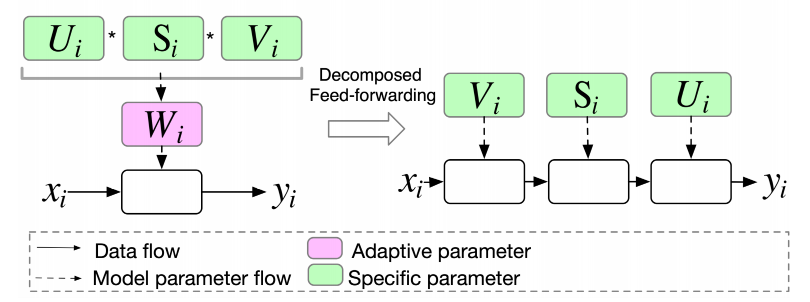
图3.5.7 前向计算优化¶
参数共享和过参数化:得益于矩阵分解带来的灵活性,APG将参数矩阵分为私有参数和共享参数两类。私有参数用于刻画不同样本的特性,共享参数则用于刻画样本共性。通过这种划分,APG在生成自适应参数的同时,也保留了对样本共性的表达,丰富了模型的表达能力。而且,由于私有参数规模的缩减,整体的计算和存储开销也得到了降低。此外,APG 将共享参数替代为两个大矩阵,这种设计不仅可以增加参数数量来提升模型容量,还具有隐含的正则效果,有助于防止过拟合。
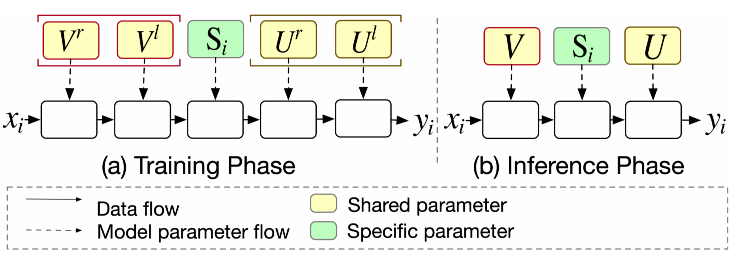
图3.5.8 参数共享及过参数化¶
APG Layer核心代码:
class APGLayer(tf.keras.layers.Layer):
"""
APG 自适应参数生成层(简化版)
核心:共享 U/V(输入→K、K→输出) + 样本私有 S_i(K×K)。
用场景/样本嵌入逐样本生成 S_i,对 K 表示进行调制,体现“按样本生成参数”的低秩形式。
仅保留 K 路:输入到 K(共享)→ K×K 调制(私有)→ K 到输出(共享)。
"""
def __init__(self, input_dim, output_dim, scene_emb_dim,
activation='relu', generate_activation=None,
inner_activation=None, mf_k=16,**kwargs):
super(APGLayer, self).__init__( **kwargs)
self.input_dim = input_dim
self.output_dim = output_dim
self.scene_emb_dim = scene_emb_dim
# 激活函数(可选)
self.activation = get_activation(activation) if activation else None
self.inner_activation = get_activation(inner_activation) if inner_activation else None
# 低秩维度 K:取输入/输出较小维度并缩减,强调“低秩”
min_dim = min(input_dim, output_dim)
self.k_dim = int(np.math.ceil(min_dim / mf_k)) # K ≪ min(N, M)
# 私有因子 S_i:从场景嵌入生成逐样本的 K×K 权重与 K 偏置
kk_weight_size = self.k_dim * self.k_dim # K×K
self.specific_weight_kk = DNNs([kk_weight_size], activation=generate_activation)
self.specific_bias_kk = DNNs([self.k_dim], activation=generate_activation)
# 共享因子 U/V:固定的 NK(输入→K)与 KM(K→输出)权重与偏置
self.shared_weight_nk = self.add_weight(shape=(input_dim, self.k_dim), initializer='glorot_uniform', name='shared_weight_nk')
self.shared_bias_nk = self.add_weight(shape=(self.k_dim,), initializer='zeros', name='shared_bias_nk')
self.shared_weight_km = self.add_weight(shape=(self.k_dim, output_dim), initializer='glorot_uniform', name='shared_weight_km')
self.shared_bias_km = self.add_weight(shape=(output_dim,), initializer='zeros', name='shared_bias_km')
def call(self, inputs):
"""
前向(分解前向):
x → NK(共享U)→ K → S_i(样本私有KK调制)→ K_mod → KM(共享V)→ 输出 → activation
"""
x, scene_emb = inputs
# 生成样本私有 KK 权重/偏置(S_i)
specific_weight_kk = self.specific_weight_kk(scene_emb) # [B, K*K]
specific_weight_kk = tf.reshape(specific_weight_kk, (-1, self.k_dim, self.k_dim)) # [B, K, K]
specific_bias_kk = self.specific_bias_kk(scene_emb) # [B, K]
# NK:输入到 K(共享 U)
k = tf.matmul(x, self.shared_weight_nk) + self.shared_bias_nk # [B, K]
if self.inner_activation:
k = self.inner_activation(k)
# KK:样本私有调制(批量矩阵乘):[B,1,K] × [B,K,K] → [B,1,K]
k_mod = tf.matmul(tf.expand_dims(k, 1), specific_weight_kk) # [B, 1, K]
k_mod = tf.squeeze(k_mod, 1) + specific_bias_kk # [B, K]
if self.inner_activation:
k_mod = self.inner_activation(k_mod)
# KM:K 到输出(共享 V)
output = tf.matmul(k_mod, self.shared_weight_km) + self.shared_bias_km
# 最终激活(可选)
if self.activation:
output = self.activation(output)
return output
代码实践
run_experiment('apg')
+--------+--------+------------+
| auc | gauc | val_user |
+========+========+============+
| 0.6777 | 0.6362 | 217 |
+--------+--------+------------+
3.5.2.3. M2M¶
在推荐系统的多场景建模中,动态参数生成技术展现出了巨大的潜力。除了 APG 模型外,基于元学习的多场景多任务商家建模(M2M) (Zhang et al., 2022) 是另一个在该领域具有重要影响的模型。M2M模型结构中主要包含底层的主干网络和顶层的元学习网络,下面将分别展开详细的介绍。
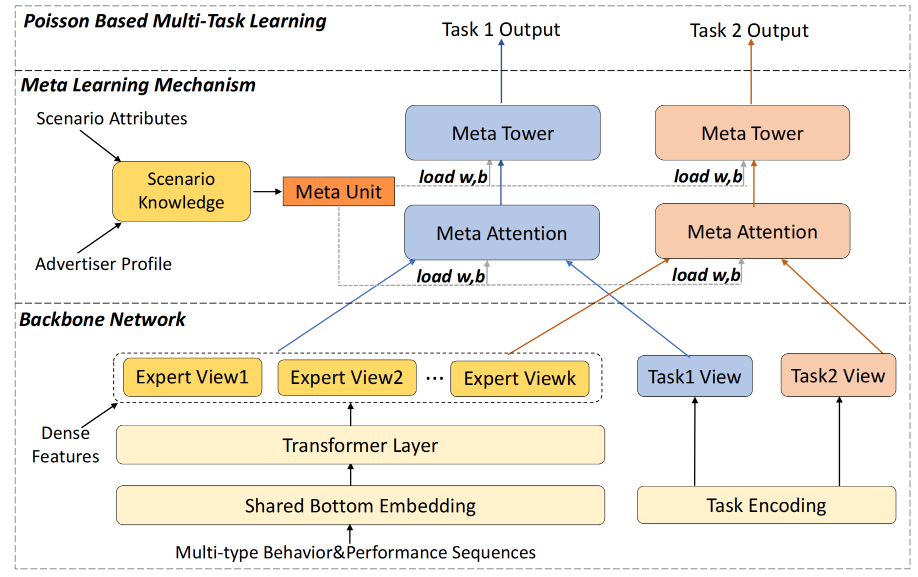
图3.5.9 M2M模型结构¶
3.5.2.3.1. 主干网络¶
主干网络中包括三部分内容:专家信息表征\(E_i\),任务信息表征\(T_t\),场景信息表征\(\tilde{\mathbf{S}}\)
专家信息表征:主干网络中有一个多专家的网络结构,每个专家输入的特征是将序列特征和其他特征拼接后的结果,而序列特征都由多头注意力机制进行聚合,第\(i\)个专家的数学表示为:
其中,\(X_{seq},X_{other}\)分别表示序列特征和除序列特征以外的其他特征,其中序列特征使用多头注意力网络进行聚合,其他特征Embedding直接进行拼接。\(f_{MLP}\)表示MLP网络,\(MAH\)表示多头注意力网络。
任务信息表征: 为了更好的表达不同任务的差异性,M2M将不同类别的任务进行全局表征,也就是对于每一条样本都会有对应多个任务表征特征。第t个任务对应的特征表征的数学形式:
场景信息表征:与任务信息表征类似,为了更好的表达场景之间的差异性,通过MLP网络对场景信息进行单独的表征,其输入的信息不仅包括了直接与场景相关的特征\(S\)还有跟广告主相关的特征\(A\),场景信息表征\(\tilde{\mathbf{S}}\)的数学形式为:
与任务信息表征不同的是,每条样本都有所属的场景,所以场景表达并不是全局的,此外由于该方法最早提出来是为了解决广告业务的,在实际的应用场景中,我们也可以将广告主相关的特征替换成我们业务中更合适的特征。
3.5.2.3.2. 元学习网络¶
在传统的机器学习中,权重\((W, b)\)通过反向传播在固定数据集上优化,学习目标是任务本身的表示。在M2M模型的元学习网络中,用一个MLP(元学习器)根据输入特征动态生成另一个网络(任务模型)的权重\((W, b)\)。这相当于让MLP学会“如何针对不同输入特征生成合适的任务模型参数”,而非直接学习任务本身,使任务模型动态适应不同任务/输入分布,这正是元学习的核心目标。
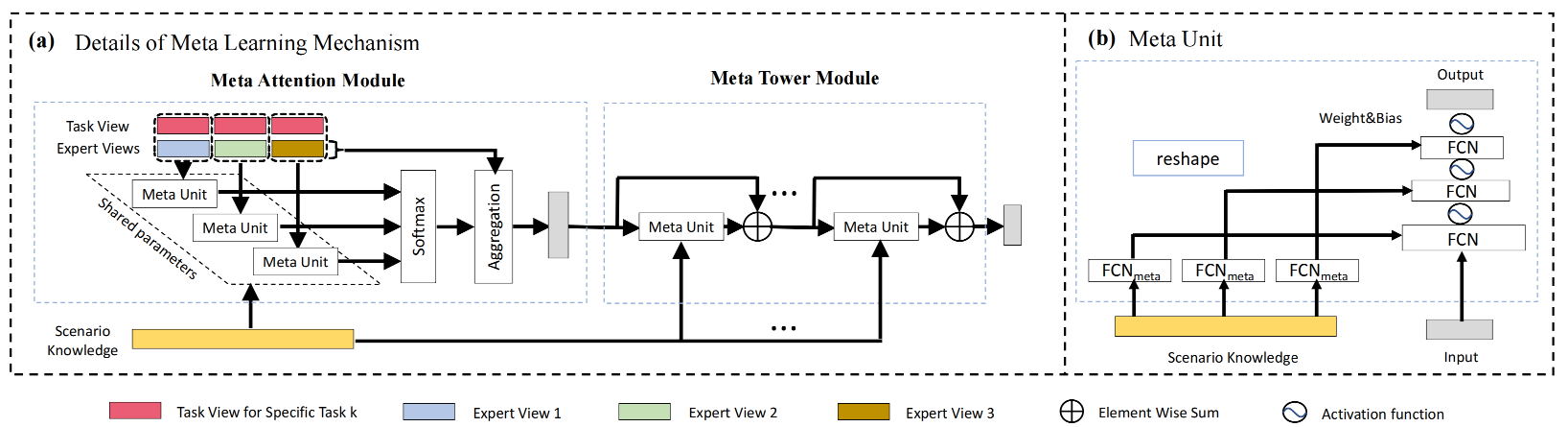
图3.5.10 Meta Unit网络结构¶
元学习单元原理 在M2M中元学习单元用来显式建模场景信息,为了更好的捕捉动态的场景相关信息,元学习单元将上述主干网络中得到的场景信息表征\(\tilde{\mathbf{S}}\)作为元学习单元的输入,元学习单元通过通过MLP网络将\(\tilde{\mathbf{S}}\)转换成每个场景动态的网络参数\((W,b)\),然后再将生成的参数作用于输入的特征上,下面\(Meta\)函数中包含了完整的元学习处理过程。
其中,元学习单元处理的过程如下:
元学习单元在后续多专家融合、多任务塔的建模中都有使用,为了方便理解,我们可以将经过元学习单元处理过的特征看成是,特征处理时注入了场景信息的一种类似MLP的通用结构。
Attention元网络
传统的多专家融合方式是将样本中的部分特征输入到门控网络中得到多个专家的融合参数,这种方式在模型训练的过程中,门控网络可以学习到任务与专家之间的关系,却忽略了场景的因素。为此,Attention网络在计算融合权重时引入场景信息,实现了不同场景的融合参数是更个性化的,权重系数的计算如下:
其中,\(\mathbf{R}_t\)是任务\(t\)融合多专家后的表征,\(E_i,T_t\)分别是第\(i\)个专家的特征和任务\(t\)的任务信息表征。
Tower元网络 为了进一步增强场景信息的表征能力,和Attention元网络类似,在多任务塔输出时也引入了元学习单元,并且通过残差的方式实现,Tower元网络的数学形式如下:
代码实践
run_experiment('m2m')
+----------------+---------------+-----------------+-------------+-----------------+----------------+------------------+--------------+---------------------+--------------------+----------------------+
| auc_is_click | auc_is_like | auc_long_view | auc_macro | gauc_is_click | gauc_is_like | gauc_long_view | gauc_macro | val_user_is_click | val_user_is_like | val_user_long_view |
+================+===============+=================+=============+=================+================+==================+==============+=====================+====================+======================+
| 0.6434 | 0.6459 | 0.6569 | 0.6487 | 0.591 | 0.6484 | 0.6176 | 0.619 | 217 | 131 | 217 |
+----------------+---------------+-----------------+-------------+-----------------+----------------+------------------+--------------+---------------------+--------------------+----------------------+
