3.2.1. 二阶特征交叉¶
Wide & Deep 模型虽然不错,但手工设计特征交叉实在太麻烦了。能不能让机器自己学会特征之间的关系呢?这就是我们要解决的问题。最直接的想法是让模型自动捕捉所有特征对之间的交互关系。但这里有个大问题:推荐系统的特征动辄成千上万,如果每两个特征都要学一个参数,参数量会爆炸。而且推荐数据本身就很稀疏,大部分特征组合根本没有足够的样本来训练。
所以关键是要找到一种巧妙的方法,既能自动学习特征交叉,又不会让参数太多。解决了这个问题后,还得考虑怎么把这些学到的交叉特征和深度网络结合起来。
3.2.1.1. FM: 从召回到精排的华丽转身¶
还记得我们在召回章节 2.3.1节 遇到的FM吗?当时我们看到它如何巧妙地将用户和物品分解成向量,通过内积实现高效的双塔召回。现在到了精排阶段,FM又要展现它的另一面了。
在召回时,FM主要解决的是“如何快速从海量物品中找到候选集”的问题。但在精排阶段,我们面临的挑战完全不同:如何自动学习特征之间的交叉关系,而不用手工一个个去设计。
这时候FM的核心思想就派上用场了——给每个特征学一个向量表示,然后用向量内积来捕捉特征间的关系。听起来很简单对吧?但这个简单的想法解决了一个大问题:不管你有多少特征,不管特征组合有多复杂,都能用同一套方法来处理。最关键的是,参数数量不会爆炸式增长,这对于推荐系统这种特征超多的场景来说太重要了。
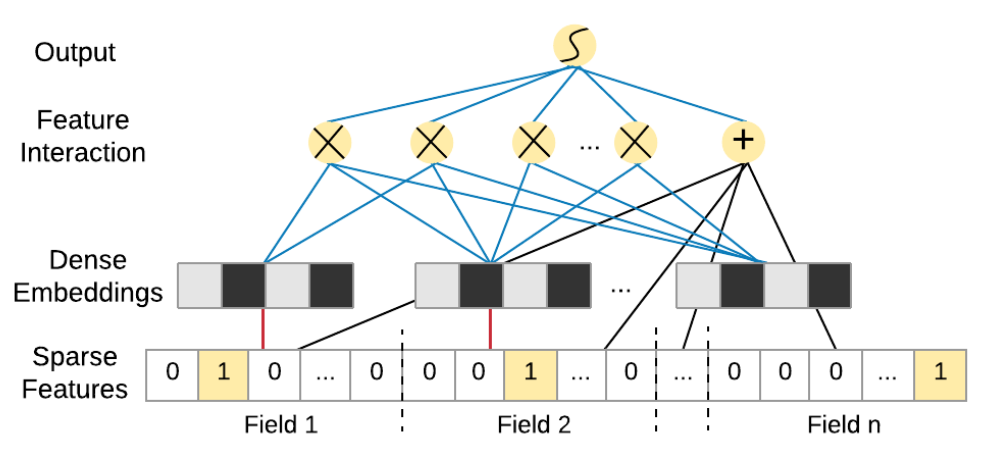
图3.2.1 FM模型结构¶
为了捕捉特征间的交互关系,一个直接的想法是在线性模型的基础上增加所有特征的二阶组合项,即多项式模型:
其中,\(w_0\) 是全局偏置项,\(w_i\) 是特征 \(x_i\) 的权重,\(w_{ij}\) 是特征 \(x_i\) 和 \(x_j\) 交互的权重,\(n\) 是特征数量。这个模型存在两个致命缺陷:第一,参数数量会达到 \(O(n^2)\) 的级别,在特征数量庞大的推荐场景下难以承受;第二,在数据高度稀疏的环境中,绝大多数的交叉特征 \(x_i x_j\) 因为在训练集中从未共同出现过,导致其对应的权重 \(w_{ij}\) 无法得到有效学习。
FM 模型巧妙地解决了这个问题。它将交互权重 \(w_{ij}\) 分解为两个低维隐向量的内积,即 \(w_{ij}=\langle\mathbf{v}_i,\mathbf{v}_j\rangle\)。这样,模型的预测公式就演变为:
其中\(\mathbf{v}_i,\mathbf{v}_j\) 分别是特征 \(i\) 和特征 \(j\) 的 \(k\) 维隐向量(Embedding)。\(k\) 是一个远小于特征数量 \(n\) 的超参数,\(\langle \mathbf{v}_i,\mathbf{v}_j \rangle\) 表示两个隐向量的内积,计算方式为 \(\sum_{f=1}^k v_{i,f} \cdot v_{j,f}\)。
这种参数共享的设计是 FM 的精髓所在。原本需要学习 \(O(n^2)\) 个独立的交叉权重 \(w_{ij}\),现在只需要为每个特征学习一个 \(k\) 维的隐向量 \(v_i\),总参数量就从 \(O(n^2)\) 降低到了 \(O(nk)\)。更重要的是,它极大地缓解了数据稀疏问题。即使特征 \(i\) 和 \(j\) 在训练样本中从未同时出现过,模型依然可以通过它们各自与其他特征(如 \(k\))的共现数据,分别学到有效的隐向量 \(v_i\) 和 \(v_j\)。只要隐向量学习得足够好,模型就能够泛化并预测 \(x_i\) 和 \(x_j\) 的交叉效果。此外,通过巧妙的数学变换,FM 的二阶交叉项计算复杂度可以从 \(O(kn^2)\) 优化到线性的 \(O(kn)\),(2.3.3) 使其在工业界得到了广泛应用。
核心代码
FM的核心在于将 \(O(n^2)\) 的二阶交叉项优化为线性复杂度。通过简单的代数变换,我们可以高效计算所有特征对的交互:
# FM层的核心计算:0.5 * ((sum(v))^2 - sum(v^2))
# inputs: [batch_size, field_num, embedding_size]
# 先求和再平方:(∑v_i)^2
square_of_sum = tf.square(
tf.reduce_sum(inputs, axis=1, keepdims=True)
) # [B, 1, D]
# 先平方再求和:∑(v_i^2)
sum_of_square = tf.reduce_sum(
inputs * inputs, axis=1, keepdims=True
) # [B, 1, D]
# FM二阶交互项
cross_term = 0.5 * tf.reduce_sum(
square_of_sum - sum_of_square, axis=2
) # [B, 1]
这个实现的巧妙之处在于,无论有多少特征,计算复杂度始终保持线性,使得FM能够处理推荐系统中常见的高维稀疏特征。
3.2.1.2. AFM: 注意力加权的交叉特征¶
FM 对所有特征交叉给予了相同的权重,但实际上不同交叉组合的重要性是不同的。AFM (Xiao et al., 2017) 在此基础上引入注意力机制,为不同的特征交叉分配权重,使模型能关注到更重要的交互。例如,在预测一位用户是否会点击一条体育新闻时,“用户年龄=18-24岁”与“新闻类别=体育”的交叉,其重要性显然要高于“用户年龄=18-24岁”与“新闻发布时间=周三”的交叉。
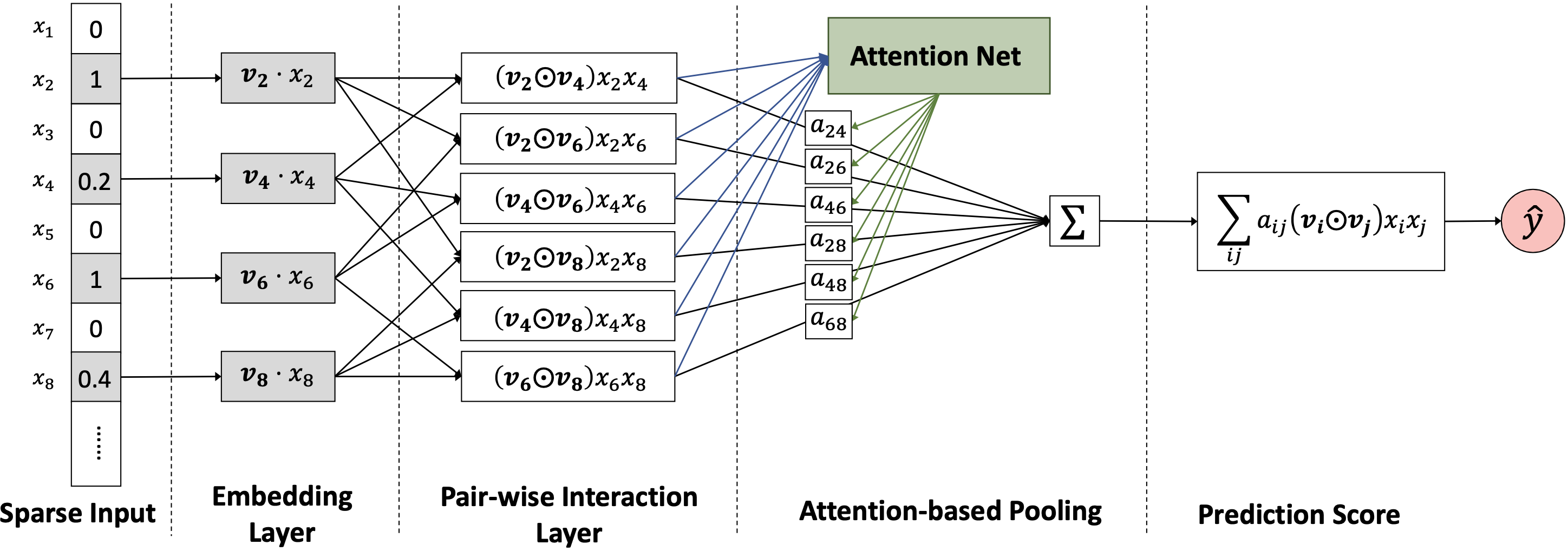
图3.2.2 AFM模型结构¶
AFM 的模型结构在 FM 的基础上进行了扩展。它首先将所有成对特征的隐向量进行元素积(Hadamard Product, 记为 :math:`odot` ),而不是像 FM 那样直接求内积。这样做保留了交叉特征的向量信息,为后续的注意力计算提供了输入。这个步骤被称为成对交互层(Pair-wise Interaction Layer)。
其中,\(\mathcal{E}\) 表示输入样本中所有非零特征的Embedding向量集合,\(\mathcal{R}_x\) 表示输入样本中所有非零特征的索引对集合。随后,模型引入一个注意力机制,来学习每个交叉特征 \((v_i \odot v_j)\) 的重要性得分 \(a_{ij}\)。
其中,\(\textbf{W}\) 是注意力网络的权重矩阵,\(\textbf{b}\) 是偏置向量,\(\textbf{h}\) 是输出层向量。这个得分 \(a_{ij}\) 经过 Softmax 归一化后,被用作加权求和的权重,与原始的交叉特征向量相乘,最终汇总成一个向量。这个过程被称为注意力池化层(Attention-based Pooling)。
最后,AFM 的完整预测公式由一阶线性部分和经过注意力加权的二阶交叉部分组成:
其中 \(\textbf{p}\) 是一个投影向量,用于将最终的交叉结果映射为标量。通过引入注意力机制,AFM 不仅提升了模型的表达能力,还通过可视化注意力权重 \(a_{ij}\) 赋予了模型更好的可解释性,让我们可以洞察哪些特征交叉对预测结果的贡献最大。
核心代码
AFM的关键在于注意力池化层,它为每个特征交叉对分配不同的权重:
# 1. 计算所有特征对的元素积交互
# group_pairwise: [batch_size, num_pairs, embedding_dim]
group_pairwise = pairwise_feature_interactions(
group_feature, drop_rate=dropout_rate
)
# 2. 注意力权重计算:h^T · ReLU(W · (v_i ⊙ v_j) + b)
weighted_inputs = tf.matmul(
group_pairwise, attention_weight
) + attention_bias # [B, num_pairs, attention_factor]
activation = tf.nn.relu(weighted_inputs)
projected = tf.matmul(activation, attention_projection) # [B, num_pairs, 1]
# 3. Softmax归一化得到注意力权重
attention_weights = tf.nn.softmax(projected, axis=1)
# 4. 加权求和:∑ a_ij · (v_i ⊙ v_j)
attention_output = tf.reduce_sum(
tf.multiply(group_pairwise, attention_weights), axis=1
) # [B, D]
相比FM对所有特征交叉一视同仁,AFM通过注意力机制自动识别重要的交互模式,提升了模型的表达能力和可解释性。
3.2.1.3. NFM: 交叉特征的深度学习¶
NFM (He and Chua, 2017) 探索了如何更深入地利用交叉信息。它将 FM 的二阶交叉结果(用哈达玛积表示的向量)作为输入,送入一个深度神经网络(DNN),从而在 FM 的基础上学习更高阶、更复杂的非线性关系。NFM 的核心思想是,FM 所捕获的二阶交叉信息本身就是一种非常有价值的特征,可以作为“原料”输入给强大的 DNN,由 DNN 来自动学习这些交叉特征之间的高阶组合关系。
NFM 的结构可以分为两个部分:先做特征交叉,再用深度网络学习。它的关键创新是引入了一个“特征交叉池化层”(Bi-Interaction Pooling Layer),这一层的作用很直接——把所有特征对的交叉信息汇总成一个向量,然后送给后面的神经网络去学习更复杂的模式。具体的计算过程如下:
其中 \(V_x = \{x_1 v_1, x_2 v_2, ..., x_n v_n\}\) 是输入样本中所有非零特征的 Embedding 向量集合,\(\odot\) 仍然是元素积操作。这个操作的结果是一个与 Embedding 维度相同的向量,它有效地编码了所有的二阶特征交叉信息。值得注意的是,与FM中的变换类似,这一层的计算同样可以被优化到线性时间复杂度,非常高效:
得到特征交叉池化层的输出向量 \(f_{BI}(V_x)\) 后,NFM 将其送入一个标准的多层前馈神经网络(MLP):
其中 \(\textbf{W}_l, \textbf{b}_l, \sigma_l\) 分别是第 \(l\) 个隐藏层的权重、偏置和非线性激活函数。最后,NFM 将一阶线性部分与 DNN 部分的输出结合起来,得到最终的预测结果:
其中 \(\textbf{h}\) 是预测层的权重向量。通过这种方式,NFM 巧妙地将 FM 的二阶交叉能力与 DNN 的高阶非线性建模能力结合在了一起。FM 可以被看作是 NFM 在没有隐藏层时的特例,这表明 NFM 是对 FM 的一个自然扩展和深度化。
核心代码
NFM的双交互池化层将所有特征对的交叉信息压缩为一个固定维度的向量,作为DNN的输入:
# 双交互池化层:1/2 * ((∑v_i)^2 - ∑(v_i^2))
# inputs: [batch_size, num_features, embedding_dim]
# (∑v_i)^2:先求和再平方
sum_of_embeds = tf.reduce_sum(inputs, axis=1) # [B, D]
square_of_sum = tf.square(sum_of_embeds) # [B, D]
# ∑(v_i^2):先平方再求和
square_of_embeds = tf.square(inputs) # [B, N, D]
sum_of_square = tf.reduce_sum(square_of_embeds, axis=1) # [B, D]
# 双交互池化输出
bi_interaction = 0.5 * (square_of_sum - sum_of_square) # [B, D]
# 送入深度神经网络
dnn_output = DNNs(
units=[64, 32], activation="relu", use_bn=True, dropout_rate=0.1
)(bi_interaction)
NFM的关键创新在于将FM的二阶交叉信息作为DNN的输入,使得模型既能捕捉特征间的交互,又能学习高阶非线性关系。
3.2.1.4. PNN: 多样化的乘积操作¶
PNN (Qu et al., 2016) 的想法很直接:既然内积(Inner Product)和元素积(Hadamard Product)都有各自的局限性,为什么不把它们结合起来呢?PNN 在内积的基础上,又引入了外积(Outer Product),希望通过多种乘积操作来更全面地捕捉特征间的交互关系。它的关键组件是“乘积层”(Product Layer),这一层会对特征 Embedding 做各种乘积运算,然后把结果传给后面的全连接网络。
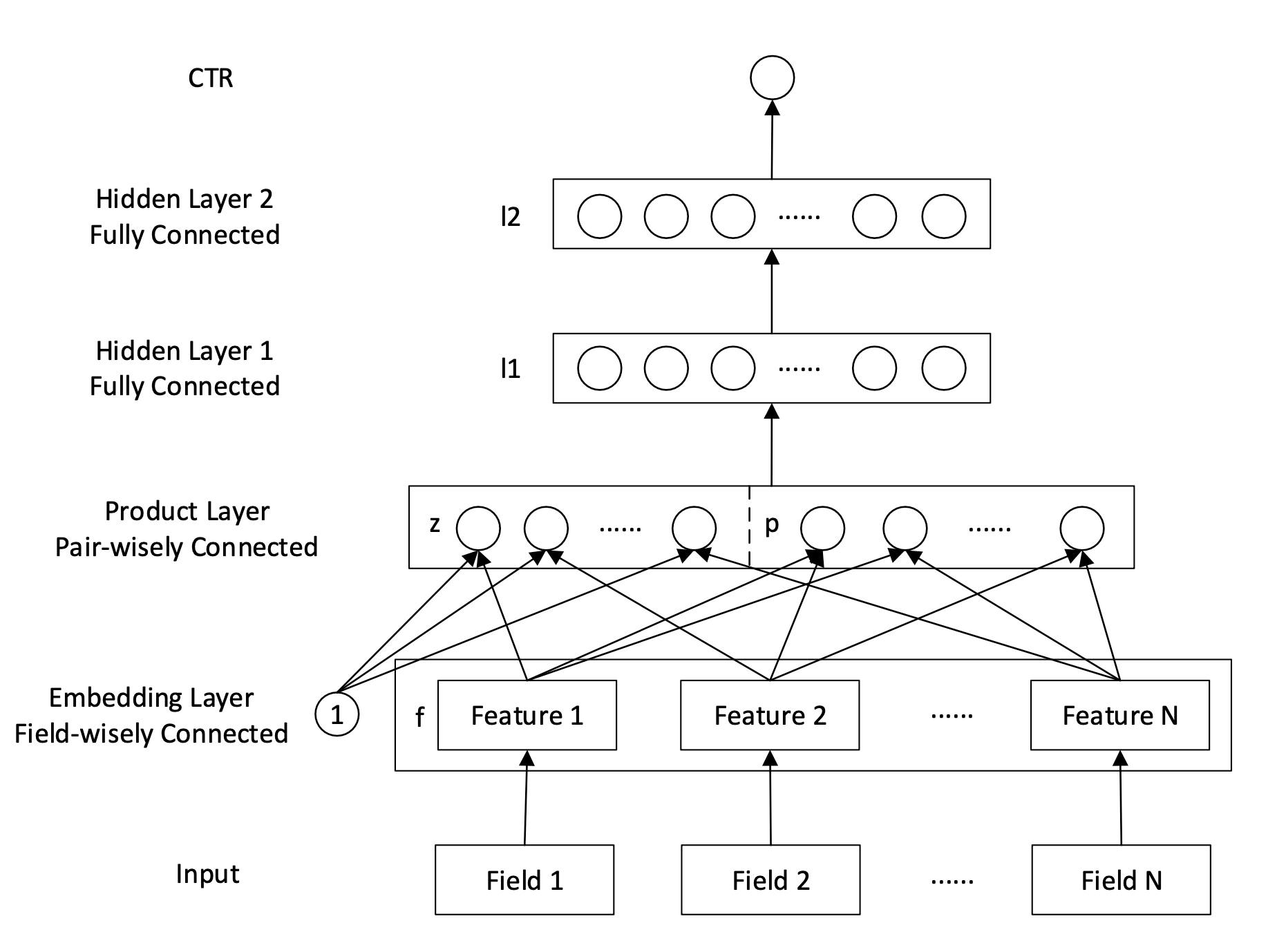
图3.2.3 PNN模型结构¶
PNN 的乘积层会产生两部分信号,一部分是线性信号 \(\mathbf{l}_z\),直接来自于各特征的 Embedding 向量,定义为:
其中 \(\mathbf{f}_i\) 是特征的 Embedding 向量,\(\mathbf{W}_z^n\) 是第 \(n\) 个神经元对应的线性信号权重矩阵。\(N\) 为特征字段数量,\(M\) 为 Embedding 维数。
另一部分是二次信号 \(\mathbf{l}_p\),来自于特征 Embedding 之间的两两交互。根据交互方式的不同,PNN 的二次信号分为两种主要的变体:
IPNN (Inner Product-based Neural Network): 这种变体使用特征 Embedding 之间的内积来计算二次信号。一个直接的计算方式是:
\(\textbf{W}_p^n\) 是第 \(n\) 个神经元对应的权重矩阵。这种计算方式的复杂度是 \(O(N^2)\),\(N\) 为特征字段数量,开销巨大。为了优化,PNN 引入了矩阵分解技巧,将权重矩阵 \(\textbf{W}_p^n\) 分解为 \(\theta_n \theta_n^T\),即 \((\textbf{W}_p^n)_{i,j} = \theta_{i,n} \theta_{j,n}\)。于是,计算过程可以被重写和简化:
通过这个变换,计算所有内积对的加权和,转变成了先对 Embedding 进行加权求和,然后计算一次向量的 L2 范数平方,复杂度成功地从 \(O(N^2M)\) 降低到了 \(O(NM)\)。
优化后的完整计算公式为:
OPNN (Outer Product-based Neural Network): 这种变体使用特征 Embedding 之间的外积 \(\mathbf{f}_i\mathbf{f}_j^T\) 来捕捉更丰富的交互信息。外积会产生一个矩阵,如果对所有外积对进行加权求和 \(\sum_{i=1}^N \sum_{j=1}^N \mathbf{f}_i \mathbf{f}_j^T\),计算复杂度会达到 \(O(N^2M^2)\)(\(M\) 为 Embedding 维数),这在实践中是不可行的。OPNN 采用了一种称为“叠加”(superposition)的近似方法来大幅降低复杂度。它不再计算所有成对的外积,而是先将所有特征的 Embedding 向量相加,然后再计算一次外积:
这样,计算量得到了节省 \(O(M(M+N))\)。优化后的完整计算公式为:
其中 对称矩阵\(\mathbf{W}_p^n \in \mathbb{R}^{M \times M}\) 是第 \(n\) 个神经元对应的权重矩阵,矩阵内积\(\langle \mathbf{A}, \mathbf{B} \rangle = \sum_{i=1}^M \sum_{j=1}^M \mathbf{A}_{i,j} \mathbf{B}_{i,j}\)。
在得到线性信号 \(l_z\) 和经过优化的二次信号 \(l_p\) 后,PNN 将它们合并,并送入后续的全连接层进行高阶非线性变换:
PNN 的独特之处在于,它将“乘积”操作(无论是内积还是外积)作为了网络中的一个核心计算单元,认为这种操作比传统 DNN 中简单的“加法”操作更能有效地捕捉类别型特征之间的交互关系。
核心代码
PNN通过内积和外积两种方式计算特征交互。以IPNN的优化实现为例:
# 线性信号:直接对特征embedding做全连接
concat_embed = tf.concat(inputs, axis=1) # [B, N*D]
lz = tf.matmul(concat_embed, linear_w) # [B, units]
# 内积优化:||∑(θ_i · f_i)||^2 代替 ∑∑<θ_i·f_i, θ_j·f_j>
lp_list = []
for i in range(units):
# 对每个特征加权:θ_i · f_i
delta = tf.multiply(
concat_embed, tf.expand_dims(inner_w[i], axis=1)
) # [B, N, D]
# 求和后计算L2范数平方:||∑(θ_i · f_i)||^2
delta = tf.reduce_sum(delta, axis=1) # [B, D]
lp_i = tf.reduce_sum(tf.square(delta), axis=1, keepdims=True) # [B, 1]
lp_list.append(lp_i)
# 拼接线性信号和内积信号
lp = tf.concat(lp_list, axis=1) # [B, units]
product_output = tf.concat([lz, lp], axis=1) # [B, 2*units]
通过矩阵分解技巧,PNN将内积计算从 \(O(N^2M)\) 优化到 \(O(NM)\),使得模型能够高效处理大规模特征交互。
3.2.1.5. FiBiNET: 特征重要性与双线性交互¶
PNN 用了多种乘积操作来做特征交互,但它把所有特征都当作同等重要。实际上,在推荐系统中,不同特征的重要性是不一样的。FiBiNET (Feature Importance and Bilinear feature Interaction Network) (Huang et al., 2019) 针对这个问题,先学习每个特征的重要性权重,再根据权重来做特征交互,最后通过双线性交互来建模特征关系。这样模型可以更有针对性地处理重要特征。
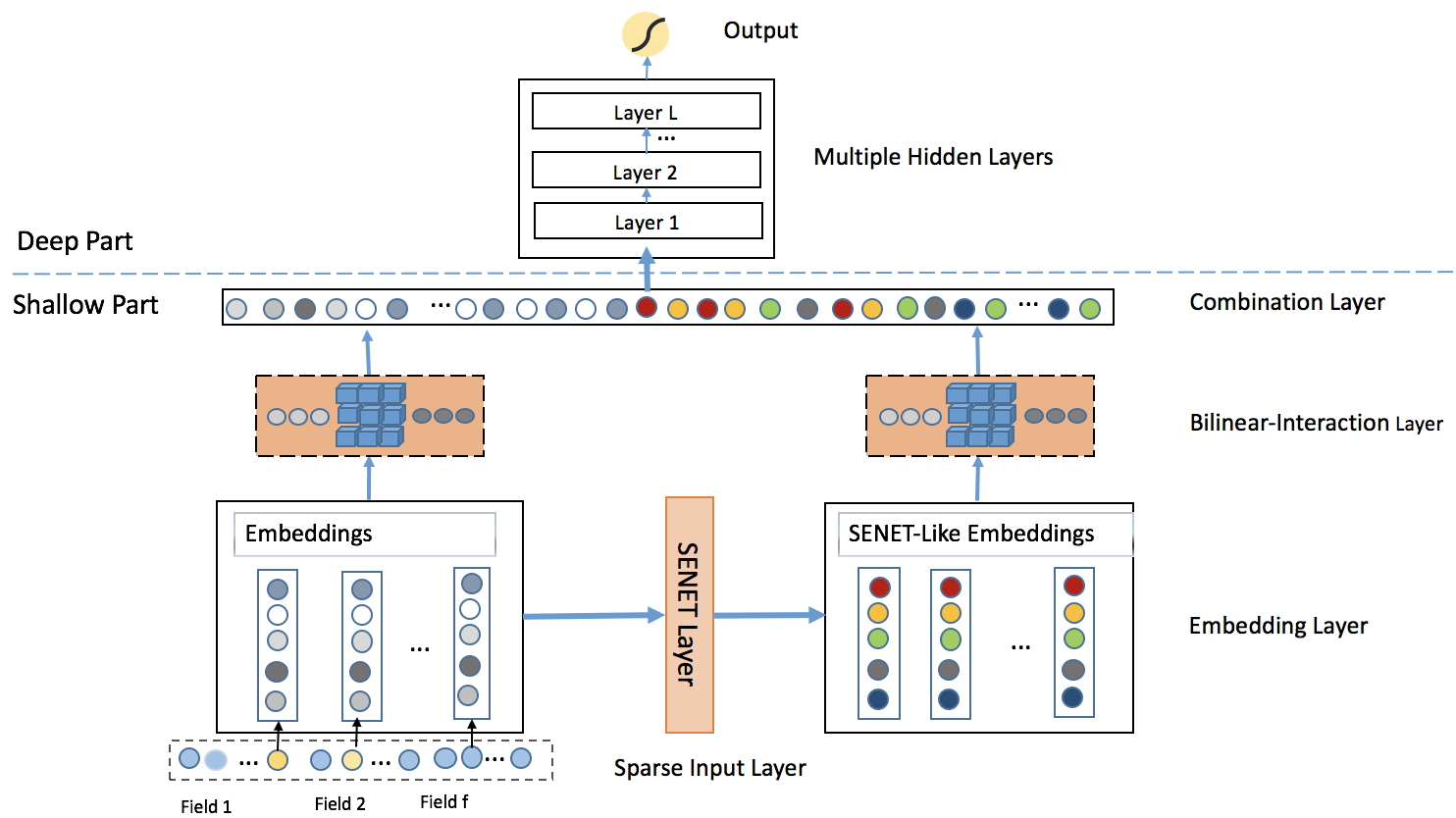
图3.2.4 FiBiNET模型结构¶
FiBiNET 的创新主要体现在两个核心模块上:SENET 特征重要性学习机制和双线性交互层。
SENET 特征重要性学习
FiBiNET 引入了来自计算机视觉领域的 SENET (Squeeze-and-Excitation Network) (Hu et al., 2018) 机制,用于动态学习每个特征的重要性权重。与传统方法对所有特征一视同仁不同,SENET 能够自适应地为不同特征分配不同的权重,让模型更加关注那些对预测任务更重要的特征。
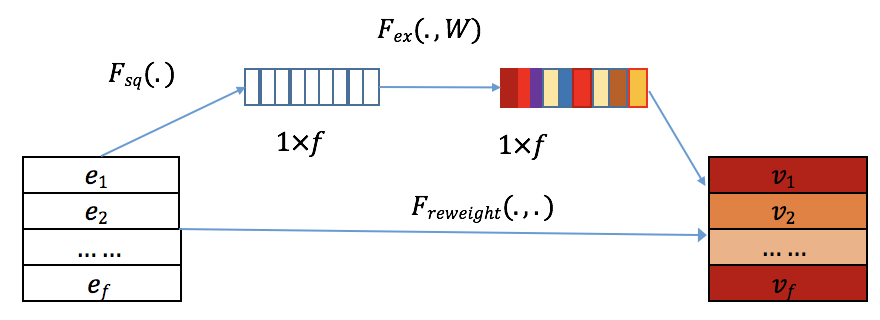
图3.2.5 SENET层结构详解¶
SENET 的工作流程分为三个步骤:
Squeeze (压缩): 把每个特征的 \(k\) 维向量 \(\mathbf{e}_i\) 压缩成一个数值,方法是计算向量的平均值:
(3.2.18)¶\[\mathbf{z}_i = F_{\text{sq}}(\mathbf{e}_i) = \frac{1}{k} \sum_{t=1}^k \mathbf{e}_i(t)\]Excitation (激活): 用两层神经网络来学习特征之间的关系,输出每个特征的重要性分数:
(3.2.19)¶\[\mathbf{A} = F_{\text{ex}}(\mathbf{Z}) = \sigma_2(\mathbf{W}_2 \sigma_1(\mathbf{W}_1 \mathbf{Z}))\]这里 \(\mathbf{W}_1 \in \mathbb{R}^{f \times \frac{f}{r}}\) 和 \(\mathbf{W}_2 \in \mathbb{R}^{\frac{f}{r} \times f}\) 是网络的权重,\(r\) 是控制网络大小的参数。
Re-weight (重新加权): 用学到的重要性分数来调整原始特征向量:
(3.2.20)¶\[\mathbf{V} = F_{\text{ReWeight}}(\mathbf{A}, \mathbf{E}) = [\mathbf{a}_1 \cdot \mathbf{e}_1, \mathbf{a}_2 \cdot \mathbf{e}_2, \ldots, \mathbf{a}_f \cdot \mathbf{e}_f]\]
双线性交互层
有了原始嵌入 \(\mathbf{E}\) 和 SENET 加权后的嵌入 \(\mathbf{V}\),FiBiNET 接下来要解决如何更好地建模特征交互的问题。传统的 FM 使用内积,PNN 使用元素积,而 FiBiNET 采用了双线性交互的方式。它引入一个可学习的变换矩阵 \(\mathbf{W} \in \mathbb{R}^{k \times k}\):
其中 \(\circ\) 表示哈达玛积。这个变换矩阵 \(\mathbf{W}\) 的作用是在计算特征交互前,先对其中一个特征向量进行线性变换,从而打破了传统方法中特征向量各维度对称交互的限制。
FiBiNET 分别对原始嵌入 \(\mathbf{E}\) 和加权嵌入 \(\mathbf{V}\) 进行双线性交互,再将两组交互结果与原始特征、深度网络输出一起送入最终的预测层。这样,FiBiNET 既考虑了特征重要性,又增强了特征交互的表达能力。
核心代码
FiBiNET的实现包含两个关键部分:SENET特征重要性学习和双线性交互。
# 1. SENET特征重要性学习
# inputs: [batch_size, num_features, embedding_dim]
# Squeeze:全局平均池化
squeeze = tf.reduce_mean(inputs, axis=-1) # [B, N]
# Excitation:两层全连接网络
excitation = tf.matmul(squeeze, w1) # [B, reduction_size]
excitation = tf.nn.relu(excitation)
excitation = tf.matmul(excitation, w2) # [B, N]
excitation = tf.nn.sigmoid(excitation)
# Re-weight:应用注意力权重
excitation = tf.expand_dims(excitation, axis=2) # [B, N, 1]
senet_output = tf.multiply(inputs, excitation) # [B, N, D]
# 2. 双线性交互:v_i · W ⊙ v_j
interaction_outputs = []
for i in range(num_features):
for j in range(i+1, num_features):
# 对特征i应用变换矩阵
vi_transformed = tf.matmul(inputs[:, i, :], W_list[idx]) # [B, D]
# 与特征j做元素积
interaction = tf.multiply(vi_transformed, inputs[:, j, :]) # [B, D]
interaction_outputs.append(interaction)
FiBiNET通过SENET动态调整特征重要性,通过双线性变换增强特征交互的表达能力,相比传统方法更加灵活和高效。
3.2.1.6. DeepFM: 低阶高阶的统一建模¶
DeepFM (Guo et al., 2017) 是对 Wide & Deep 架构的直接改进和优化。它将 Wide & Deep 中需要大量人工特征工程的 Wide 部分,直接替换为了一个无需任何人工干预的 FM 模型,从而实现了真正的端到端训练。更关键的是,DeepFM 中的 FM 组件和 Deep 组件共享同一份特征嵌入(Embedding),这带来了两大好处:首先,模型可以同时从原始特征中学习低阶和高阶的特征交互;其次,共享 Embedding 的方式使得模型训练更加高效。
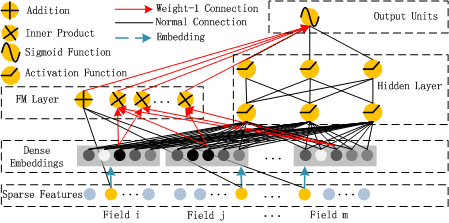
图3.2.6 DeepFM模型结构¶
DeepFM 的结构非常清晰,它由 FM 和 DNN 两个并行的组件构成,两者共享输入。
FM 组件: 负责学习一阶特征和二阶特征交叉。其输出 \(y_{FM}\) 的计算方式与标准 FM 完全相同:
这里的 \(V_{i}\) 就是特征 \(i\) 的 Embedding 向量。
Deep 组件: 负责学习高阶的非线性特征交叉。它的输入正是 FM 组件中所使用的那一套 Embedding 向量。具体来说,所有输入特征首先被映射到它们的低维 Embedding 向量上,然后这些 Embedding 向量被拼接(Concatenate)在一起,作为 DNN 的输入。
其中 \(e_i\) 是第 \(i\) 个特征字段的 Embedding 向量。这个拼接后的向量随后被送入一个标准的前馈神经网络,前向传播公式为:
其中 \(l\) 是层深度,\(\sigma\) 是激活函数,\(\textbf{W}^{(l)}\)、\(\textbf{b}^{(l)}\)分别是第 \(l\) 层的权重和偏置。最后输出为:
其中 \(H\) 是隐藏层数量.
最终,DeepFM 把 FM 部分和 Deep 部分的输出的 Logits 直接相加,再通过 Sigmoid 函数得到点击率预测:
DeepFM 的核心思路很简单:用 FM 处理低阶特征交互,用深度网络处理高阶特征交互,两者共享同一套 Embedding。这样做的好处是减少了人工特征工程的工作量,模型可以自动学习各种特征交互模式。相比 Wide & Deep 需要专家手工构造 Wide 部分的特征,DeepFM 用 FM 替代了这部分工作。
核心代码
DeepFM的关键在于FM和DNN两个组件共享同一套Embedding,各自负责不同层次的特征交互:
# 获取共享的特征embedding
# concat_feature: [batch_size, num_features, embedding_dim]
concat_feature = concat_group_embedding(
group_embedding_feature_dict, group_name, axis=1, flatten=False
)
# 1. FM组件:学习二阶特征交叉
fm_output = FM()(concat_feature) # [B, 1]
# 2. DNN组件:学习高阶非线性特征交叉
# 将embedding展平作为DNN输入
flatten_feature = tf.keras.layers.Flatten()(concat_feature) # [B, N*D]
dnn_output = DNNs(
units=[64, 32, 1], # 多层神经网络
activation="relu",
dropout_rate=0.1
)(flatten_feature) # [B, 1]
# 3. 联合训练:将FM和DNN的输出相加
deepfm_logits = tf.add(fm_output, dnn_output) # [B, 1]
output = tf.keras.layers.Dense(1, activation="sigmoid")(deepfm_logits)
DeepFM通过共享Embedding实现了端到端训练,FM组件捕捉低阶交叉,DNN组件学习高阶模式,两者互补形成高效的特征学习能力。
代码实践
from funrec import compare_models
compare_models(['fm', 'afm', 'nfm', 'pnn', 'fibinet', 'deepfm'])
+---------+--------+--------+------------+
| 模型 | auc | gauc | val_user |
+=========+========+========+============+
| fm | 0.5887 | 0.5736 | 928 |
+---------+--------+--------+------------+
| afm | 0.5784 | 0.5653 | 928 |
+---------+--------+--------+------------+
| nfm | 0.5928 | 0.5586 | 928 |
+---------+--------+--------+------------+
| pnn | 0.6001 | 0.5733 | 928 |
+---------+--------+--------+------------+
| fibinet | 0.6048 | 0.5696 | 928 |
+---------+--------+--------+------------+
| deepfm | 0.5893 | 0.577 | 928 |
+---------+--------+--------+------------+
