3.4.2. 任务依赖建模¶
前面介绍的多目标方法主要解决任务间的相关性冲突,但现实场景中任务间往往存在明确的依赖关系。用户行为具有天然的时序性:曝光→点击→转化,这种严格的依赖关系带来了新的挑战。
传统方法在处理这种依赖时面临两个核心问题:样本选择偏差(CVR模型在点击样本上训练,却要在全量样本上预测)和数据稀疏性(转化事件极其稀少)。
本节介绍两个全空间建模方法:ESMM解决经典的CTR-CVR联合建模问题,ESM2将思想扩展到更复杂的多阶段行为链路。
3.4.2.1. ESMM¶
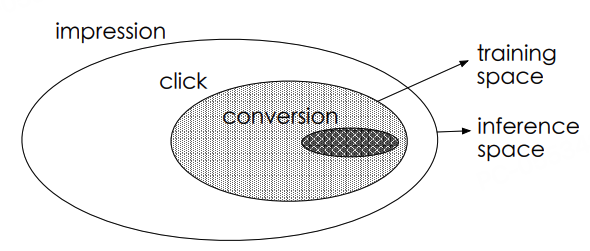
图3.4.5 点击率和转化率预估的样本空间¶
在推荐系统的用户行为链中,存在严格的时序依赖关系。以电商场景为例:
这种链式结构导致两个关键问题:
样本选择偏差(Sample Selection Bias):传统CVR模型仅在点击样本(CTR正样本)上训练,但线上预估需覆盖全量曝光样本,训练/预估样本分布差异导致泛化能力下降
数据稀疏性(Data Sparsity):转化样本量 = 曝光量 × CTR × CVR,典型场景:CTR≈2%, CVR≈0.5% → 转化样本仅为曝光的万分之一,稀疏样本难以支撑复杂模型学习
ESMM (Entire Space Multi-task Model) (Ma et al., 2018) 通过概率图约束重建任务关系:
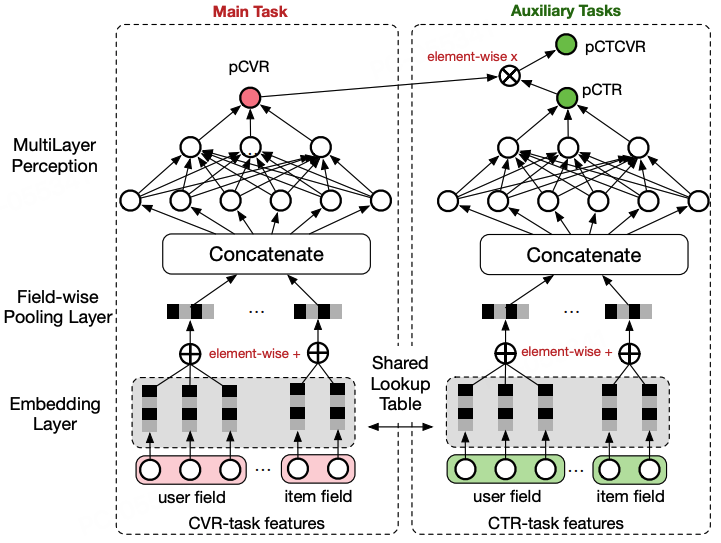
图3.4.6 ESMM模型结构¶
输入层:全量曝光样本特征 \(\mathbf{x}\)
共享表征层:基础特征提取模块(原论文中采用的是Shared-Bottom的简单共享结构,也可将其直接替换成MMoE、PLE等复杂的底层共享模型)
任务塔层:
CTR Tower:预测点击概率 \(pCTR = f_{ctr}(\mathbf{h})\)
CVR Tower:预测转化概率 \(pCVR = f_{cvr}(\mathbf{h})\)
输出层:
\(pCTR = f_{ctr}(\mathbf{h})\),\(pCVR = f_{cvr}(\mathbf{h})\),其中\(pCVR\)不用用来计算Loss
\(pCTCVR = pCTR \times pCVR\),该值用来计算从曝光空间到转化的Loss
损失函数的设计:
其中:
\(\mathcal{L}_{CTR}\) 是标准的二分类交叉熵损失,使用全量曝光样本:
(3.4.8)¶\[\mathcal{L}_{CTR} = - \frac{1}{N} \sum_{i=1}^N \left[ y_i^{click} \log(pCTR_i) + (1 - y_i^{click}) \log(1 - pCTR_i) \right]\]\(\mathcal{L}_{CTCVR}\) 是CTCVR任务的交叉熵损失, 通过概率转化公式\(pCTCVR = pCTR \times pCVR\),使得CVR Tower的参数更新是在曝光空间下进行的:
(3.4.9)¶\[\mathcal{L}_{CTCVR} = - \frac{1}{N} \sum_{i=1}^N \left[ y_i^{click} \cdot y_i^{conv} \log(pCTCVR_i) + (1 - y_i^{click} \cdot y_i^{conv}) \log(1 - pCTCVR_i) \right]\]
ESMM的核心创新在于CVR塔的梯度来源,CVR塔同时接收两种梯度:
MMOE代码实践
def build_esmm_model(
feature_columns,
task_tower_dnn_units=[128, 64],
):
# 1) 输入与嵌入:构建输入层和分组嵌入,拼接为共享 DNN 输入
input_layer_dict = build_input_layer(feature_columns)
group_embedding_feature_dict = build_group_feature_embedding_table_dict(
feature_columns, input_layer_dict, prefix="embedding/"
)
dnn_inputs = concat_group_embedding(group_embedding_feature_dict, 'dnn')
# 2) 双塔共享底座:同一输入分别走 CTR/CVR 塔,输出各自的 logit
ctr_logit = DNNs(task_tower_dnn_units + [1], name="ctr_dnn")(dnn_inputs)
cvr_logit = DNNs(task_tower_dnn_units + [1], name="cvr_dnn")(dnn_inputs)
# 3) 概率与联乘:CTR 概率,CVR 概率;CTCVR = CTR × CVR
ctr_prob = PredictLayer(name="ctr_output")(ctr_logit)
cvr_prob = PredictLayer(name="cvr_output")(cvr_logit)
ctcvr_prob = tf.keras.layers.Multiply()([ctr_prob, cvr_prob])
# 4) 构建模型:输入为所有原始输入层,输出为 [CTR, CTCVR]
model = tf.keras.Model(inputs=list(input_layer_dict.values()), outputs=[ctr_prob, ctcvr_prob])
return model
训练和评估
from funrec import run_experiment
run_experiment('esmm')
+----------------+---------------+-------------+-----------------+----------------+--------------+---------------------+--------------------+
| auc_is_click | auc_is_like | auc_macro | gauc_is_click | gauc_is_like | gauc_macro | val_user_is_click | val_user_is_like |
+================+===============+=============+=================+================+==============+=====================+====================+
| 0.5996 | 0.6939 | 0.6468 | 0.5729 | 0.5834 | 0.5782 | 928 | 530 |
+----------------+---------------+-------------+-----------------+----------------+--------------+---------------------+--------------------+
3.4.2.2. ESM2¶
ESMM成功解决了曝光→点击→转化这一两阶段行为链路的样本偏差问题,但在真实工业场景中,用户行为链路往往更长更复杂。

图3.4.7 用户下单链路图¶
如图所示,用户从曝光到转化可能会有非常多条的路径,例如
曝光->点击->加入购物车->购买、曝光->点击->加入许愿池->加入购物车->购买等。为了方便后续建模,对点击后的行为分解做了进一步的简化,将加入购物车、加入心愿单归并为决定行为(Deterministic
Action,DAction),将其余行为归并为其他行为(Other Action,OAction)

图3.4.8 简化后的用户下单链路图¶
为了更好理解后续建模时的数学表达,先对简化后图中的过程,做进一步的数学表示。
\(y_1=p(\text{点击}|\text{曝光})\)
\(y_2=p(\text{决定行为}|\text{点击})\)
\(y_3=p(\text{购买}|\text{决定行为})\)
\(y_4=p(\text{购买}|\text{其他行为})\)
根据上述定义,更便于理解ESM2模型的结构图:

图3.4.9 ESM2模型结构图¶
ESM2模型 (Wen et al., 2020)
有四个塔,分别用来预测上述的\(y_1,y_2,y_3\)和\(y_4\),对于这四个塔的输出并不是算4个Loss,而是分别计算曝光->点击、曝光->决定行为和曝光->购买这三个Loss。可以很明显的看出,这三个Loss都是在曝光空间上计算的,和ESMM在曝光空间优化CVR有着异曲同工之处。下面对于上述的三个Loss做简单的介绍,下面的\(BCE_{Loss}\)表示的是二元交叉熵损失。
\(L_{ctr}\)点击率预估损失:
\(L_{ctavr}\)点击且决定行为概率预估损失:
\(L_{ctcvr}\)转化率预估损失:
从简化后的用户下单链路图中可以看出,用户最终转化是有两条链路的,分别为:
曝光->点击->决定行为->购买=>\(y_1 \cdot y_2 \cdot y_3\)曝光->点击->其他行为->购买=>\(y_1 \cdot (1-y_2) \cdot y_4\)
合并上述两条链路的结果就可以得到\(pCTCVR=y_1(y_2 \cdot y_3 + (1-y_2) \cdot y_4)\)
最终上述三个损失通过加权融合的方式进行联合优化,
其中\(w_{ctr},w_{ctavr},w_{ctcvr}\)分别为三个损失的权重。
ESM2通过这种多阶段的概率乘积方式,将复杂的用户行为链路分解为多个可建模的子任务,同时确保每个任务都在曝光空间中进行联合优化。这种设计不仅有效解决了样本选择偏差问题,还通过共享底层特征表征,降低了数据稀疏性对模型性能的影响。更重要的是,ESM2提供了一种通用的建模思路,可以灵活扩展到更长的行为链路和更多样化的用户决策路径中。
