3.2.2. 高阶特征交叉¶

前面我们学了各种二阶特征交叉技术，这些模型能够明确地处理二阶交互，但对于更高阶的特征组合，它们主要靠深度神经网络来学习。深度网络虽然能学到高阶交互，但我们不知道它具体学到了什么，也不清楚这些交互是怎么影响预测的。所以研究者们想：能不能像 FM 处理二阶交叉那样，设计出能够明确捕捉高阶交叉的网络结构？

3.2.2.1. DCN: 残差连接的高阶交叉¶

为了解决上述问题，Deep & Cross Network (DCN) (Wang et al., 2017) 用Cross Network替代了Wide & Deep模型中的Wide部分。Cross Network在每一层都会与原始输入特征做交叉，这样就能明确地学到高阶特征交互，减少了手工特征工程的工作。

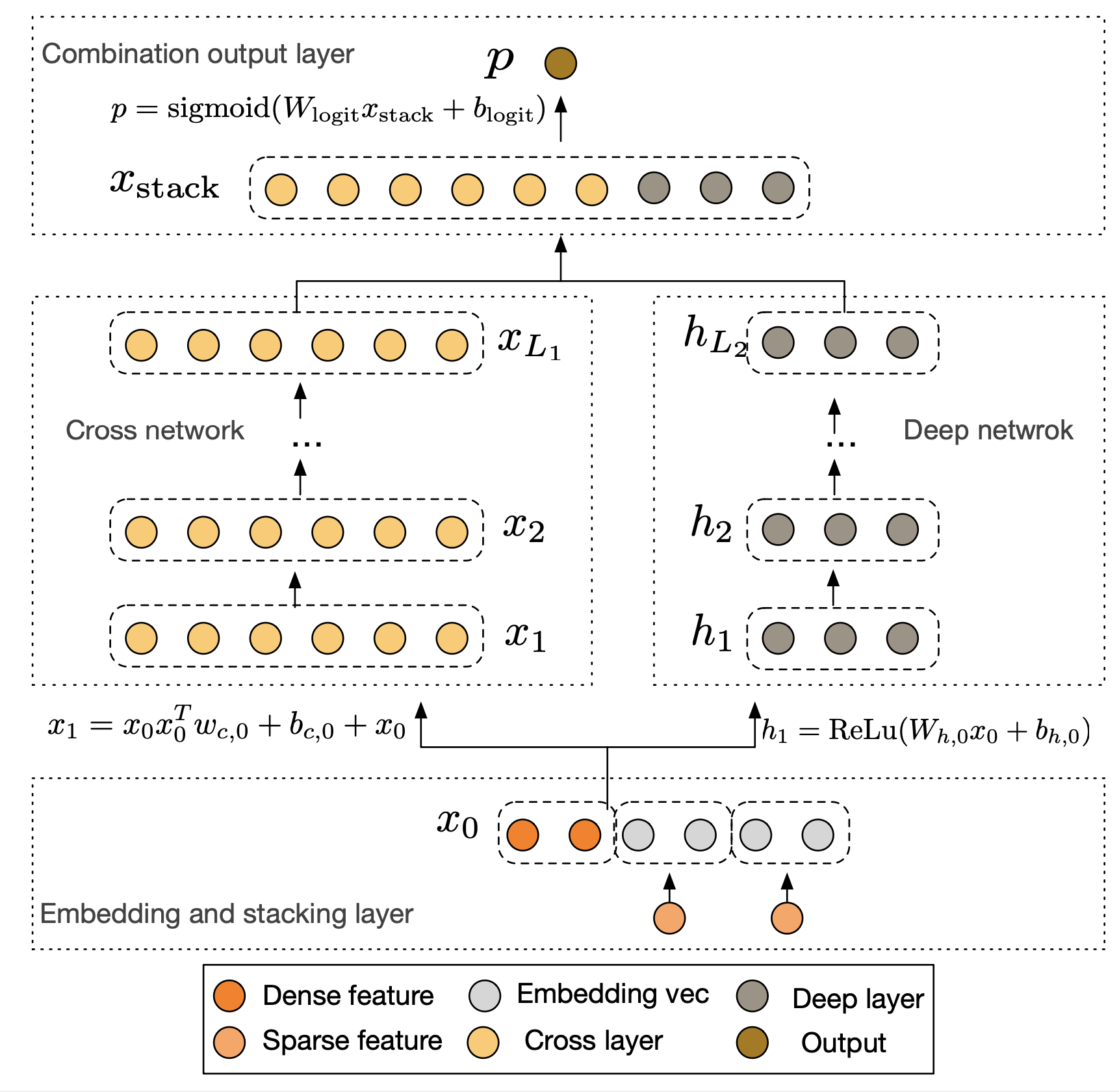
../../_images/deepcross.png — 图3.2.7 DCN模型结构¶

DCN的整体结构由并行的Cross Network和Deep Network两部分组成，它们共享相同的Embedding层输入。首先，模型将稀疏的类别特征转换为低维稠密的Embedding向量，并与数值型特征拼接在一起，形成统一的输入向量 \(\mathbf{x}_0\)。

(3.2.27)¶\[\mathbf{x}_0 = [\mathbf{x}_{\text{embed}, 1}^T, \ldots, \mathbf{x}_{\text{embed}, k}^T, \mathbf{x}_{\text{dense}}^T]\]

这个初始向量 \(\mathbf{x}_0\) 会被同时送入Cross Network和Deep Network。

Cross Network是DCN的核心创新。它由多个交叉层堆叠而成，其精妙之处在于每一层的计算都保留了与原始输入 \(\mathbf{x}_0\) 的直接交互。第 \(l+1\) 层的计算公式如下：

(3.2.28)¶\[\mathbf{x}_{l+1} = \mathbf{x}_0 \mathbf{x}_l^T \mathbf{w}_l + \mathbf{b}_l + \mathbf{x}_l\]

其中\(\mathbf{x}_l, \mathbf{x}_{l+1} \in \mathbb{R}^d\) 分别是第 \(l\) 层和第 \(l+1\) 层的输出列向量，\(\mathbf{x}_0 \in \mathbb{R}^d\) 是Cross Network的初始输入向量，\(\mathbf{w}_l, \mathbf{b}_l \in \mathbb{R}^d\) 分别是第 \(l\) 层的权重和偏置列向量。

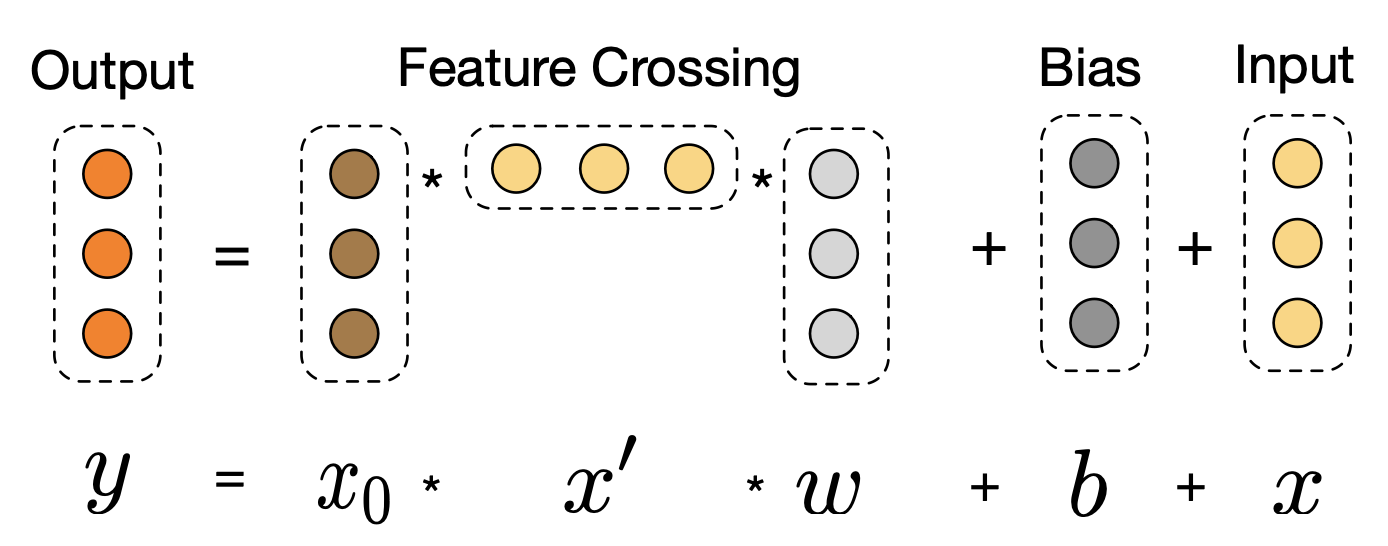
../../_images/cross_network.png — 图3.2.8 Cross Network¶

这个结构其实就是残差网络。每一层都在上一层输出 \(\mathbf{x}_l\) 的基础上，加了一个交叉项 \(\mathbf{x}_0 \mathbf{x}_l^T \mathbf{w}_l\) 和偏置项 \(\mathbf{b}_l\)。交叉项很重要，它让原始输入 \(\mathbf{x}_0\) 和当前层输入 \(\mathbf{x}_l\) 做特征交叉。层数越深，特征交叉的阶数就越高。比如第一层（\(l=0\)）时，\(\mathbf{x}_1\) 包含二阶交叉项；第二层（\(l=1\)）时，\(\mathbf{x}_1\) 本身就有二阶信息，再和 \(\mathbf{x}_0\) 交叉就产生三阶交叉项。所以Cross Network有多深，就能学到多高阶的特征交叉。而且参数量只和输入维度成正比，很高效。

与Cross Network并行的Deep Network部分是一个标准的全连接神经网络，用于隐式地学习高阶非线性关系，其结构与我们熟悉的DeepFM中的DNN部分类似。最后，模型将Cross Network的输出 \(\mathbf{x}_{L_1}\) 和Deep Network的输出 \(\mathbf{h}_{L_2}\) 拼接起来，通过一个逻辑回归层得到最终的预测概率。

(3.2.29)¶\[\mathbf{p} = \sigma([\mathbf{x}_{L_1}^T, \mathbf{h}_{L_2}^T] \mathbf{w}_{\text{logits}})\]

DCN用Cross Network明确地学习高阶特征交叉，再配合DNN学习复杂的非线性关系，这样就能更好地处理特征组合问题。

核心代码

DCN的核心在于Cross Network的交叉层计算。每一层都保持与原始输入 \(\mathbf{x}_0\) 的交叉：

# Cross Network的交叉层：x_{l+1} = x_0 * (x_l^T * w_l) + b_l + x_l
# 输入 x_0: [batch_size, feature_dim]

x_l = x_0  # 初始化为原始输入
for i in range(num_cross_layers):
    # 计算 x_l^T * w_l：得到一个标量权重
    xlw = tf.matmul(x_l, w_l)  # [B, 1]

    # 计算 x_0 * (x_l^T * w_l)：交叉项
    cross_term = tf.multiply(x_0, xlw)  # [B, D]

    # 残差连接：x_{l+1} = cross_term + b_l + x_l
    x_l = cross_term + b_l + x_l  # [B, D]

这个设计的巧妙之处在于：通过残差连接保留了原始信息，通过与 \(\mathbf{x}_0\) 的持续交叉实现了高阶特征组合，且参数量仅与输入维度线性相关。

3.2.2.2. xDeepFM: 向量级别的特征交互¶

DCN虽然能明确地学习高阶特征交叉，但它是在 元素级别(bit-wise) 上做交叉的。也就是说，Embedding向量中的每个元素都单独和其他特征的元素交互，这样就把Embedding向量拆散了，没有把它当作一个完整的特征来看待。为了解决这个问题，xDeepFM提出了压缩交互网络（Compressed Interaction Network, CIN） (Lian et al., 2018) ，改为在 向量级别(vector-wise) 上做特征交互，这样更符合我们的直觉。xDeepFM包含三个部分：线性部分、DNN部分（隐式高阶交叉）和CIN网络（显式高阶交叉），最后把三部分的输出合并得到预测结果。

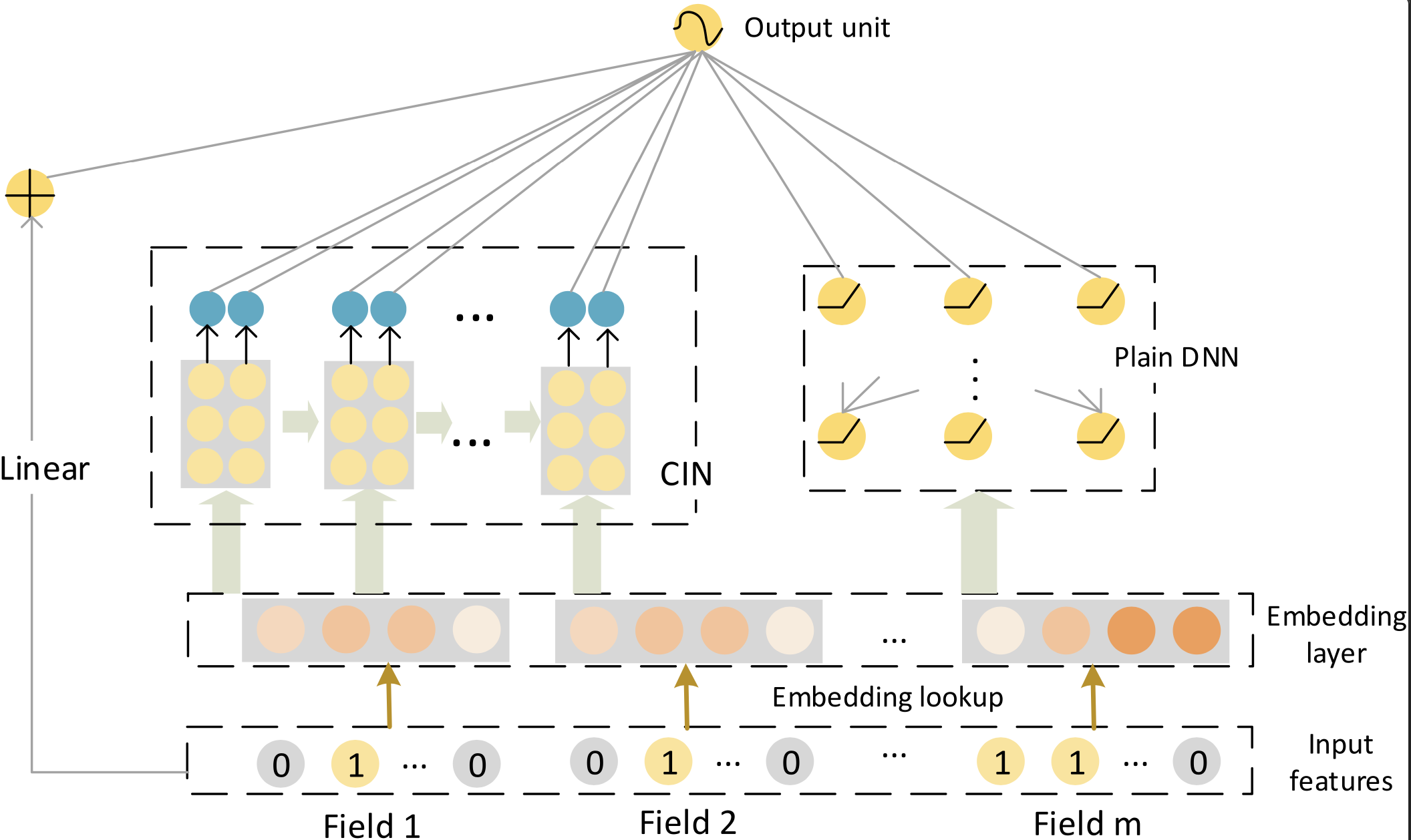
../../_images/xdeepfm.png — 图3.2.9 xdDeepFM模型架构¶

CIN的设计目标是实现向量级别的显式高阶交互，同时控制网络复杂度。它的输入是一个\(m \times D\)的矩阵 \(\mathbf{X}_0\)，其中 \(m\) 是特征域（Field）的数量，\(D\) 是Embedding的维度，矩阵的第 \(i\) 行就是第 \(i\) 个特征域的Embedding向量 \(\mathbf{e}_i\)。

CIN的计算过程在每一层都分为两步。在计算第 \(k\) 层的输出 \(\mathbf{X}_k\) 时，它依赖于上一层的输出 \(\mathbf{X}_{k-1}\) 和最原始的输入 \(\mathbf{X}_0\)。

第一步，模型计算出上一层输出的 \(H_{k-1}\) 个向量与原始输入层的 \(m\) 个向量之间的所有成对交互，生成一个中间结果。具体来说，是通过哈达玛积（Hadamard product）\(\circ\) 来实现的。这个操作会产生 \(H_{k-1} \times m\) 个交互向量，每个向量的维度仍然是 \(D\)。

第二步，为了生成第 \(k\) 层的第 \(h\) 个新特征向量 \(\mathbf{X}_{h,*}^k\)，模型对上一步产生的所有交互向量进行加权求和。这个过程可以看作是对所有潜在的交叉特征进行一次“压缩”或“提炼”。

综合起来，其核心计算公式如下：

(3.2.30)¶\[\mathbf{X}_{h,*}^k = \sum_{i=1}^{H_{k-1}} \sum_{j=1}^{m} \mathbf{W}_{i,j}^{k,h} (\mathbf{X}_{i,*}^{k-1} \circ \mathbf{X}_{j,*}^0)\]

其中：

\(\mathbf{X}_k \in \mathbb{R}^{H_k \times D}\) 是CIN第 \(k\) 层的输出，可以看作是一个包含了 \(H_k\) 个特征向量的集合，称为“特征图”。\(H_k\) 是第 \(k\) 层特征图的数量。
\(\mathbf{X}_{i,*}^{k-1}\) 是第 \(k-1\) 层输出的第 \(i\) 个 \(D\) 维向量。
\(\mathbf{X}_{j,*}^0\) 是原始输入矩阵的第 \(j\) 个 \(D\) 维向量（即第 \(j\) 个特征域的Embedding）。
\(\circ\) 是哈达玛积，它实现了向量级别的交互，保留了 \(D\) 维的向量结构。
\(\mathbf{W}_{k,h} \in \mathbb{R}^{H_{k-1} \times m}\) 是一个参数矩阵。它为每一个由 \((\mathbf{X}_{i,*}^{k-1}, \mathbf{X}_{j,*}^0)\) 产生的交互向量都提供了一个权重，通过加权求和的方式，将 \(H_{k-1} \times m\) 个交互向量的信息“压缩”成一个全新的 \(D\) 维向量 \(\mathbf{X}_{h,*}^k\)。

这个过程清晰地展示了特征交互是如何在向量级别上逐层发生的。第 \(k\) 层的输出 \(\mathbf{X}_k\) 包含了所有 \(k+1\) 阶的特征交互信息。

在计算出每一层（从第\(1\)层到第\(T\)层）的特征图 \(\mathbf{X}_k\) 后，CIN会对每个特征图 \(\mathbf{X}_k\) 的所有向量（\(H_k\)个）在维度 \(D\) 上进行求和池化（Sum Pooling），得到一个池化后的向量 \(\mathbf{p}_k \in \mathbb{R}^{H_k}\)。最后，将所有层的池化向量拼接起来，形成CIN部分的最终输出。

(3.2.31)¶\[\mathbf{p}^+ = [\mathbf{p}_1, \mathbf{p}_2, \ldots, \mathbf{p}_T]\]

这个输出 \(\mathbf{p}^+\) 捕获了从二阶到 \(T+1\) 阶的所有显式、向量级别的交叉特征信息。最终，xDeepFM将线性部分、DNN部分和CIN部分的输出结合起来，通过一个Sigmoid函数得到最终的预测结果。

(3.2.32)¶\[\hat{y} = \sigma(\mathbf{w}_{\text{linear}}^T \mathbf{a} + \mathbf{w}_{\text{dnn}}^T \mathbf{x}_{\text{dnn}}^k + \mathbf{w}_{\text{cin}}^T \mathbf{p}^+ + \mathbf{b})\]

其中\(\mathbf{a}\) 表示原始特征，\(\mathbf{x}_{\text{dnn}}^k\) 表示DNN的输出，\(\mathbf{b}\) 是可学习参数。

通过CIN网络，xDeepFM把向量级别的显式交互和元素级别的隐式交互结合到了一起，为高阶特征交互提供了一个更好的解决方案。

核心代码

CIN的核心在于向量级别的特征交互计算。每一层都通过哈达玛积实现上一层输出与原始输入的交叉：

# CIN层的向量级别交互
# inputs: [batch_size, field_num, embed_dim]

cin_layers = [inputs]  # X^0：原始输入
pooled_outputs = []

for layer_size in cin_layer_sizes:
    # 获取上一层输出 X^{k-1} 和原始输入 X^0
    x_k_minus_1 = cin_layers[-1]  # [B, H_{k-1}, D]
    x_0 = cin_layers[0]  # [B, m, D]

    # 扩展维度以便进行广播计算
    x_k_minus_1_expand = tf.expand_dims(x_k_minus_1, axis=2)  # [B, H_{k-1}, 1, D]
    x_0_expand = tf.expand_dims(x_0, axis=1)  # [B, 1, m, D]

    # 向量级别的哈达玛积交互
    z_k = tf.multiply(x_k_minus_1_expand, x_0_expand)  # [B, H_{k-1}, m, D]

    # 压缩：通过线性变换将 H_{k-1}*m 个交互向量压缩为 H_k 个
    z_k_reshape = tf.reshape(z_k, [batch_size, -1, embed_dim])  # [B, H_{k-1}*m, D]
    x_k = dense_layer(tf.transpose(z_k_reshape, [0, 2, 1]))  # [B, D, H_k]
    x_k = tf.transpose(x_k, [0, 2, 1])  # [B, H_k, D]

    cin_layers.append(x_k)

    # 求和池化：将向量维度聚合为标量
    pooled_outputs.append(tf.reduce_sum(x_k, axis=-1))  # [B, H_k]

# 拼接所有层的输出
cin_output = tf.concat(pooled_outputs, axis=1)  # [B, sum(H_k)]

CIN通过保持向量结构的交互方式，既实现了显式的高阶特征组合，又避免了参数量的过快增长。

3.2.2.3. AutoInt: 自注意力的自适应交互¶

DCN用残差连接做元素级别的高阶交互，xDeepFM用CIN网络做向量级别的高阶交互，但这两种方法都有个问题：交互方式比较固定。DCN每一层都要和原始输入交叉，xDeepFM的CIN网络也是按固定方式做向量交互。那么，能不能设计一种更灵活的高阶特征交互方法，让模型自己决定哪些特征要交互，交互强度多大？

AutoInt (Automatic Feature Interaction) (Song et al., 2019) 通过Transformer的自注意力机制，让模型自动学习各种阶数的特征交互。和前面的方法不同，AutoInt不用固定的交互模式，而是在训练中学出最好的特征交互组合。

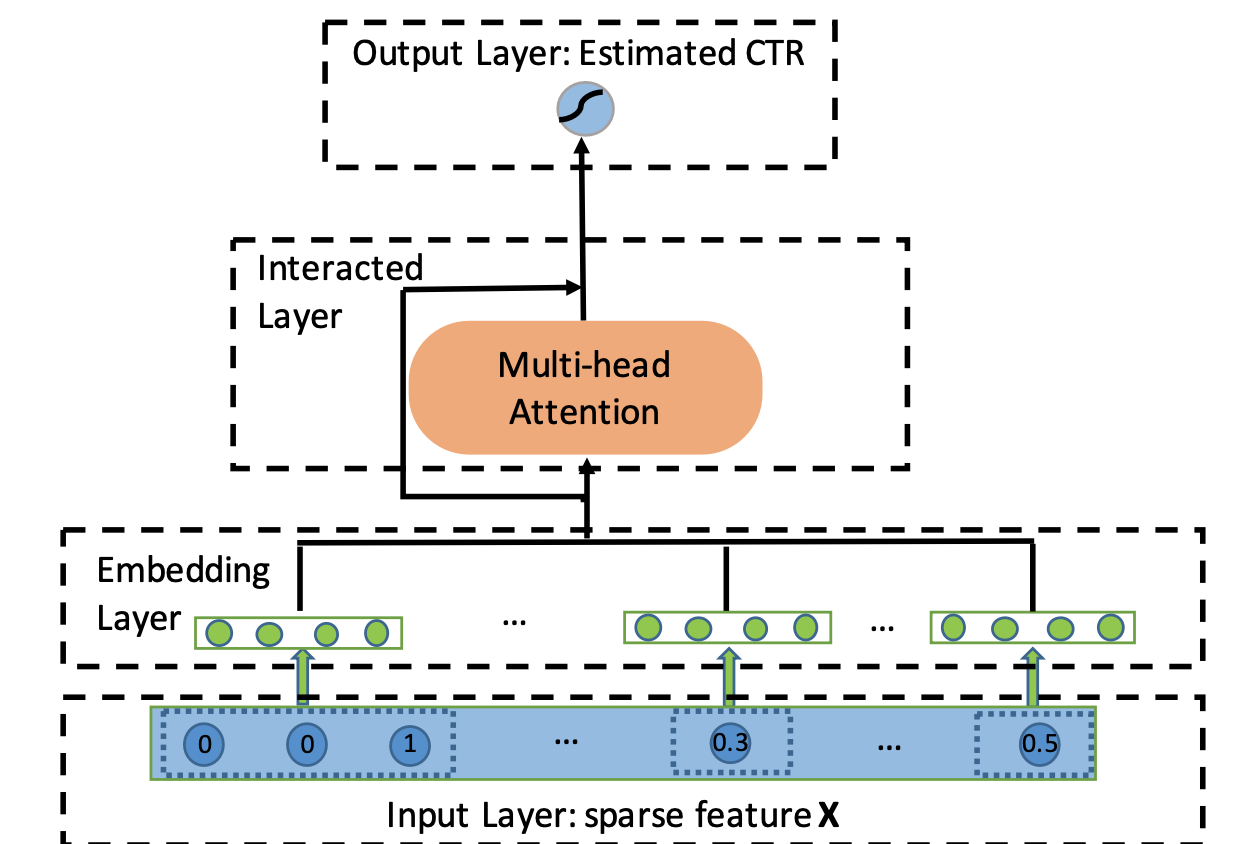
../../_images/autoint_overview.png — 图3.2.10 AutoInt模型原理示意图¶

AutoInt 的整体架构相对简洁，它将所有输入特征（无论是类别型还是数值型）都转换为相同维度的嵌入向量 \(\mathbf{e}_m \in \mathbb{R}^d\)，其中 \(m\) 代表第 \(m\) 个特征域。这些嵌入向量构成了自注意力网络的输入，类似于 Transformer 中的 Token Embeddings。

多头自注意力机制

AutoInt 的核心是其交互层，该层由多头自注意力机制构成。对于任意两个特征的嵌入向量 \(\mathbf{e}_m\) 和 \(\mathbf{e}_k\)，自注意力机制会计算它们之间的相关性得分。这个过程在每个“注意力头”（Head） \(h\) 中独立进行。具体来说，对于特征 \(m\) 和特征 \(k\)，它们在第 \(h\) 个注意力头中的相关性得分 \(\alpha_{m,k}^{(h)}\) 计算如下：

(3.2.33)¶\[\alpha_{m,k}^{(h)} = \frac{\exp(\psi^{(h)}(\mathbf{e}_m, \mathbf{e}_k))}{\sum_{l=1}^{M}\exp(\psi^{(h)}(\mathbf{e}_m, \mathbf{e}_l))}\]

这里的 \(M\) 是特征域的总数，而 \(\psi^{(h)}(\mathbf{e}_m, \mathbf{e}_k)\) 是一个用于衡量两个嵌入向量相似度的函数，通常是缩放点积注意力：

(3.2.34)¶\[\psi^{(h)}\left(\mathbf{e}_{\mathbf{m}}, \mathbf{e}_{\mathbf{k}}\right)=\left\langle\mathbf{W}_{\text {Query }}^{(h)} \mathbf{e}_{\mathbf{m}}, \mathbf{W}_{\text {Key }}^{(h)} \mathbf{e}_{\mathbf{k}}\right\rangle\]

其中 \(\mathbf{W}_{\text{Query}}^{(h)} \in \mathbb{R}^{d' \times d}\) 和 \(\mathbf{W}_{\text{Key}}^{(h)} \in \mathbb{R}^{d' \times d}\) 是可学习的投影矩阵，它们分别将原始嵌入向量映射到“查询”（Query）和“键”（Key）空间。\(d'\) 是投影后的维度。

在计算出所有特征对之间的相关性得分后，模型会利用这些得分来对所有特征的“值”（Value）向量进行加权求和，从而为特征 \(\mathbf{e}_m\) 生成一个新的、融合了其他特征信息的表示 \(\mathbf{\tilde{e}}_m^{(h)}\)：

(3.2.35)¶\[\mathbf{\tilde{e}}_m^{(h)} = \sum_{k=1}^{M} \alpha_{m,k}^{(h)} (\mathbf{W}_{\text{Value}}^{(h)} \mathbf{e}_k)\]

其中 \(\mathbf{W}_{\text{Value}}^{(h)} \in \mathbb{R}^{d' \times d}\) 同样是一个可学习的投影矩阵。这个新的表示 \(\mathbf{\tilde{e}}_m^{(h)}\) 本质上就是一个通过自适应学习得到的新组合特征。

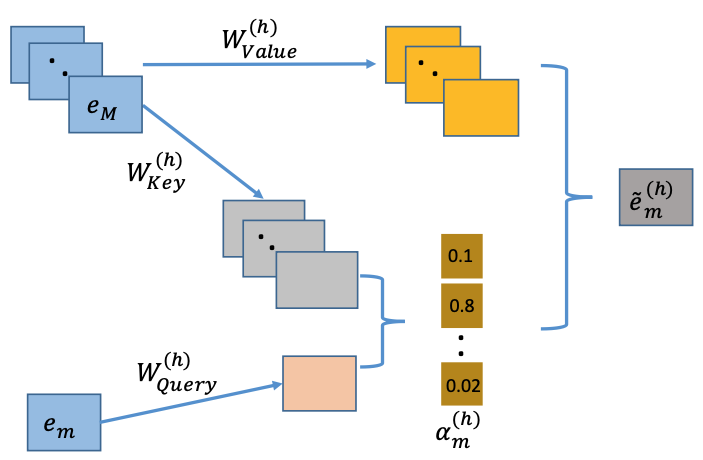
../../_images/autoint_attention.png — 图3.2.11 自注意力机制示意图¶

多层交互与高阶特征学习

“多头”机制允许模型在不同的子空间中并行地学习不同方面的特征交互。模型将所有 \(H\) 个头的输出拼接起来，形成一个更丰富的特征表示：

(3.2.36)¶\[\mathbf{\tilde{e}}_m = \mathbf{\tilde{e}}_m^{(1)} \oplus \mathbf{\tilde{e}}_m^{(2)} \oplus \cdots \oplus \mathbf{\tilde{e}}_m^{(H)}\]

其中 \(\oplus\) 表示拼接操作。为了保留原始信息并稳定训练过程，AutoInt 还引入了残差连接（Residual Connection），将新生成的交互特征与原始特征相结合：

(3.2.37)¶\[\mathbf{e}_m^{\text{Res}}= \text{ReLU}(\mathbf{e}_m + \mathbf{W}_{\text{Res}} \mathbf{\tilde{e}}_m)\]

其中 \(\mathbf{W}_{\text{Res}}\) 是一个用于匹配维度的投影矩阵。

AutoInt 的关键创新在于其高阶特征交互的构建方式。通过堆叠多个这样的交互层，AutoInt 能够显式地构建任意高阶的特征交互。第一层的输出包含了二阶交互信息，第二层的输出则包含了三阶交互信息，以此类推。每一层的输出都代表了更高一阶的、自适应学习到的特征组合。与 DCN 和 xDeepFM 不同，AutoInt 中的高阶交互不是通过固定的数学公式构建的，而是通过注意力权重动态决定的，这使得模型能够学习到更加灵活和有效的特征交互模式。

最终，所有层输出的特征表示被拼接在一起，送入一个简单的逻辑回归层进行最终的点击率预测：

(3.2.38)¶\[\hat{y}=\sigma\left(\mathbf{w}^{\mathrm{T}}\left(\mathbf{e}_{1}^{\mathbf{Res}} \oplus \mathbf{e}_{2}^{\mathbf{Res}} \oplus \cdots \oplus \mathbf{e}_{\mathbf{M}}^{\text {Res}}\right)+b\right)\]

AutoInt 的一个好处是比较好解释，通过看注意力权重矩阵 \(\alpha^{(h)}\)，我们能直接看出模型觉得哪些特征组合重要。这种用自注意力做高阶特征交互的方法，不仅让模型表达能力更强，还提供了一种更灵活的学习方式。

核心代码

AutoInt的核心在于多头自注意力机制，它能够自适应地学习特征之间的交互关系：

# 多头自注意力层的前向传播
# inputs: [batch_size, num_features, embed_dim]

head_outputs = []
for i in range(num_heads):
    # 计算Query、Key、Value矩阵
    query = tf.einsum('bfe,ea->bfa', inputs, query_weights[i])  # [B, N, d']
    key = tf.einsum('bfe,ea->bfa', inputs, key_weights[i])      # [B, N, d']
    value = tf.einsum('bfe,ea->bfa', inputs, value_weights[i])  # [B, N, d']

    # 计算注意力得分：Query和Key的点积
    attention_score = tf.matmul(query, key, transpose_b=True)  # [B, N, N]

    # Softmax归一化得到注意力权重
    attention_weights = tf.nn.softmax(attention_score, axis=-1)  # [B, N, N]

    # 加权求和：用注意力权重对Value进行聚合
    head_output = tf.matmul(attention_weights, value)  # [B, N, d']
    head_outputs.append(head_output)

# 拼接多个注意力头的输出
multi_head_output = tf.concat(head_outputs, axis=-1)  # [B, N, d'*H]

# 残差连接：保留原始信息
residual_input = tf.tensordot(inputs, residual_weights, axes=[[2], [0]])
output = tf.keras.layers.ReLU()(multi_head_output + residual_input)

通过堆叠多层这样的自注意力层，AutoInt能够显式地构建任意高阶的特征交互，且交互模式完全由数据驱动学习得到。

代码实践

from funrec import compare_models

compare_models(['dcn', 'xdeepfm', 'autoint'])

+---------+--------+--------+------------+
| 模型    |    auc |   gauc |   val_user |
+=========+========+========+============+
| dcn     | 0.5968 | 0.574  |        928 |
+---------+--------+--------+------------+
| xdeepfm | 0.5964 | 0.5741 |        928 |
+---------+--------+--------+------------+
| autoint | 0.5988 | 0.571  |        928 |
+---------+--------+--------+------------+