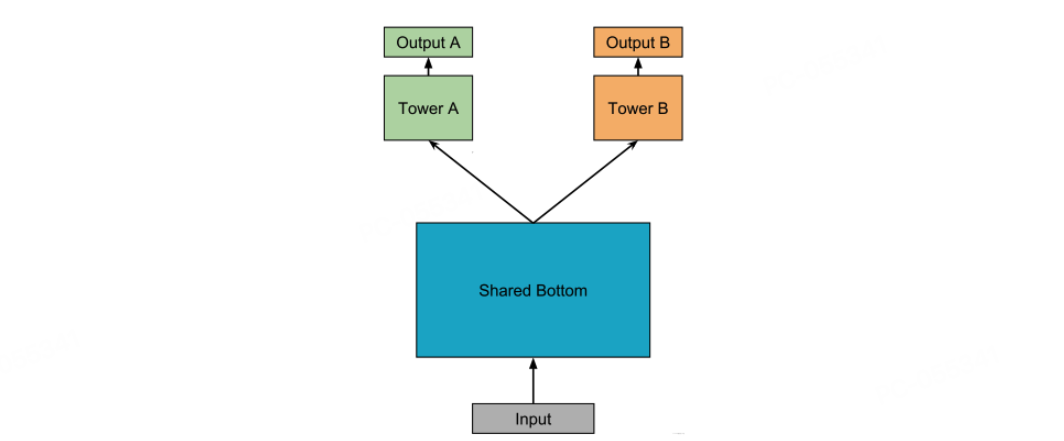
3.4.1. 基础结构演进

3.4.1.1. Shared-Bottom

Shared-Bottom (Caruana, 1997) 模型作为多目标建模的奠基性架构，采用“共享地基+独立塔楼”的设计范式。其核心结构包含两个关键组件：

  • 共享底层（Shared Bottom）：所有任务共用同一组特征转换层，负责学习跨任务的通用特征表示；

  • 任务特定塔（Task-Specific Towers）：每个任务拥有独立的顶层网络，基于共享表示学习任务特定决策边界。

../../_images/shared-bottom.png

图3.4.1 Shared-Bottom

这种架构的数学表达可描述为：

(3.4.1)\[\hat{y}_t = f_t(W_t \cdot g(W_s \mathbf{x}))\]

其中 \(\mathbf{W}_s\) 为共享层参数，\(g(\cdot)\) 为共享特征提取函数，\(f_t(\cdot)\) 为任务 \(t\) 的预测函数。其设计哲学建立在任务同质性假设上：不同任务共享相同的底层特征空间，仅需在顶层进行任务适配。

Shared-Bottom 模型在效率与泛化之间实现了良好的平衡，其核心优势主要体现在以下几点。

  1. 在参数效率方面，共享层占据了模型大部分的参数量这显著降低了模型的总参数量。

  2. 共享层具有正则化效应，它如同一个天然的正则化器，通过强制任务共用特征表示，有效防止了单个任务出现过拟合的情况。

  3. 在知识迁移方面，当任务之间存在潜在的相关性时，例如视频的点击率与完播率，共享层能够学习到通用的模式，从而提升小样本任务的泛化能力。

然而，Shared-Bottom 模型也存在一个致命缺陷，即负迁移现象。当任务之间存在本质上的冲突时，该模型的硬共享机制会引发负迁移问题。从机制本质上来看，共享层的梯度更新方向是由所有任务共同决定的，一旦任务目标之间出现冲突，参数优化就会陷入方向性的矛盾。

在一些典型场景中，例如电商平台同时优化“点击率”与“客单价”时，低价商品可能会推动点击率的提升，但同时却抑制了客单价的增长；又如内容平台在平衡“内容消费深度”与“广告曝光量”时，深度阅读行为往往与广告点击行为呈负相关。

从数学角度来解释，假设任务\(i\)与任务\(j\)的损失梯度分别为\(\nabla L_i\)与\(\nabla L_j\)，当\(\nabla L_i \cdot \nabla L_j\) < 0时，共享层参数更新就会产生内在的冲突。这种冲突使得模型在处理矛盾任务时呈现出“零和博弈”的特性，即提升某一目标的性能往往需要以牺牲另一目标为代价，我们一般也称这类问题为跷跷板问题。

Shared-Bottom代码实践

shared-bottom模型构建代码如下，先组装输入到shared-bottom网络中的特征dnn_inputs, 经过一个shared-bottom DNN网络，遍历创建各个任务独立的DNN塔，最后输出多个塔的预估值用于计算Loss。

def build_shared_bottom_model(
        feature_columns,
        task_name_list,
        share_dnn_units=[128, 64],
        task_tower_dnn_units=[128, 64],
        ):
    # 输入层：将原始特征映射为 Keras 输入
    input_layer_dict = build_input_layer(feature_columns)

    # 嵌入层：为各特征组创建嵌入表，得到组内嵌入向量
    embedding_table_dict = build_group_feature_embedding_table_dict(
        feature_columns, input_layer_dict, prefix="embedding/"
    )

    # 合并嵌入：将多组嵌入拼接为共享 DNN 的输入
    dnn_inputs = concat_group_embedding(embedding_table_dict, 'dnn')

    # 共享底座：所有任务共享的特征抽取网络（Shared Bottom）
    shared_feature = DNNs(share_dnn_units)(dnn_inputs)

    # 任务塔：在共享特征上为每个任务构建独立塔并输出概率
    task_outputs = []
    for task_name in task_name_list:
        task_logit = DNNs(task_tower_dnn_units + [1])(shared_feature)
        task_prob = PredictLayer(name=f"task_{task_name}")(task_logit)
        task_outputs.append(task_prob)

    # 构建多任务模型：共享底座 + 多任务塔输出
    model = tf.keras.Model(inputs=list(input_layer_dict.values()), outputs=task_outputs)
    return model

训练和评估

from funrec import run_experiment

run_experiment('shared_bottom')

+----------------+---------------+-----------------+-------------+-----------------+----------------+------------------+--------------+---------------------+--------------------+----------------------+
|   auc_is_click |   auc_is_like |   auc_long_view |   auc_macro |   gauc_is_click |   gauc_is_like |   gauc_long_view |   gauc_macro |   val_user_is_click |   val_user_is_like |   val_user_long_view |
+================+===============+=================+=============+=================+================+==================+==============+=====================+====================+======================+
|           0.61 |         0.431 |          0.4364 |      0.4925 |          0.5727 |         0.4433 |           0.4438 |       0.4866 |                 928 |                530 |                  925 |
+----------------+---------------+-----------------+-------------+-----------------+----------------+------------------+--------------+---------------------+--------------------+----------------------+

3.4.1.2. MMoE

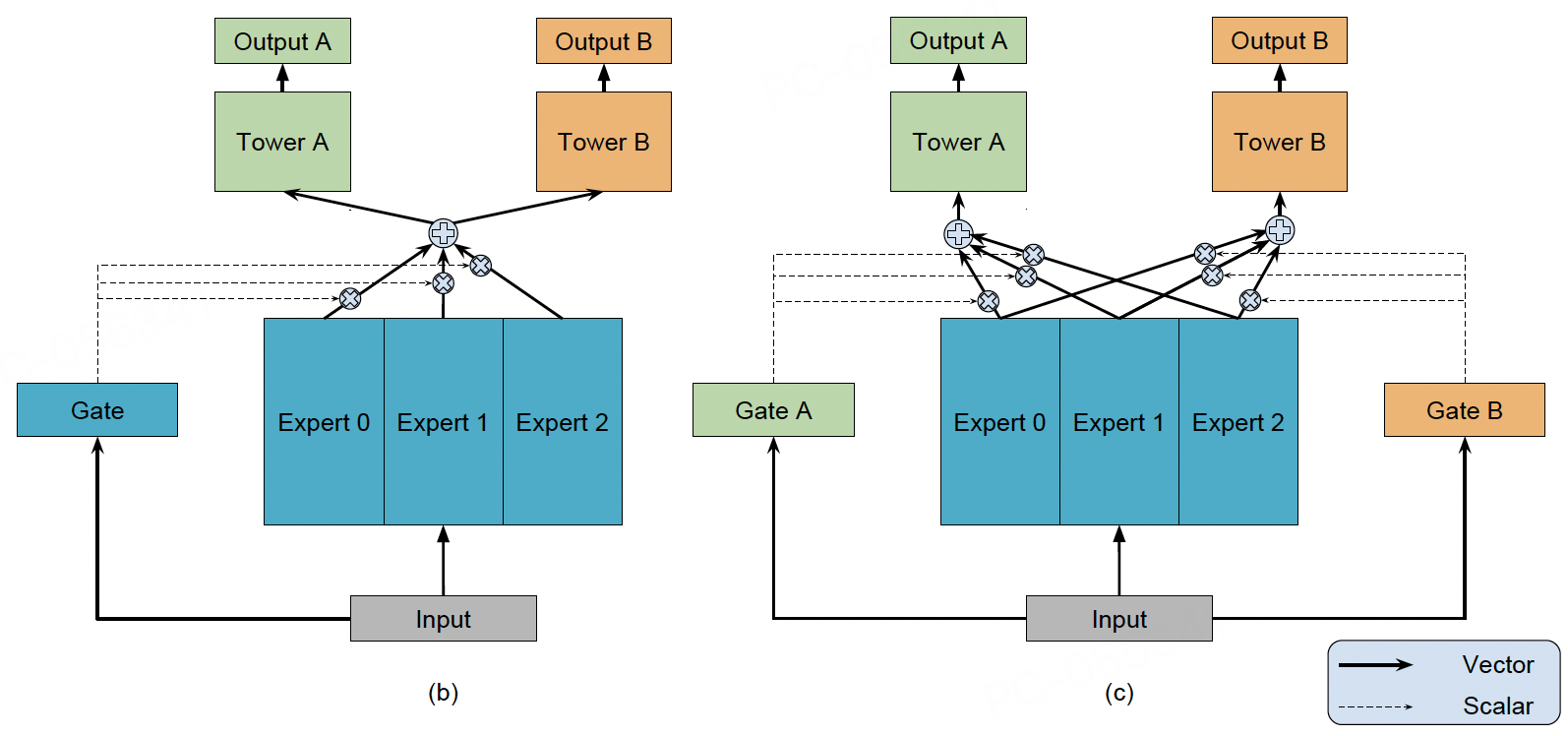
../../_images/mmoe.png

图3.4.2 MMoE模型结构

针对Shared-Bottom对相关性低的多个任务出现负迁移的现象，OMoE（OneGate Mixture-of-Experts）将底层共享的一个Shared-Bottom模块拆分成了多个Expert，最终OMoE的输出为多个Expert的加权和，本质可以看成是专家网络和全局门控的双层结构。

虽然OMoE通过底层多专家融合的方式提升了特征表征的多样性，从最终的实验结果看，确实可以一定程度上缓解低相关性任务的负迁移问题，但没有彻底解决多任务冲突的问题。因为不同任务反向传播的梯度还是会直接影响底层专家网络的学习。

为了进一步缓解多任务冲突，MMoE（Multi-gate Mixture-of-Experts）:cite:ma2018modeling 为每个任务配备专属门控网络，实现了门控从“全局共享”升级为“任务自适应”的方式。MMoE的数学表达式可以表示为：

(3.4.2)\[\begin{split}\begin{aligned} \mathbf{e}_k &= f_k(\mathbf{x}) \\ g_t(\mathbf{x}) &= \text{softmax}(\mathbf{W}_t \mathbf{x}) \\ \mathbf{h}_t &= \sum_{k=1}^K g_{t,k} \cdot \mathbf{e}_k \\ \hat{y}_t &= f_t(\mathbf{h}_t) \end{aligned}\end{split}\]

其中 \(\mathbf{x}\)表示底层的特征输入， \(\mathbf{e}_k\)表示第k个专家网络的输出， \(g_t(\mathbf{x})\)表示第\(t\)个任务融合专家网络的门控向量， \(\mathbf{h}_t\)表示第\(t\)个任务融合专家网络的输出，\(\hat{y}_t\)表示第\(t\)个任务的预测结果。

差异化特征融合门控网络\(g_t\)根据任务特性选择专家组合，例如在电商场景，CTR任务门控加权“即时兴趣”“价格敏感”专家，CVR任务门控：侧重“消费能力”“品牌忠诚”专家。

当任务\(i\)与\(j\)冲突时，MMoE的门控机制会让两个任务学习到不同专家的权重分布。例如，某个专家\(e_m\)可能在任务\(i\)的门控网络中获得很高的权重\(g_{i,m}\)，而在任务\(j\)的门控网络中获得很低的权重\(g_{j,m}\)。这样一来，专家\(e_m\)的参数更新主要由任务\(i\)的梯度决定，而任务\(j\)的梯度影响很小，从而实现了梯度隔离。不同任务通过选择不同的专家组合，可以各自学习到适合自己的特征表示，缓解任务冲突。

MMoE代码实践

MMoE模型构建代码如下，先组装输入到MoE网络中的特征dnn_inputs, 然后为每个任务创建一个门控网络输出最终融合专家网络的门控向量。最后为每个任务都创建一个任务塔，并且不同任务塔的输入都是对应任务的门控向量和多个专家网络融合后的向量。

def build_mmoe_model(
        feature_columns,
        task_name_list,
        expert_nums=4,
        expert_dnn_units=[128, 64],
        gate_dnn_units=[128, 64],
        task_tower_dnn_units=[128, 64],
        ):
    # 输入层：原始特征 → Keras 输入
    input_layer_dict = build_input_layer(feature_columns)

    # 嵌入层：为各特征组创建嵌入表，得到组内嵌入向量
    embedding_table_dict = build_group_feature_embedding_table_dict(
        feature_columns, input_layer_dict, prefix="embedding/"
    )

    # 合并嵌入：拼接为专家与门控的共同输入
    dnn_inputs = concat_group_embedding(embedding_table_dict, 'dnn')

    # 共享专家：多个并行 DNN（专家）供所有任务共享
    expert_outputs = [DNNs(expert_dnn_units, name=f"expert_{i}")(dnn_inputs)
                      for i in range(expert_nums)]
    # 形状 [B, E, D]：按专家维度堆叠，便于后续加权求和
    experts = tf.keras.layers.Lambda(lambda xs: tf.stack(xs, axis=1))(expert_outputs)

    # 任务门控：每个任务产生 softmax 权重，对专家加权融合
    task_features = []
    for idx, task_name in enumerate(task_name_list):
        gate_hidden = DNNs(gate_dnn_units, name=f"task_{idx}_gate_mlp")(dnn_inputs)
        gate_weights = tf.keras.layers.Dense(expert_nums, use_bias=False,
                                             activation='softmax',
                                             name=f"task_{idx}_gate_softmax")(gate_hidden)  # [B, E]
        # 加权融合：einsum('be,bed->bd') == sum_e w_e * expert_e
        task_mix = tf.keras.layers.Lambda(lambda x: tf.einsum('be,bed->bd', x[0], x[1]))([gate_weights, experts])
        task_features.append(task_mix)

    # 任务塔：基于融合特征为每个任务建塔并输出概率
    task_outputs = []
    for task_name, task_feat in zip(task_name_list, task_features):
        task_logit = DNNs(task_tower_dnn_units + [1])(task_feat)
        task_prob = PredictLayer(name=f"task_{task_name}")(task_logit)
        task_outputs.append(task_prob)

    # 构建模型：共享专家 + 任务门控 + 任务塔
    model = tf.keras.Model(inputs=list(input_layer_dict.values()), outputs=task_outputs)
    return model

训练和评估

run_experiment('mmoe')

+----------------+---------------+-----------------+-------------+-----------------+----------------+------------------+--------------+---------------------+--------------------+----------------------+
|   auc_is_click |   auc_is_like |   auc_long_view |   auc_macro |   gauc_is_click |   gauc_is_like |   gauc_long_view |   gauc_macro |   val_user_is_click |   val_user_is_like |   val_user_long_view |
+================+===============+=================+=============+=================+================+==================+==============+=====================+====================+======================+
|         0.6036 |        0.4203 |          0.4586 |      0.4942 |          0.5728 |         0.4362 |           0.4759 |        0.495 |                 928 |                530 |                  925 |
+----------------+---------------+-----------------+-------------+-----------------+----------------+------------------+--------------+---------------------+--------------------+----------------------+

3.4.1.3. PLE

MMoE 通过为每个任务配备专属门控网络，在一定程度上缓解了多任务冲突问题。专属门控网络能够根据任务特性选择专家组合，从而使得不同任务可以关注不同的特征表示。但其架构仍存在一个根本性局限：所有专家对所有任务门控可见。这种“软隔离”设计在实践中仍面临两大挑战：

  1. 负迁移未根除：

    • 干扰路径未切断：即使某个专家（如\(e_m\)）被任务\(i\)的门控高度加权而被任务\(j\)的门控忽略，任务\(j\)的梯度在反向传播时仍会流经\(e_m\)（因为\(e_m\)是任务\(j\)门控的可选项）。当任务冲突强烈时，这种“潜在通路”仍可能导致共享表征被污染。

    • 专家角色模糊：MMoE缺乏机制强制专家明确分工。一个专家可能同时承载共享信息和多个任务的特定信息，成为冲突的“重灾区”。尤其在任务相关性低时，这种耦合会加剧负迁移。

  2. 门控决策负担重：

    • 每个任务的门控需要在所有\(K\)个专家上进行权重分配。当专家数量增加（通常需扩大\(K\)以提升模型能力）时，门控网络面临高维决策问题，易导致训练不稳定或陷入次优解。

    • 门控需要“费力”地从包含混杂信息（共享+所有任务特定） 的专家池中筛选有用信息，增加了学习难度。

为解决上述问题，cite:tang2020progressive 提出提出了CGC（Customized Gate Control）结构，其核心思想是通过硬性结构约束，显式分离共享知识与任务特定知识：

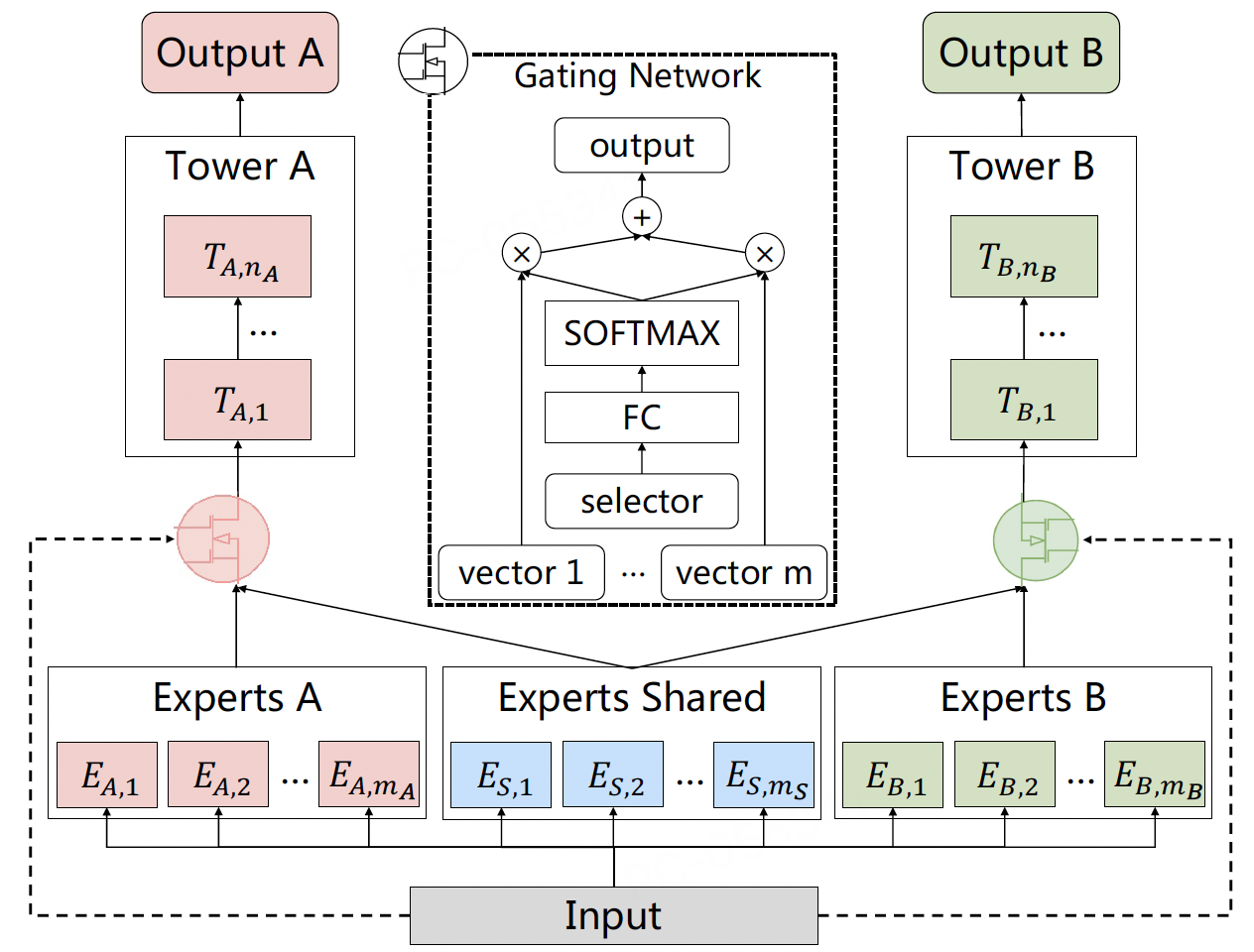
../../_images/cgc.png

图3.4.3 CGC网络结构

专家职责强制分离：

  • 共享专家 (C-Experts)：一组专家仅负责学习所有任务的共性知识。设其数量为\(M\)，输出为\({\mathbf{c}_1, \mathbf{c}_2, ..., \mathbf{c}_M}\)。

  • 任务专家 (T-Experts)：每个任务\(t\)拥有自己专属的专家组，仅负责学习该任务特有的知识或模式。设任务\(t\)的专属专家数量为\(N_t\)，输出为\({\mathbf{t}_t^1, \mathbf{t}_t^2, ..., \mathbf{t}_t^{N_t}}\)。

任务专属门控的输入限制：

  • 任务\(t\)的门控\(g_t\)的输入被严格限制为：共享专家输出 (\({\mathbf{c}k}{k=1}^M\)) + 本任务专属专家输出 (\({\mathbf{t}t^j}{j=1}^{N_t}\))。

  • 物理切断干扰路径：任务\(t\)的门控完全无法访问其他任务\(s (s \neq t)\)的专属专家\({\mathbf{t}_s^j}\)。同样，任务\(s\)的梯度绝不会更新任务\(t\)的专属专家参数。

CGC门控的计算如下：

(3.4.3)\[g_t(\mathbf{x}) = \text{softmax}\Big(\mathbf{W}_t \cdot \mathbf{x} + \mathbf{b}_t\Big) \quad\]
(3.4.4)\[\mathbf{h}_t = \sum_{k=1}^{M} g_{t,k} \cdot \mathbf{c}_k + \sum_{j=1}^{N_t} g_{t, M+j} \cdot \mathbf{t}_t^j\]
(3.4.5)\[\hat{y}_t = f_t(\mathbf{h}_t)\]

其中：

  • \(\mathbf{W}_t, \mathbf{b}_t\)：任务\(t\)门控的参数。

  • \(g_{t,k}\)：分配给第\(k\)个共享专家的权重。

  • \(g_{t, M+j}\)：分配给任务\(t\)第\(j\)个专属专家的权重。

CGC核心代码为：

def cgc_net(
        input_list,
        task_num,
        task_expert_num,
        shared_expert_num,
        task_expert_dnn_units,
        shared_expert_dnn_units,
        task_gate_dnn_units,
        shared_gate_dnn_units,
        leval_name=None,
        is_last=False):
    """CGC（共享专家 + 任务门控）核心结构（简化版）
    - 每个任务：拥有若干 Task-Experts；
    - 全局：拥有若干 Shared-Experts；
    - 每个任务 Gate 产生 softmax 权重，对其 Task-Experts 与 Shared-Experts 加权融合；
    - 若非最后一层：再用 Shared-Gate 融合所有任务的 Task-Experts 与 Shared-Experts，供下一层共享使用。
    input_list：为方便处理，给每个任务复制一份相同输入，最后一个为共享输入。
    """

    # 任务专家：每个任务创建 task_expert_num 个专家
    task_expert_list = []
    for i in range(task_num):
        task_expert_list.append([
            DNNs(task_expert_dnn_units, name=f"{leval_name}_task_{i}_expert_{j}")(input_list[i])
            for j in range(task_expert_num)
        ])

    # 共享专家：创建 shared_expert_num 个专家（共享输入使用 input_list[-1]）
    shared_expert_list = [
        DNNs(shared_expert_dnn_units, name=f"{leval_name}_shared_expert_{i}")(input_list[-1])
        for i in range(shared_expert_num)
    ]

    # 任务门控与融合：对当前任务的（Task + Shared）专家集合进行 softmax 加权求和
    cgc_outputs = []
    fusion_expert_num = task_expert_num + shared_expert_num
    for i in range(task_num):
        cur_experts = task_expert_list[i] + shared_expert_list
        experts = tf.keras.layers.Lambda(lambda xs: tf.stack(xs, axis=1))(cur_experts)  # [B, E, D]

        gate_hidden = DNNs(task_gate_dnn_units, name=f"{leval_name}_task_{i}_gate")(input_list[i])
        gate_weights = tf.keras.layers.Dense(fusion_expert_num, use_bias=False, activation='softmax')(gate_hidden)  # [B, E]

        # 加权融合：einsum('be,bed->bd') == sum_e w_e * expert_e
        fused = tf.keras.layers.Lambda(lambda x: tf.einsum('be,bed->bd', x[0], x[1]))([gate_weights, experts])
        cgc_outputs.append(fused)

    # 若非最后一层：共享门控融合所有任务专家与共享专家，作为下一层共享输入
    if not is_last:
        # 展平所有任务的专家 + 共享专家
        all_task_experts = [e for task in task_expert_list for e in task]
        cur_experts = all_task_experts + shared_expert_list
        experts_all = tf.keras.layers.Lambda(lambda xs: tf.stack(xs, axis=1))(cur_experts)  # [B, E_all, D]
        cur_expert_num = len(cur_experts)

        shared_gate_hidden = DNNs(shared_gate_dnn_units, name=f"{leval_name}_shared_gate")(input_list[-1])
        shared_gate_weights = tf.keras.layers.Dense(cur_expert_num, use_bias=False, activation='softmax')(shared_gate_hidden)  # [B, E_all]
        shared_fused = tf.keras.layers.Lambda(lambda x: tf.einsum('be,bed->bd', x[0], x[1]))([shared_gate_weights, experts_all])
        cgc_outputs.append(shared_fused)

    return cgc_outputs

CGC解决了知识分离的核心问题，但其本质是单层结构，表征学习深度有限。受深度神经网络逐层抽象特征的启发，PLE (Progressive Layered Extraction) 将多个CGC单元纵向堆叠，形成深层架构，实现渐进式知识提取与融合。

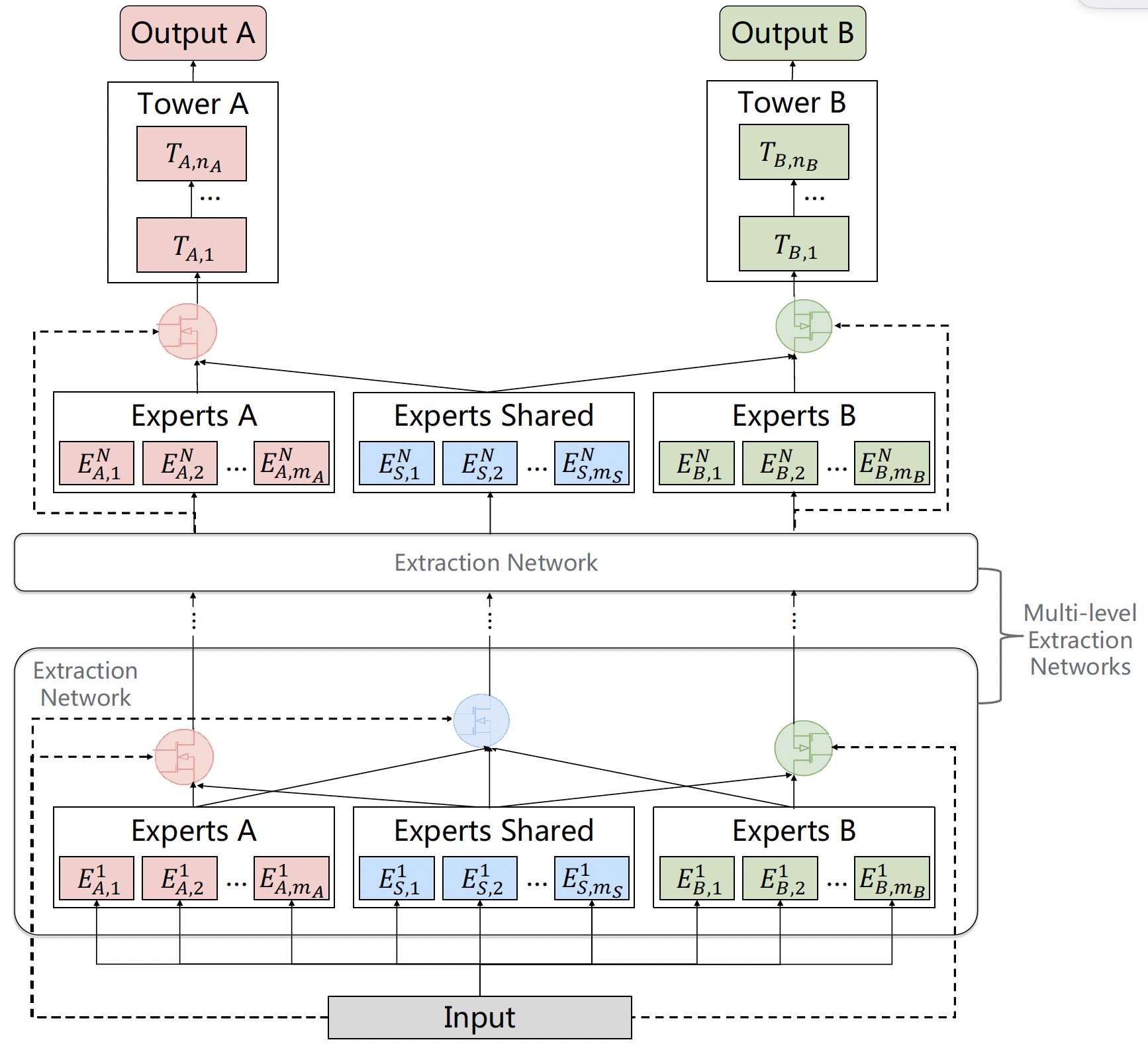
../../_images/ple.png

图3.4.4 PLE网络结构

  • 第1层 (输入层 CGC)：

    • 输入：原始特征 \(\mathbf{x}\)。

    • 结构：一个标准的CGC模块（包含 \(M^{(1)}\)个C-Experts, 每个任务\(t\)有 \(N_t^{(1)}\)个T-Experts, 以及对应的门控 \(g_t^{(1)}\)）。

    • 输出：每个任务获得初步融合表示 \(\mathbf{h}_t^{(1)}\)（或更常见的是，该层所有专家（C+T）的输出被拼接/收集起来作为下一层输入）。

  • 第\(l\)层 (\(l \geq 2\)) CGC：

    • 输入关键点：第\(l\)层的输入是第\(l-1\)层所有专家（包括所有C-Experts和所有任务的T-Experts）的输出。设第\(l-1\)层总专家数为 \(E^{(l-1)}\)，则输入向量维度相应增加。

    • 结构：一个新的CGC模块（包含 \(M^{(l)}\)个C-Experts, 每个任务\(t\)有 \(N_t^{(l)}\)个T-Experts, 以及门控 \(g_t^{(l)}\)）。

    • 处理：在本层输入特征（即上一层更丰富的表征）上，再次进行显式的知识分离（新的C-Experts学习更深层共享模式，新的T-Experts学习更深层任务特定模式）和融合（通过新的门控）。

    • 输出：任务\(t\)的当前层表示 \(\mathbf{h}_t^{(l)}\) 或收集所有专家输出。

  • 输出层 (第\(L\)层)：

    • 最后一层(\(L\))各任务的门控输出 \(\mathbf{h}_t^{(L)}\) 送入各自的任务专属塔网络（Tower）\(f_t\)，得到最终预测 \(\hat{y}_t = f_t(\mathbf{h}_t^{(L)})\)。

PLE模型的核心代码：

def build_ple_model(
        feature_columns,
        task_name_list,
        ple_level_nums=1,
        task_expert_num=4,
        shared_expert_num=2,
        task_expert_dnn_units=[128, 64],
        shared_expert_dnn_units=[128, 64],
        task_gate_dnn_units=[128, 64],
        shared_gate_dnn_units=[128, 64],
        task_tower_dnn_units=[128, 64],
        ):
    # 1) 输入与嵌入：构建输入层/分组嵌入，拼接为 PLE 的共享输入
    input_layer_dict = build_input_layer(feature_columns)
    group_embedding_feature_dict = build_group_feature_embedding_table_dict(
        feature_columns, input_layer_dict, prefix="embedding/"
    )
    dnn_inputs = concat_group_embedding(group_embedding_feature_dict, 'dnn')

    # 2) 级联 PLE（CGC）层：每层包含“任务专家 + 共享专家 + 门控”，最后一层仅输出任务特征
    task_num = len(task_name_list)
    ple_input_list = [dnn_inputs] * (task_num + 1)  # 前 task_num 为各任务输入，末尾为共享输入
    for i in range(ple_level_nums):
        is_last = (i == ple_level_nums - 1)
        ple_input_list = cgc_net(
            ple_input_list,
            task_num,
            task_expert_num,
            shared_expert_num,
            task_expert_dnn_units,
            shared_expert_dnn_units,
            task_gate_dnn_units,
            shared_gate_dnn_units,
            leval_name=f"cgc_level_{i}",
            is_last=is_last
        )

    # 3) 任务塔与输出：将各任务特征送入塔 DNN，得到每个任务的概率输出
    task_output_list = []
    for i in range(task_num):
        task_logit = DNNs(task_tower_dnn_units + [1])(ple_input_list[i])
        task_prob = PredictLayer(name="task_" + task_name_list[i])(task_logit)
        task_output_list.append(task_prob)

    # 4) 构建模型：输入为所有原始输入层，输出为各任务概率
    model = tf.keras.Model(inputs=list(input_layer_dict.values()), outputs=task_output_list)
    return model

训练和评估

run_experiment('ple')

+----------------+---------------+-----------------+-------------+-----------------+----------------+------------------+--------------+---------------------+--------------------+----------------------+
|   auc_is_click |   auc_is_like |   auc_long_view |   auc_macro |   gauc_is_click |   gauc_is_like |   gauc_long_view |   gauc_macro |   val_user_is_click |   val_user_is_like |   val_user_long_view |
+================+===============+=================+=============+=================+================+==================+==============+=====================+====================+======================+
|         0.5975 |        0.4191 |          0.4474 |       0.488 |           0.574 |         0.4434 |           0.4561 |       0.4912 |                 928 |                530 |                  925 |
+----------------+---------------+-----------------+-------------+-----------------+----------------+------------------+--------------+---------------------+--------------------+----------------------+